Java에서 재귀는 "메서드가 직접 또는 간접적으로 계속 자신(동일한 메서드)을 호출하는 것"으로 정의됩니다. 재귀 함수는 결과에 도달할 때까지 동일한 작업 집합을 계속해서 수행해야 하는 상황에서 사용됩니다. 여러 번의 반복을 수행하며, 반복할 때마다 문제 설명이 점점 더 단순해집니다. 자바의 재귀는 동일한 문제의 더 작은 블록에 대한 솔루션을 기반으로 문제를 해결하는 방법입니다. 무한 가능성 반복의 대부분은 재귀를 통해 해결될 수 있습니다. 재귀는 문을 반복하는 대체 방법이라고 말할 수 있습니다. 재귀함수를 제대로 사용하지 않으면 무한 반복하게 됩니다.
구문:
광고 이 카테고리에서 인기 있는 강좌 JAVA MASTERY - 전문 분야 | 78 코스 시리즈 | 15가지 모의고사returntype methodName()
{
//logic for application
methodName();//recursive call
}무한조건을 멈추려면 다음이 필요합니다.
다음 두 가지 방법으로 재귀 함수를 호출할 수 있습니다.
내부 메소드 몸체에서 동일한 메소드를 호출하는 경우
구문:
returntype methodName()
{
//logic for application
methodName();//recursive call
}예:
숫자의 팩토리얼은 직접 재귀의 예입니다. 재귀의 기본 원리는 복잡한 문제를 더 작은 문제로 분할하여 해결하는 것입니다. 예를 들어 숫자의 계승의 경우 "i-1"의 계승을 알고 있으면 "i"의 계승을 계산합니다.
코드:
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}출력:

다른 메서드에서 메서드를 호출하고 첫 번째 메서드에서 다른 메서드를 호출하면 그 반대도 마찬가지입니다.
구문:
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}예:
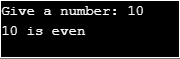
간접 재귀를 보여주기 위해 주어진 입력에서 주어진 숫자가 짝수인지 홀수인지 알아내는 데 사용되는 다음 프로그램을 사용합니다.
코드:
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}출력:
재귀 방법을 사용하여 문제를 해결하는 몇 가지 예는 다음과 같습니다.
숫자3=숫자1+숫자2인 경우 "n"개의 숫자 집합이 피보나치 수열에 있다고 합니다. 즉, 각 숫자는 이전 두 숫자의 합입니다. 따라서 시퀀스는 항상 0과 1과 같은 처음 두 숫자로 시작합니다. 세 번째 숫자는 0과 1의 합으로 1이 되고, 네 번째 숫자는 1과 1을 더하여 2가 되며 시퀀스가 계속됩니다.
피보나치 수열을 생성하려면 Java에서 다음 코드를 확인하세요.
코드:
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}출력:

여기서 처음 두 숫자는 0과 1로 초기화되어 인쇄됩니다. 변수 "num1", "num2" 및 "num3"은 필요한 시퀀스를 생성하는 데 사용됩니다. 변수 “num3”은 “num1”과 “num2”를 더하여 얻어지며, 코드에서 보이는 것처럼 셔플링을 통해 숫자가 왼쪽으로 한 자리 이동됩니다. 여기서 "피보나치" 함수가 재귀적으로 호출되는데, 매 반복마다 "n"의 값이 1씩 감소합니다. 따라서 "n"이 값 0에 도달하는 즉시 재귀가 종료됩니다.
이것은 3개의 극과 다양한 크기의 "n"개 디스크가 있는 고전적인 수학 문제입니다. 퍼즐은 다음과 같습니다:
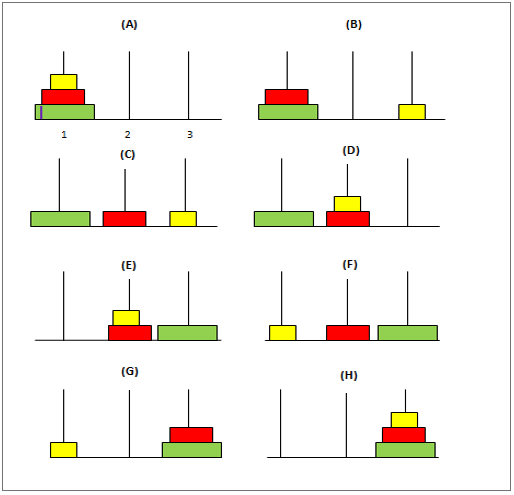
처음에는 첫 번째 폴에서 가장 큰 디스크가 아래쪽에 있고 가장 작은 디스크가 폴 위쪽에 오도록 디스크를 배열합니다. 목표는 디스크를 첫 번째 극과 동일한 위치에 유지하면서 첫 번째 극에서 세 번째 극으로 디스크를 이동하는 것입니다. 다음은 이러한 디스크를 이동할 때 염두에 두어야 할 몇 가지 조건입니다.
다음은 퍼즐을 푸는 데 사용할 수 있는 Java 코드입니다.
코드:
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}출력:
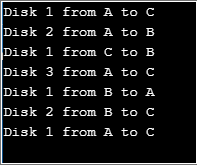
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Code:
package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}Output:
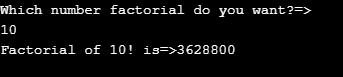
Code:
import java.util.Scanner;
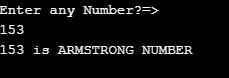
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}Output:
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
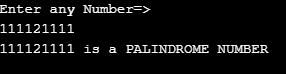
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
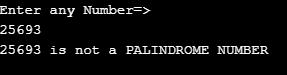
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}Output:
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
위 내용은 Java의 재귀의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!