WeightedGraph 클래스는 AbstractGraph를 확장합니다.
이전 장에서는 그래프 모델링을 위한 Graph 인터페이스, AbstractGraph 클래스, UnweightedGraph 클래스를 설계했습니다. 이 패턴에 따라 우리는 아래 그림과 같이 AbstractGraph의 하위 클래스로 WeightedGraph를 디자인합니다.

WeightedGraph는 구체적인 WeightedGraph 인스턴스를 생성하기 위한 5개의 생성자를 사용하여 AbstractGraph를 확장합니다. WeightedGraph는 AbstractGraph에서 모든 메서드를 상속하고, clear 및 addVertex 메서드를 재정의하고, 가중치 간선을 추가하고 최소 스패닝 트리를 얻고 모든 단일 소스 최단 경로를 찾는 새로운 방법도 도입합니다. 최소 스패닝 트리와 최단 경로는 각각 최소 스패닝 트리와 최단 경로 섹션에서 소개됩니다. 아래 코드는
WeightedGraph를 구현합니다. 가장자리 인접 목록(38-63행)은 정점에 대한 인접한 가장자리를 저장하기 위해 내부적으로 사용됩니다. WeightedGraph가 구성되면 가장자리 인접 목록이 생성됩니다(47행과 57행). getMinimumSpanningTree()(99~138행) 및 getShortestPath()(156~197행) 메소드는 다음 섹션에서 소개됩니다.
package demo;
import java.util.*;
public class WeightedGraph<V> extends AbstractGraph<V> {
/** Construct an empty */
public WeightedGraph() {}
/** Construct a WeightedGraph from vertices and edged in arrays */
public WeightedGraph(V[] vertices, int[][] edges) {
createWeightedGraph(java.util.Arrays.asList(vertices), edges);
}
/** Construct a WeightedGraph from vertices and edges in list */
public WeightedGraph(int[][] edges, int numberOfVertices) {
List<V> vertices = new ArrayList<>();
for (int i = 0; i < numberOfVertices; i++)
vertices.add((V)(new Integer(i)));
createWeightedGraph(vertices, edges);
}
/** Construct a WeightedGraph for vertices 0, 1, 2 and edge list */
public WeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
createWeightedGraph(vertices, edges);
}
/** Construct a WeightedGraph from vertices 0, 1, and edge array */
public WeightedGraph(List<WeightedEdge> edges, int numberOfVertices) {
List<V> vertices = new ArrayList<>();
for (int i = 0; i < numberOfVertices; i++)
vertices.add((V)(new Integer(i)));
createWeightedGraph(vertices, edges);
}
/** Create adjacency lists from edge arrays */
private void createWeightedGraph(List<V> vertices, int[][] edges) {
this.vertices = vertices;
for (int i = 0; i < vertices.size(); i++) {
neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
}
for (int i = 0; i < edges.length; i++) {
neighbors.get(edges[i][0]).add(new WeightedEdge(edges[i][0], edges[i][1], edges[i][2]));
}
}
/** Create adjacency lists from edge lists */
private void createWeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
this.vertices = vertices;
for (int i = 0; i < vertices.size(); i++) {
neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
}
for (WeightedEdge edge: edges) {
neighbors.get(edge.u).add(edge); // Add an edge into the list
}
}
/** Return the weight on the edge (u, v) */
public double getWeight(int u, int v) throws Exception {
for (Edge edge : neighbors.get(u)) {
if (edge.v == v) {
return ((WeightedEdge)edge).weight;
}
}
throw new Exception("Edge does not exit");
}
/** Display edges with weights */
public void printWeightedEdges() {
for (int i = 0; i < getSize(); i++) {
System.out.print(getVertex(i) + " (" + i + "): ");
for (Edge edge : neighbors.get(i)) {
System.out.print("(" + edge.u + ", " + edge.v + ", " + ((WeightedEdge)edge).weight + ") ");
}
System.out.println();
}
}
/** Add edges to the weighted graph */
public boolean addEdge(int u, int v, double weight) {
return addEdge(new WeightedEdge(u, v, weight));
}
/** Get a minimum spanning tree rooted at vertex 0 */
public MST getMinimumSpanningTree() {
return getMinimumSpanningTree(0);
}
/** Get a minimum spanning tree rooted at a specified vertex */
public MST getMinimumSpanningTree(int startingVertex) {
// cost[v] stores the cost by adding v to the tree
double[] cost = new double[getSize()];
for (int i = 0; i < cost.length; i++) {
cost[i] = Double.POSITIVE_INFINITY; // Initial cost
}
cost[startingVertex] = 0; // Cost of source is 0
int[] parent = new int[getSize()]; // Parent of a vertex
parent[startingVertex] = -1; // startingVertex is the root
double totalWeight = 0; // Total weight of the tree thus far
List<Integer> T = new ArrayList<>();
// Expand T
while (T.size() < getSize()) {
// Find smallest cost v in V - T
int u = -1; // Vertex to be determined
double currentMinCost = Double.POSITIVE_INFINITY;
for (int i = 0; i < getSize(); i++) {
if (!T.contains(i) && cost[i] < currentMinCost) {
currentMinCost = cost[i];
u = i;
}
}
T.add(u); // Add a new vertex to T
totalWeight += cost[u]; // Add cost[u] to the tree
// Adjust cost[v] for v that is adjacent to u and v in V - T
for (Edge e : neighbors.get(u)) {
if (!T.contains(e.v) && cost[e.v] > ((WeightedEdge)e).weight) {
cost[e.v] = ((WeightedEdge)e).weight;
parent[e.v] = u;
}
}
} // End of while
return new MST(startingVertex, parent, T, totalWeight);
}
/** MST is an inner class in WeightedGraph */
public class MST extends Tree {
private double totalWeight; // Total weight of all edges in the tree
public MST(int root, int[] parent, List<Integer> searchOrder, double totalWeight) {
super(root, parent, searchOrder);
this.totalWeight = totalWeight;
}
public double getTotalWeight() {
return totalWeight;
}
}
/** Find single source shortest paths */
public ShortestPathTree getShortestPath(int sourceVertex) {
// cost[v] stores the cost of the path from v to the source
double[] cost = new double[getSize()];
for (int i = 0; i < cost.length; i++) {
cost[i] = Double.POSITIVE_INFINITY; // Initial cost set to infinity
}
cost[sourceVertex] = 0; // Cost of source is 0
// parent[v] stores the previous vertex of v in the path
int[] parent = new int[getSize()];
parent[sourceVertex] = -1; // The parent of source is set to -1
// T stores the vertices whose path found so far
List<Integer> T = new ArrayList<>();
// Expand T
while (T.size() < getSize()) {
// Find smallest cost v in V - T
int u = -1; // Vertex to be determined
double currentMinCost = Double.POSITIVE_INFINITY;
for (int i = 0; i < getSize(); i++) {
if (!T.contains(i) && cost[i] < currentMinCost) {
currentMinCost = cost[i];
u = i;
}
}
T.add(u); // Add a new vertex to T
// Adjust cost[v] for v that is adjacent to u and v in V - T
for (Edge e : neighbors.get(u)) {
if (!T.contains(e.v) && cost[e.v] > cost[u] + ((WeightedEdge)e).weight) {
cost[e.v] = cost[u] + ((WeightedEdge)e).weight;
parent[e.v] = u;
}
}
} // End of while
// Create a ShortestPathTree
return new ShortestPathTree(sourceVertex, parent, T, cost);
}
/** ShortestPathTree is an inner class in WeightedGraph */
public class ShortestPathTree extends Tree {
private double[] cost; // cost[v] is the cost from v to source
/** Construct a path */
public ShortestPathTree(int source, int[] parent, List<Integer> searchOrder, double[] cost) {
super(source, parent, searchOrder);
this.cost = cost;
}
/** Return the cost for a path from the root to vertex v */
public double getCost(int v) {
return cost[v];
}
/** Print paths from all vertices to the source */
public void printAllPaths() {
System.out.println("All shortest paths from " + vertices.get(getRoot()) + " are:");
for (int i = 0; i < cost.length; i++) {
printPath(i); // Print a path from i to the source
System.out.println("(cost: " + cost[i] + ")"); // Path cost
}
}
}
}
클래스는 AbstractGraph 클래스(3행)를 확장합니다. AbstractGraph의 vertices 및 neighbors 속성은 WeightedGraph.neighbors에 상속되어 목록입니다. 각 요소는 목록이며 가장자리를 포함하는 또 다른 목록입니다. 비가중 그래프의 경우 각 가장자리는 AbstractGraph.Edge의 인스턴스입니다. 가중치 그래프의 경우 각 가장자리는 WeightedEdge의 인스턴스입니다. WeightedEdge는 Edge의 하위 유형입니다. 따라서 가중치 그래프(47행)를 위해 neighbors.get(i)에 가중치 간선을 추가할 수 있습니다. 아래 코드는 아래 그림에 대한 그래프와 아래 그림 a에 대한 또 다른 그래프를 생성하는 테스트 프로그램을 제공합니다.
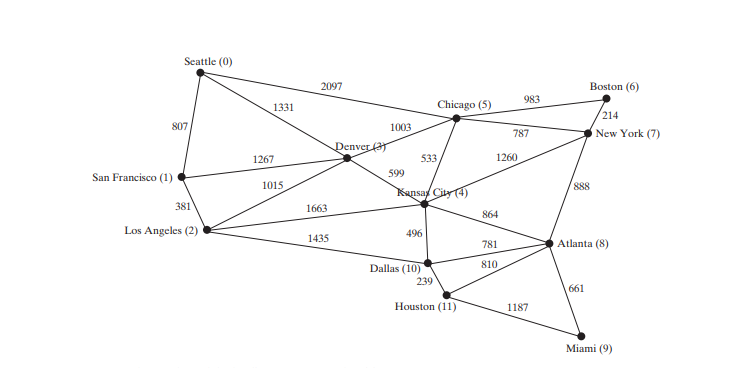
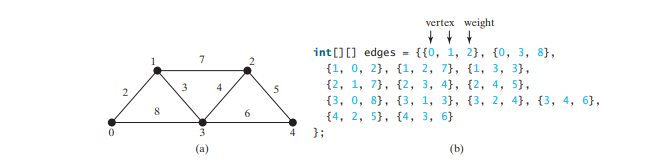
package demo;
public class TestWeightedGraph {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
int[][] edges = {
{0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
{1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
{2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
{3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
{4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
{5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
{6, 5, 983}, {6, 7, 214},
{7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
{8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
{9, 8, 661}, {9, 11, 1187},
{10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
{11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
};
WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
System.out.println("The number of vertices in graph1: " + graph1.getSize());
System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
System.out.println("The edges for graph1:");
graph1.printWeightedEdges();
edges = new int[][] {
{0, 1, 2}, {0, 3, 8},
{1, 0, 2}, {1, 2, 7}, {1, 3, 3},
{2, 1, 7}, {2, 3, 4}, {2, 4, 5},
{3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
{4, 2, 5}, {4, 3, 6}
};
WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
System.out.println("\nThe edges for graph2:");
graph2.printWeightedEdges();
}
}
마이애미의 지수는 9입니다
graph1의 가장자리:
정점 0: (0, 1, 807) (0, 3, 1331) (0, 5, 2097)
정점 1: (1, 2, 381) (1, 0, 807) (1, 3, 1267)
정점 2: (2, 1, 381) (2, 3, 1015) (2, 4, 1663) (2, 10, 1435)
정점 3: (3, 4, 599) (3, 5, 1003) (3, 1, 1267)
(3, 0, 1331) (3, 2, 1015)
정점 4: (4, 10, 496) (4, 8, 864) (4, 5, 533) (4, 2, 1663)
(4, 7, 1260) (4, 3, 599)
정점 5: (5, 4, 533) (5, 7, 787) (5, 3, 1003)
(5, 0, 2097) (5, 6, 983)
정점 6: (6, 7, 214) (6, 5, 983)
정점 7: (7, 6, 214) (7, 8, 888) (7, 5, 787) (7, 4, 1260)
정점 8: (8, 9, 661) (8, 10, 781) (8, 4, 864)
(8, 7, 888) (8, 11, 810)
정점 9: (9, 8, 661) (9, 11, 1187)
정점 10: (10, 11, 239) (10, 4, 496) (10, 8, 781) (10, 2, 1435)
정점 11: (11, 10, 239) (11, 9, 1187) (11, 8, 810)
graph2의 가장자리:
정점 1: (1, 0, 2) (1, 2, 7) (1, 3, 3)
정점 2: (2, 3, 4) (2, 1, 7) (2, 4, 5)
정점 3: (3, 1, 3) (3, 4, 6) (3, 2, 4) (3, 0, 8)
정점 4: (4, 2, 5) (4, 3, 6)
프로그램은 위 그림의 3~27행에 있는 그래프에 대한 graph1을 생성합니다. graph1의 정점은 3~5행에 정의되어 있습니다. graph1의 모서리는 7~24행에 정의되어 있습니다. 모서리는 2차원 배열을 사용하여 표현됩니다. 배열의 각 행 i에 대해 edges[i][0] 및 edges[i][1]은 정점 edges[i]에 모서리가 있음을 나타냅니다. [0]에서 정점 edges[i][1]으로, 가장자리의 가중치는 edges[i][2]입니다. 예를 들어, {0, 1, 807}(8번째 줄)은 정점 0(edges[ 0][0])를 정점 1(가장자리[0][1])에 가중치 807(가장자리[0] 포함 [2]). {0, 5, 2097}(라인 8)은 정점 0(edges[2][의 가장자리를 나타냅니다. 0])를 정점 5(가장자리[2][1])에 가중치 2097(가장자리[2][2] 포함 ). 35행은 graph1에서 printWeightedEdges() 메서드를 호출하여 graph1의 모든 가장자리를 표시합니다.
프로그램은 37~44행에서 위 그림 a의 그래프에 대한 graph2의 모서리를 생성합니다. 46행은 graph2에서 printWeightedEdges() 메서드를 호출하여 graph2의 모든 가장자리를 표시합니다.
위 내용은 WeightedGraph 클래스의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!