배치, 미니 배치 및 확률적 경사하강법

커피 한잔 사주세요😄

*메모:

• 내 게시물에서는 PyTorch의 DataLoader()를 사용한 Batch, Mini-Batch 및 Stochastic Gradient Descent에 대해 설명합니다.
• 내 게시물에서는 PyTorch에서 DataLoader()가 없는 Batch Gradient Descent에 대해 설명합니다.
• 내 게시물에서는 PyTorch의 최적화 프로그램에 대해 설명합니다.

배치 경사하강법(BGD), 미니배치 경사하강법(MBGD), 확률적 경사하강법(SGD)이 있는데 데이터세트에서 데이터를 가져오는 방법으로 경사하강을 수행하는 방법입니다. Adam(), SGD(), RMSprop(), Adadelta(), Adagrad() 등과 같은 최적화 프로그램 파이토치.

*메모:

• PyTorch의 SGD()는 특별한 기능(CGD)이 없는 기본적인 경사하강법일 뿐이며 확률적 경사하강법(SGD)은 아닙니다.
• 예를 들어 아래 방법을 사용하면 BGD, MBGD 또는 SGD Adam을 Adam()으로, CGD를 SGD()로, RMSprop을 RMSprop()로, Adadelta를 Adadelta()로, Adagrad를 Adagrad()로 유연하게 수행할 수 있습니다. PyTorch에서 등등.
• 기본적으로 BGD, MBGD 또는 SGD는 DataLoader()를 사용하여 섞인 데이터세트로 수행됩니다. *메모:
  • 데이터세트를 섞으면 과적합이 완화됩니다. *기본적으로 열차 데이터만 셔플되므로 테스트 데이터는 셔플되지 않습니다.
  • 내 게시물에서는 Overfitting과 Underfitting에 대해 설명합니다.

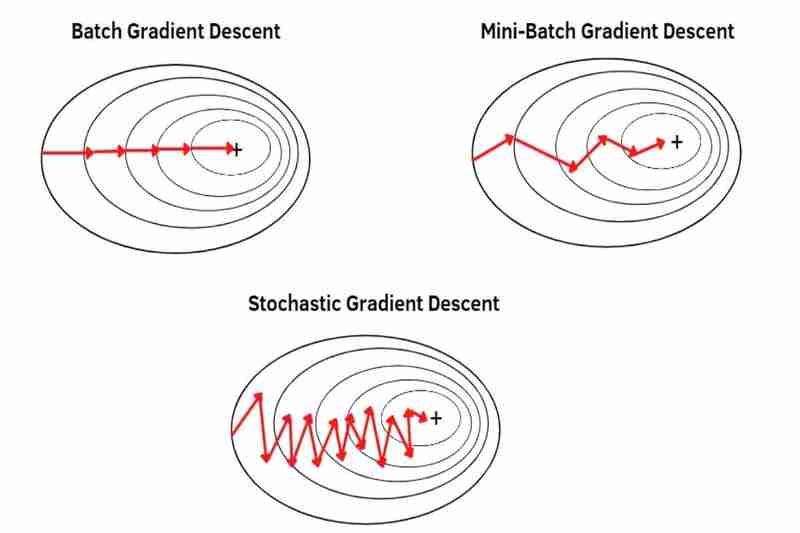
(1) 배치 경사하강법(BGD):

• 한 에포크에서 한 단계만 거치면서 전체 데이터세트에 대해 경사하강법을 수행할 수 있습니다. 예를 들어 전체 데이터세트에 100개의 샘플(1x100)이 있는 경우 경사하강법은 한 에포크에 한 번만 발생합니다. 이는 모델의 매개변수가 한 에포크에 한 번만 업데이트된다는 의미입니다.
• 전체 데이터 세트의 평균을 사용하므로 각 샘플은 MBGD 및 SGD보다 덜 눈에 띕니다(덜 강조됨). 결과적으로 수렴은 MBGD 및 SGD보다 안정적이고(변동이 적음) MBGD 및 SGD보다 잡음(잡음 데이터)이 더 강하여 MBGD 및 SGD보다 오버슈팅이 적고 다음과 같은 경우 MBGD 및 SGD보다 더 정확한 모델을 생성합니다. 로컬 최소점에 갇히지는 않지만 BGD는 수렴이 더 안정적이기 때문에 MBGD 및 SGD보다 로컬 최소점이나 안장점을 덜 쉽게 탈출합니다. 앞에서 말했듯이 BGD는 MBGD 및 SGD보다 변동하며 BGD는 이전에 말했듯이 MBGD 및 SGD보다 각 샘플이 덜 눈에 띄기 때문에(덜 강조됨) MBGD 및 SGD보다 과적합을 더 쉽게 유발합니다. *메모:
  • 수렴은 경사하강법을 통해 초기 가중치가 함수의 전역 최소값 쪽으로 이동하는 것을 의미합니다.
  • 노이즈(noisy data)는 이상값, 이상치 또는 때로는 중복된 데이터를 의미합니다.
  • 오버슈팅은 함수의 전역 최소값을 뛰어넘는 것을 의미합니다.
• 의 장점:
  • MBGD와 SGD보다 수렴이 더 안정적입니다(변동이 적습니다).
  • MBGD, SGD에 비해 노이즈(노이즈 데이터)에 강합니다.
  • MBGD, SGD에 비해 오버슈팅 발생이 적습니다.
  • 로컬 최소값에 갇히지 않으면 MBGD 및 SGD보다 더 정확한 모델을 생성합니다.
• 의 단점:
  • 온라인 학습과 같은 대규모 데이터 세트에는 메모리가 많이 필요하고 수렴 속도가 느려지기 때문에 좋지 않습니다. *온라인 학습은 모델이 실시간으로 데이터 세트 스트림에서 점진적으로 학습하는 방식입니다.
  • 모델을 업데이트하려면 전체 데이터 세트를 다시 준비해야 합니다.
  • MBGD 및 SGD보다 로컬 최소점이나 안장점을 덜 쉽게 탈출합니다.
  • MBGD 및 SGD보다 과적합이 더 쉽게 발생합니다.

(2) 미니 배치 경사하강법(MBGD):

• 분할 데이터세트(전체 데이터세트의 작은 배치)를 사용하여 하나의 작은 배치씩 하나의 작은 배치로 경사하강법을 수행할 수 있으며, 한 에포크에서 전체 데이터세트의 작은 배치와 동일한 수의 단계를 수행할 수 있습니다. 예를 들어, 100개의 샘플(1x100)이 있는 전체 데이터 세트가 5개의 작은 배치(5x20)로 분할된 다음 경사하강법이 한 에포크에 5번 발생합니다. 이는 모델의 매개변수가 한 에포크에 5번 업데이트된다는 의미입니다.

• 전체 데이터 세트에서 분할된 각 소규모 배치의 평균을 사용하므로 각 샘플이 BDG보다 더 눈에 띕니다(더 강조). *전체 데이터 세트를 더 작은 배치로 분할하면 각 샘플이 더욱 눈에 띄게 될 수 있습니다(점점 더 강조됨). 결과적으로 수렴은 BGD보다 덜 안정적이고(더 변동적) BGD보다 잡음(잡음이 많은 데이터)이 덜 강하여 BGD보다 오버슈팅이 더 많이 발생하고 로컬 최소값에 걸리지 않더라도 BGD보다 덜 정확한 모델을 생성하지만 MBGD는 이전에 말했듯이 수렴이 BGD보다 덜 안정적이고(더 변동성이 높음) MBGD가 과적합을 덜 쉽게 유발하기 때문에 BGD보다 로컬 최소점 또는 안장점을 더 쉽게 탈출합니다. 앞서 말했듯 각 샘플이 BGD보다 더 눈에 띄기(더 강조하기) 때문이죠.

• 의 장점:

  • BGD보다 메모리 사용량이 적고 수렴 속도도 BGD보다 덜 느리기 때문에 BGD보다 온라인 학습과 같은 대규모 데이터 세트에 더 좋습니다.
  • 모델을 업데이트하려는 경우 전체 데이터세트를 다시 준비할 필요가 없습니다.
  • BGD보다 로컬 최소점이나 안장점을 더 쉽게 탈출합니다.
  • BGD보다 과적합이 덜 발생합니다.

• 의 단점:

  • 수렴은 BGD보다 덜 안정적(더 변동적)입니다.
  • BGD에 비해 노이즈(noisy data)에 덜 강합니다.
  • BGD보다 오버슈팅이 더 많이 발생합니다.
  • 로컬 최소값에 걸리지 않더라도 BGD보다 정확도가 떨어지는 모델을 생성합니다.

(3) 확률적 경사하강법(SGD):

• 한 에포크에서 전체 데이터세트의 샘플과 동일한 단계 수를 사용하여 전체 데이터세트의 모든 단일 샘플에 대해 하나의 샘플씩 경사하강법을 수행할 수 있습니다. 예를 들어, 전체 데이터 세트에 100개의 샘플(1x100)이 있는 경우 경사하강법이 한 에포크에 100번 발생합니다. 이는 모델의 매개변수가 한 에포크에 100번 업데이트된다는 의미입니다.

• 전체 데이터 세트의 모든 단일 샘플 하나의 샘플을 하나의 샘플로 사용하지만 평균은 사용하지 않으므로 각 샘플이 MBGD보다 더 눈에 띕니다(더 강조). 결과적으로 수렴은 MBGD보다 덜 안정적이고(더 변동적) MBGD보다 잡음(잡음이 있는 데이터)이 덜 강하여 MBGD보다 오버슈팅이 더 많이 발생하고 로컬 최소값에 갇히지 않더라도 MBGD보다 덜 정확한 모델을 생성하지만 이전에 말했듯이 SGD는 MBGD보다 수렴이 MBGD보다 덜 안정적이고(더 변동성이 높음) SGD가 과적합을 덜 쉽게 유발하기 때문에 MBGD보다 로컬 최소값 또는 안장점을 더 쉽게 탈출합니다. 앞서 말했듯 MBGD보다 각 샘플이 더 눈에 띄기(더 강조하기) 때문이죠.

• 의 장점:

  • MBGD보다 메모리 사용량이 적고 MBGD보다 수렴 속도가 덜 느리기 때문에 온라인 학습과 같은 대규모 데이터 세트에 MBGD보다 좋습니다.
  • 모델을 업데이트하려는 경우 전체 데이터세트를 다시 준비할 필요가 없습니다.
  • MBGD보다 로컬 최소점이나 안장점을 더 쉽게 탈출합니다.
  • MBGD보다 과적합이 덜 발생합니다.

• 의 단점:

  • 수렴은 MBGD에 비해 덜 안정적(더 변동적)입니다.
  • MBGD에 비해 노이즈(noisy data)에 덜 강합니다.
  • MBGD보다 오버슈팅의 원인이 더 많습니다.
  • 로컬 최소값에 걸리지 않으면 MBGD보다 덜 정확한 모델을 생성합니다.

위 내용은 배치, 미니 배치 및 확률적 경사하강법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!