퀵 정렬(QuickSort) - Java 구현

배경

퀵 정렬은 1960년대 미국의 토니 홀(Tony Hall)이 제안한 정렬 방법이다. 이 정렬 방법은 당시에는 이미 매우 빠른 정렬 방법이었습니다. 그래서 이름을 따서 "퀵 정렬(quick sort)"이라고 부릅니다. 이 알고리즘은 20세기 7대 알고리즘 중 하나이며, 평균 시간 복잡도는 Ο(nlogn)이며, O(nlogn)의 경우 동일한 시간 복잡도를 갖는 다른 정렬 방법보다 실제 연산 속도가 빠릅니다. .

Tony Hall과 빠른 정렬의 배경에 관심이 있는 학생은 다음 소개를 읽어보세요: http://www.nowamagic.net/librarys/veda/detail/2391

정렬 아이디어

퀵 정렬의 아이디어는 생각하기 어렵지만 이해하기는 매우 쉽습니다

그의 아이디어는 다음과 같습니다.

1. 특정 요소가 기본 값입니다(일반적으로 머리 요소 또는 꼬리 요소가 선택됨).

2. 기본 값을 모든 요소와 순서대로 비교합니다. 요소는 비교 결과에 따라 두 개의 대기열 A와 B로 구분됩니다. 하나는 기본 값보다 큰 모든 요소를 ​​포함하고 다른 하나는 기본 값보다 작은 모든 요소를 ​​포함합니다.

3. A를 새 대기열로 사용하고 기본을 다시 선택한 다음 두 개의 작은 대기열로 나눕니다.

4 이런 식으로 각 작은 대기열을 계속해서 무한대로 분할합니다. 두 개의 대기열.

5. 대기열이 압축을 풀 수 없는 조각으로 분할될 때까지(즉, 하나의 요소)

6. 대기열 간의 순서가 고정되어 있기 때문입니다. 이 대기열을 한 번에 결합하면 전체 정렬이 완료됩니다.

(도난방지 연결: 이 글은 http://www.cnblogs.com/jilodream/ 에서 처음 게시되었습니다.)

여기에는 두 가지 핵심 단계가 있습니다.

1 , Value 요소를 선택하고 전체 대기열을 두 개의 하위 대기열로 나눕니다

2. 그런 다음 하위 대기열을 현재 대기열보다 전체 크기가 작은 새 대기열로 재사용합니다. 계산이 완료될 때까지 계산을 수행합니다. 지금까지는 매우 쉽습니다.

이 두 가지 핵심 단계는 빠른 정렬의 고유한 장점을 만듭니다.

1. 하위 대기열로 분할된 요소의 크기를 비교하여 향후 비교 과정에서 이 요소의 비교 범위는 항상 이 하위 대기열에 머물면서 더 이상 불필요한 비교를 하지 마십시오. 이를 통해 초기 비교가 이후 비교에 여전히 큰 영향을 미칠 수 있습니다. 버블 정렬 방법과 유사하게 초기 단계의 많은 비교는 이후 단계에서 거의 영향을 미치지 않습니다. 이는 kmp 알고리즘과 매우 유사하며 초기 비교에서는 최대한 활용해야 합니다.

2. 원래 규모 대기열을 여러 개의 작은 하위 대기열로 분할해야 합니다. (도난 방지 연결: 이 문서는 http://www.cnblogs.com/jilodream에서 처음 게시되었습니다. /) 해결된 문제는 원래 대기열과 동일하지만 규모가 더 작습니다. 그러한 끊임없는 분열은 분열과 정복의 사고방식을 만들어냅니다. 이 아이디어는 배낭 알고리즘과도 일치합니다.

텍스트를 이해하는 데 어려움을 겪는 학생들을 위해 인터넷에서 매우 생생한 이 고전적이고 역동적인 그림을 볼 수 있습니다.

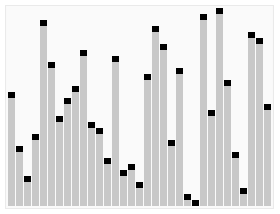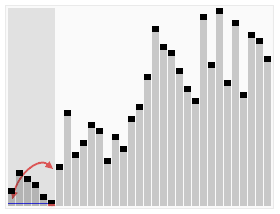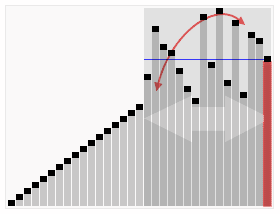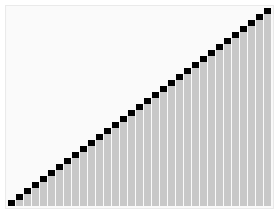
다음 Java 코드로 구현됩니다

import java.util.Arrays;

public class QuickSort
{
    public static void main(String args[])
    {
        QuickSort quicksort = new QuickSort();
        int[] arrays = new int[]
        { 1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19 };
        quicksort.quickSort(arrays);
        System.out.println(Arrays.toString(arrays));
    }
    
    private void quickSort(int[] arrays)
    {
        subQuickSort(arrays, 0, arrays.length - 1);
    }
    
    private void subQuickSort(int[] arrays, int start, int end)
    {
        if (start >= end)
        {
            return;
        }
        int middleIndex = subQuickSortCore(arrays, start, end);
        subQuickSort(arrays, start, middleIndex - 1);
        subQuickSort(arrays, middleIndex + 1, end);
    }
    
    private int subQuickSortCore(int[] arrays, int start, int end)
    {
        int middleValue = arrays[start];
        while (start < end)
        {
            while (arrays[end] >= middleValue && start < end)
            {
                end--;
            }
            arrays[start] = arrays[end];
            while (arrays[start] <= middleValue && start < end)
            {
                start++;
            }
            arrays[end] = arrays[start];
        }
        arrays[start] = middleValue;
        return start;
    }
}