Java 프로그래밍 인터뷰에서 일반적으로 사용되는 상위 10가지 알고리즘 개념 요약
다음은 프로그래밍 인터뷰에서 가장 많이 언급된 알고리즘 관련 개념 10가지입니다. 몇 가지 간단한 예를 통해 이러한 개념을 설명하겠습니다. 이러한 개념을 완전히 익히려면 더 많은 노력이 필요하므로 이 목록은 단지 소개용으로만 작성되었습니다. 이 기사에서는 다음 개념을 포함하여 Java 관점에서 문제를 살펴볼 것입니다.
1. 문자열
IDE에 코드 자동 완성 기능이 없는 경우 다음 사항을 기억해야 합니다. 행동 양식.
toCharArray() // 获得字符串对应的char数组 Arrays.sort() // 数组排序Arrays.toString(char[] a) // 数组转成字符串 charAt(int x) // 获得某个索引处的字符 length() // 字符串长度 length // 数组大小
2. 연결 목록
Java에서 연결 목록의 구현은 매우 간단합니다. 각 노드 노드에는 다음 노드를 가리키는 링크가 있습니다.
class Node {
int val;
Node next;
Node(int x) {
val = x;
next = null;
}
}연결 리스트의 유명한 두 가지 응용 프로그램은 스택과 큐입니다.
스택:
class Stack{
Node top;
public Node peek(){
if(top != null){
return top;
}
return null;
}
public Node pop(){
if(top == null){
return null;
}else{
Node temp = new Node(top.val);
top = top.next;
return temp;
}
}
public void push(Node n){
if(n != null){
n.next = top;
top = n;
}
}
}큐:
class Queue{
Node first, last;
public void enqueue(Node n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public Node dequeue(){
if(first == null){
return null;
}else{
Node temp = new Node(first.val);
first = first.next;
return temp;
}
}
}3. 트리
여기서 트리는 일반적으로 이진 트리를 나타내며 각 노드에는 다음이 포함됩니다. 다음과 같은 왼쪽 자식 노드와 오른쪽 자식 노드:
class TreeNode{
int value;
TreeNode left;
TreeNode right;
}다음은 트리와 관련된 몇 가지 개념입니다.
균형 대 불균형: 균형 이진 트리에서 각 노드는 노드 왼쪽 및 오른쪽 하위 트리의 깊이는 최대 1(1 또는 0)만큼 다릅니다.
완전 이진 트리: 리프 노드를 제외한 모든 노드에는 두 개의 자식이 있습니다.
완전 이진 트리: 다음 속성을 갖는 완전 이진 트리입니다. 모든 리프 노드는 동일한 깊이 또는 동일한 수준에 있으며 각 상위 노드에는 두 개의 하위 노드가 있어야 합니다.
완전 이진 트리: 이진 트리에서는 마지막 레벨을 제외한 모든 레벨이 완전히 채워지며 모든 노드는 가능한 한 왼쪽에 가까워야 합니다.
역자 주: 완전 이진 트리는 막연하게 완전 이진 트리라고도 합니다. 완벽한 이진 트리의 예는 주어진 깊이에서 사람의 조상 그래프입니다. 왜냐하면 모든 사람은 두 명의 생물학적 부모가 있어야 하기 때문입니다. 완전한 이진 트리는 왼쪽으로 기울어진 추가 리프 노드의 수를 가질 수 있는 완벽한 이진 트리로 생각할 수 있습니다. 질문: 완전 이진 트리와 완전 이진 트리의 차이점은 무엇인가요? (참고: http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html)
4. 그래프
그래프 관련 문제는 주로 깊이 우선 탐색에 중점을 둡니다.) 및 너비 우선 찾다.
다음은 그래프 너비 우선 탐색의 간단한 구현입니다.
1) GraphNode 정의
class GraphNode{
int val;
GraphNode next;
GraphNode[] neighbors;
boolean visited;
GraphNode(int x) {
val = x;
}
GraphNode(int x, GraphNode[] n){
val = x;
neighbors = n;
}
public String toString(){
return "value: "+ this.val;
}
}2) 대기열 정의 Queue
class Queue{
GraphNode first, last;
public void enqueue(GraphNode n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public GraphNode dequeue(){
if(first == null){
return null;
}else{
GraphNode temp = new GraphNode(first.val, first.neighbors);
first = first.next;
return temp;
}
}
}3) 대기열 대기열을 사용하여 너비 우선 검색 구현
public class GraphTest {
public static void main(String[] args) {
GraphNode n1 = new GraphNode(1);
GraphNode n2 = new GraphNode(2);
GraphNode n3 = new GraphNode(3);
GraphNode n4 = new GraphNode(4);
GraphNode n5 = new GraphNode(5);
n1.neighbors = new GraphNode[]{n2,n3,n5};
n2.neighbors = new GraphNode[]{n1,n4};
n3.neighbors = new GraphNode[]{n1,n4,n5};
n4.neighbors = new GraphNode[]{n2,n3,n5};
n5.neighbors = new GraphNode[]{n1,n3,n4};
breathFirstSearch(n1, 5);
}
public static void breathFirstSearch(GraphNode root, int x){
if(root.val == x)
System.out.println("find in root");
Queue queue = new Queue();
root.visited = true;
queue.enqueue(root);
while(queue.first != null){
GraphNode c = (GraphNode) queue.dequeue();
for(GraphNode n: c.neighbors){
if(!n.visited){
System.out.print(n + " ");
n.visited = true;
if(n.val == x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}출력:
1 값: 2 값: 3 값: 5 찾기 값: 5
2 값: 4
5 . 정렬
다음은 다양한 정렬 알고리즘의 시간 복잡도입니다. 위키로 이동하여 이러한 알고리즘의 기본 아이디어를 살펴볼 수 있습니다.
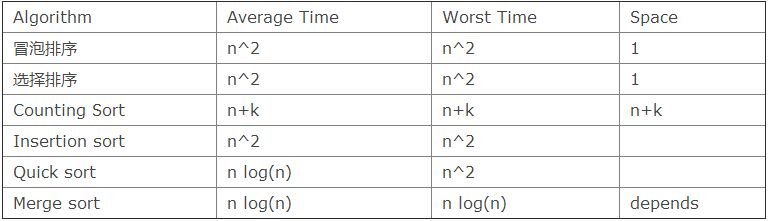
또한 여기에 몇 가지 구현/데모가 있습니다: Counting sort, Mergesort, Quicksort, InsertionSort.
"일반적으로 사용되는 7가지 정렬 알고리즘의 시각적이고 직관적인 경험"
"동영상: 6분 만에 15가지 정렬 알고리즘 시연"
6. >
프로그래머에게 재귀는 내장된 생각이어야 하며, 이는 간단한 예를 통해 설명할 수 있습니다. 질문: n개의 단계가 있는데, 한 번에 1~2단계만 올라갈 수 있나요? 1단계: 처음 n 단계와 첫 n-1 단계 사이의 관계를 찾습니다. n계단을 오르는 방법은 두 가지뿐입니다. n-1계단에서 1계단을 올라가서 거기에 가거나, n-2계단에서 2계단을 올라가서 거기에 가는 것입니다. f(n)이 n번째 단계로 올라가는 방법의 수라면 f(n) = f(n-1) + f(n-2)입니다. 2단계: 시작 조건이 올바른지 확인하세요. f(0) = 0;f(1) = 1;
public static int f(int n){
if(n <= 2) return n;
int x = f(n-1) + f(n-2);
return x;
}f(5) f(4) + f(3) f(3) + f(2) + f(2) + f(1) f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1) f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
public static int f(int n) {
if (n <= 2){
return n;
}
int first = 1, second = 2;
int third = 0;
for (int i = 3; i <= n; i++) {
third = first + second;
first = second;
second = third;
}
return third;
}public static int[] A = new int[100];
public static int f3(int n) {
if (n <= 2)
A[n]= n;
if(A[n] > 0)
return A[n];
else
A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
return A[n];
}
获得给定数字n的第i位:(i从0计数并从右边开始)
public static boolean getBit(int num, int i){
int result = num & (1<<i);
if(result == 0){
return false;
}else{
return true;
}例如,获得数字10的第2位:
i=1, n=10
1<<1= 10
1010&10=10
10 is not 0, so return true;
9. 概率问题
解决概率相关的问题通常需要很好的规划了解问题(formatting the problem),这里刚好有一个这类问题的简单例子:
一个房间里有50个人,那么至少有两个人生日相同的概率是多少?(忽略闰年的事实,也就是一年365天)
计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里,我们可以计算所有人生日都互不相同的概率,也就是:365/365 * 364/365 * 363/365 * … * (365-49)/365,这样至少两个人生日相同的概率就是1 – 这个值。
public static double caculateProbability(int n){
double x = 1;
for(int i=0; i<n; i++){
x *= (365.0-i)/365.0;
}
double pro = Math.round((1-x) * 100);
return pro/100;calculateProbability(50) = 0.97
10. 排列组合
组合和排列的区别在于次序是否关键。
如果你有任何问题请在下面评论。
参考/推荐资料:
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7455
7455
 15
15
 1375
1375
 52
52
 77
77
 11
11
 40
40
 19
19
 14
14
 9
9
 CLIP-BEVFormer: BEVFormer 구조를 명시적으로 감독하여 롱테일 감지 성능을 향상시킵니다.
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: BEVFormer 구조를 명시적으로 감독하여 롱테일 감지 성능을 향상시킵니다.
Mar 26, 2024 pm 12:41 PM
위에 작성 및 저자의 개인적인 이해: 현재 전체 자율주행 시스템에서 인식 모듈은 중요한 역할을 합니다. 자율주행 시스템의 제어 모듈은 적시에 올바른 판단과 행동 결정을 내립니다. 현재 자율주행 기능을 갖춘 자동차에는 일반적으로 서라운드 뷰 카메라 센서, 라이더 센서, 밀리미터파 레이더 센서 등 다양한 데이터 정보 센서가 장착되어 다양한 방식으로 정보를 수집하여 정확한 인식 작업을 수행합니다. 순수 비전을 기반으로 한 BEV 인식 알고리즘은 하드웨어 비용이 저렴하고 배포가 용이하며, 출력 결과를 다양한 다운스트림 작업에 쉽게 적용할 수 있어 업계에서 선호됩니다.
 C++에서 기계 학습 알고리즘 구현: 일반적인 과제 및 솔루션
Jun 03, 2024 pm 01:25 PM
C++에서 기계 학습 알고리즘 구현: 일반적인 과제 및 솔루션
Jun 03, 2024 pm 01:25 PM
C++의 기계 학습 알고리즘이 직면하는 일반적인 과제에는 메모리 관리, 멀티스레딩, 성능 최적화 및 유지 관리 가능성이 포함됩니다. 솔루션에는 스마트 포인터, 최신 스레딩 라이브러리, SIMD 지침 및 타사 라이브러리 사용은 물론 코딩 스타일 지침 준수 및 자동화 도구 사용이 포함됩니다. 실제 사례에서는 Eigen 라이브러리를 사용하여 선형 회귀 알고리즘을 구현하고 메모리를 효과적으로 관리하며 고성능 행렬 연산을 사용하는 방법을 보여줍니다.
 C++sort 함수의 기본 원리와 알고리즘 선택을 살펴보세요.
Apr 02, 2024 pm 05:36 PM
C++sort 함수의 기본 원리와 알고리즘 선택을 살펴보세요.
Apr 02, 2024 pm 05:36 PM
C++정렬 함수의 맨 아래 계층은 병합 정렬을 사용하고 복잡도는 O(nlogn)이며 빠른 정렬, 힙 정렬 및 안정 정렬을 포함한 다양한 정렬 알고리즘 선택을 제공합니다.
 인공지능이 범죄를 예측할 수 있을까? CrimeGPT의 기능 살펴보기
Mar 22, 2024 pm 10:10 PM
인공지능이 범죄를 예측할 수 있을까? CrimeGPT의 기능 살펴보기
Mar 22, 2024 pm 10:10 PM
인공지능(AI)과 법 집행의 융합은 범죄 예방 및 탐지의 새로운 가능성을 열어줍니다. 인공지능의 예측 기능은 범죄 행위를 예측하기 위해 CrimeGPT(범죄 예측 기술)와 같은 시스템에서 널리 사용됩니다. 이 기사에서는 범죄 예측에서 인공 지능의 잠재력, 현재 응용 프로그램, 직면한 과제 및 기술의 가능한 윤리적 영향을 탐구합니다. 인공 지능 및 범죄 예측: 기본 CrimeGPT는 기계 학습 알고리즘을 사용하여 대규모 데이터 세트를 분석하고 범죄가 발생할 가능성이 있는 장소와 시기를 예측할 수 있는 패턴을 식별합니다. 이러한 데이터 세트에는 과거 범죄 통계, 인구 통계 정보, 경제 지표, 날씨 패턴 등이 포함됩니다. 인간 분석가가 놓칠 수 있는 추세를 식별함으로써 인공 지능은 법 집행 기관에 권한을 부여할 수 있습니다.
 탐지 알고리즘 개선: 고해상도 광학 원격탐사 이미지에서 표적 탐지용
Jun 06, 2024 pm 12:33 PM
탐지 알고리즘 개선: 고해상도 광학 원격탐사 이미지에서 표적 탐지용
Jun 06, 2024 pm 12:33 PM
01 전망 요약 현재로서는 탐지 효율성과 탐지 결과 간의 적절한 균형을 이루기가 어렵습니다. 우리는 광학 원격 탐사 이미지에서 표적 감지 네트워크의 효과를 향상시키기 위해 다층 특징 피라미드, 다중 감지 헤드 전략 및 하이브리드 주의 모듈을 사용하여 고해상도 광학 원격 감지 이미지에서 표적 감지를 위한 향상된 YOLOv5 알고리즘을 개발했습니다. SIMD 데이터 세트에 따르면 새로운 알고리즘의 mAP는 YOLOv5보다 2.2%, YOLOX보다 8.48% 우수하여 탐지 결과와 속도 간의 균형이 더 잘 이루어졌습니다. 02 배경 및 동기 원격탐사 기술의 급속한 발전으로 항공기, 자동차, 건물 등 지구 표면의 많은 물체를 묘사하기 위해 고해상도 광학 원격탐사 영상이 활용되고 있다. 원격탐사 이미지 해석에서 물체 감지
 Jiuzhang Yunji DataCanvas 다중 모드 대형 모델 플랫폼에 대한 실습 및 고찰
Oct 20, 2023 am 08:45 AM
Jiuzhang Yunji DataCanvas 다중 모드 대형 모델 플랫폼에 대한 실습 및 고찰
Oct 20, 2023 am 08:45 AM
1. 멀티모달 대형 모델의 역사적 발전 위 사진은 1956년 미국 다트머스 대학에서 열린 최초의 인공지능 워크숍이다. 이 컨퍼런스도 인공지능 개발의 시발점이 된 것으로 평가된다. 상징 논리학의 선구자들(앞줄 중앙에 있는 신경생물학자 피터 밀너를 제외하고). 그러나 이 기호논리 이론은 오랫동안 실현되지 못했고, 1980년대와 1990년대에는 최초의 AI 겨울 시기를 맞이하기도 했습니다. 신경망이 실제로 이러한 논리적 사고를 담고 있다는 사실을 발견한 것은 최근 대규모 언어 모델이 구현된 이후였습니다. 신경생물학자인 Peter Milner의 연구는 인공 신경망의 후속 개발에 영감을 주었으며, 이러한 이유로 그가 참여하도록 초대되었습니다. 이 프로젝트에서.
 58 초상화 플랫폼 구축에 알고리즘 적용
May 09, 2024 am 09:01 AM
58 초상화 플랫폼 구축에 알고리즘 적용
May 09, 2024 am 09:01 AM
1. 58초상화 플랫폼 구축 배경 먼저, 58초상화 플랫폼 구축 배경에 대해 말씀드리겠습니다. 1. 기존 프로파일링 플랫폼의 전통적인 사고로는 더 이상 충분하지 않습니다. 사용자 프로파일링 플랫폼을 구축하려면 여러 비즈니스 라인의 데이터를 통합하여 정확한 사용자 초상화를 구축하는 데이터 웨어하우스 모델링 기능이 필요합니다. 그리고 알고리즘 측면의 기능을 제공해야 하며, 마지막으로 사용자 프로필 데이터를 효율적으로 저장, 쿼리 및 공유하고 프로필 서비스를 제공할 수 있는 데이터 플랫폼 기능도 있어야 합니다. 자체 구축한 비즈니스 프로파일링 플랫폼과 중간 사무실 프로파일링 플랫폼의 주요 차이점은 자체 구축한 프로파일링 플랫폼이 단일 비즈니스 라인에 서비스를 제공하고 필요에 따라 사용자 정의할 수 있다는 것입니다. 모델링하고 보다 일반적인 기능을 제공합니다. 2.58 Zhongtai 초상화 구성 배경의 사용자 초상화
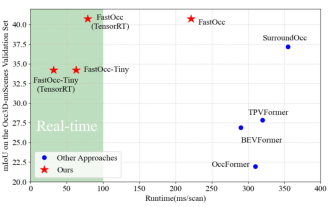 실시간으로 SOTA를 추가하고 급상승하세요! FastOcc: 더 빠른 추론 및 배포 친화적인 Occ 알고리즘이 출시되었습니다!
Mar 14, 2024 pm 11:50 PM
실시간으로 SOTA를 추가하고 급상승하세요! FastOcc: 더 빠른 추론 및 배포 친화적인 Occ 알고리즘이 출시되었습니다!
Mar 14, 2024 pm 11:50 PM
위에 쓴 글 & 저자의 개인적인 이해는 자율주행 시스템에서 인지 작업은 전체 자율주행 시스템의 중요한 구성 요소라는 것입니다. 인지 작업의 주요 목표는 자율주행차가 도로를 주행하는 차량, 길가의 보행자, 주행 중 직면하는 장애물, 도로 위의 교통 표지판 등 주변 환경 요소를 이해하고 인지하여 하류에 도움을 주는 것입니다. 모듈 정확하고 합리적인 결정과 행동을 취하십시오. 자율주행 기능을 갖춘 차량에는 일반적으로 자율주행 차량이 정확하게 인식하고 인식할 수 있도록 서라운드 뷰 카메라 센서, 라이더 센서, 밀리미터파 레이더 센서 등과 같은 다양한 유형의 정보 수집 센서가 장착됩니다. 주변 환경 요소를 이해하여 자율 주행 중에 자율 차량이 올바른 결정을 내릴 수 있도록 합니다. 머리




