피보나치 수열의 일반항을 구현하는 7가지 방법
1: 재귀 구현
f[n]=f[n-1]+f[n-2] 공식을 사용하고, 재귀 종료 조건은 f[1]=1입니다. f[2] =1.
두 번째: 배열 구현
공간 복잡도와 시간 복잡도는 모두 0(n)이고 효율성은 평균이며 재귀보다 빠릅니다.
셋: 벡터
시간 복잡도는 0(n)이고, 시간 복잡도는 0(1)입니다. 물론 벡터가 효율적인지는 알 수 없습니다. 자원을 차지할 자체 속성입니다.
4: Queue
물론 배열보다 피보나치 수열을 구현하는 데에는 대기열이 더 적합합니다. 시간 복잡도와 공간 복잡도는 Vector
다섯 번째: 반복 구현
반복 구현은 시간 복잡도가 0(n)이고 공간 복잡도가 0(1)인 가장 효율적입니다.
식스: 수식 구현
바이두를 검색하다가 피보나치수열에 수식이 있어서 그 수식을 이용해서 계산할 수 있다는 걸 알게 됐어요.
double형의 정확도가 충분하지 않기 때문에 프로그램에서 계산한 결과에 오류가 발생합니다. 수식을 확장하여 계산하면 결과가 정확해집니다.
완전한 구현 코드는 다음과 같습니다. #include "iostream"
#include "queue"
#include "cmath"
using namespace std;
int fib1(int index) //递归实现
{
if(index<1)
{
return -1;
}
if(index==1 || index==2)
return 1;
return fib1(index-1)+fib1(index-2);
}
int fib2(int index) //数组实现
{
if(index<1)
{
return -1;
}
if(index<3)
{
return 1;
}
int *a=new int[index];
a[0]=a[1]=1;
for(int i=2;i<index;i++)
a[i]=a[i-1]+a[i-2];
int m=a[index-1];
delete a; //释放内存空间
return m;
}
int fib3(int index) //借用vector<int>实现
{
if(index<1)
{
return -1;
}
vector<int> a(2,1); //创建一个含有2个元素都为1的向量
a.reserve(3);
for(int i=2;i<index;i++)
{
a.insert(a.begin(),a.at(0)+a.at(1));
a.pop_back();
}
return a.at(0);
}
int fib4(int index) //队列实现
{
if(index<1)
{
return -1;
}
queue<int>q;
q.push(1);
q.push(1);
for(int i=2;i<index;i++)
{
q.push(q.front()+q.back());
q.pop();
}
return q.back();
}
int fib5(int n) //迭代实现
{
int i,a=1,b=1,c=1;
if(n<1)
{
return -1;
}
for(i=2;i<n;i++)
{
c=a+b; //辗转相加法(类似于求最大公约数的辗转相除法)
a=b;
b=c;
}
return c;
}
int fib6(int n)
{
double gh5=sqrt((double)5);
return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}
int main(void)
{
printf("%d\n",fib3(6));
system("pause");
return 0;
}
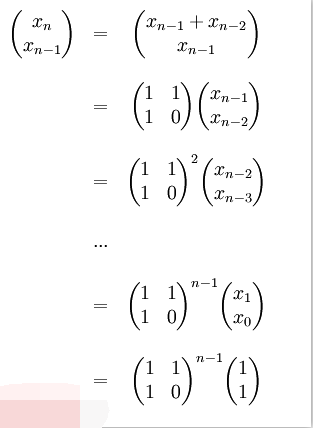
코드는 아래와 같습니다:
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
int tmp[4];
tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
c[0][0]=tmp[0]%mod;
c[0][1]=tmp[1]%mod;
c[1][0]=tmp[2]%mod;
c[1][1]=tmp[3]%mod;
}//计算矩阵乘法,c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
if(n==0)return 0;
else if(n<=2)return 1;//这里表示第0项为0,第1,2项为1
int a[2][2]={{1,1},{1,0}};
int result[2][2]={{1,0},{0,1}};//初始化为单位矩阵
int s;
n-=2;
while(n>0)
{
if(n%2 == 1)
multiply(result,result,a,mod);
multiply(a,a,a,mod);
n /= 2;
}//二分法求矩阵幂
s=(result[0][0]+result[0][1])%mod;//结果
return s;
}int pow(int a,int n)
{
int ans=1;
while(n)
{
if(n&1)
ans*=a;
a*=a;
n>>=1;
}
return ans;
}
핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7456
7456
 15
15
 1376
1376
 52
52
 77
77
 11
11
 44
44
 19
19
 17
17
 10
10
 Laravel의 플래시 세션 데이터로 작업합니다
Mar 12, 2025 pm 05:08 PM
Laravel의 플래시 세션 데이터로 작업합니다
Mar 12, 2025 pm 05:08 PM
Laravel은 직관적 인 플래시 방법을 사용하여 임시 세션 데이터 처리를 단순화합니다. 응용 프로그램에 간단한 메시지, 경고 또는 알림을 표시하는 데 적합합니다. 데이터는 기본적으로 후속 요청에만 지속됩니다. $ 요청-
 PHP의 컬 : REST API에서 PHP Curl Extension 사용 방법
Mar 14, 2025 am 11:42 AM
PHP의 컬 : REST API에서 PHP Curl Extension 사용 방법
Mar 14, 2025 am 11:42 AM
PHP 클라이언트 URL (CURL) 확장자는 개발자를위한 강력한 도구이며 원격 서버 및 REST API와의 원활한 상호 작용을 가능하게합니다. PHP CURL은 존경받는 다중 프로모토콜 파일 전송 라이브러리 인 Libcurl을 활용하여 효율적인 execu를 용이하게합니다.
 Laravel 테스트에서 단순화 된 HTTP 응답 조롱
Mar 12, 2025 pm 05:09 PM
Laravel 테스트에서 단순화 된 HTTP 응답 조롱
Mar 12, 2025 pm 05:09 PM
Laravel은 간결한 HTTP 응답 시뮬레이션 구문을 제공하여 HTTP 상호 작용 테스트를 단순화합니다. 이 접근법은 테스트 시뮬레이션을보다 직관적으로 만들면서 코드 중복성을 크게 줄입니다. 기본 구현은 다양한 응답 유형 단축키를 제공합니다. Illuminate \ support \ Facades \ http를 사용하십시오. http :: 가짜 ([ 'google.com'=> 'Hello World', 'github.com'=> [ 'foo'=> 'bar'], 'forge.laravel.com'=>
 ALIPAY PHP SDK 전송 오류 : '클래스 부호 데이터를 선언 할 수 없음'의 문제를 해결하는 방법은 무엇입니까?
Apr 01, 2025 am 07:21 AM
ALIPAY PHP SDK 전송 오류 : '클래스 부호 데이터를 선언 할 수 없음'의 문제를 해결하는 방법은 무엇입니까?
Apr 01, 2025 am 07:21 AM
Alipay PHP ...
 Codecanyon에서 12 개의 최고의 PHP 채팅 스크립트
Mar 13, 2025 pm 12:08 PM
Codecanyon에서 12 개의 최고의 PHP 채팅 스크립트
Mar 13, 2025 pm 12:08 PM
고객의 가장 긴급한 문제에 실시간 인스턴트 솔루션을 제공하고 싶습니까? 라이브 채팅을 통해 고객과 실시간 대화를 나누고 문제를 즉시 해결할 수 있습니다. 그것은 당신이 당신의 관습에 더 빠른 서비스를 제공 할 수 있도록합니다.
 PHP에서 늦은 정적 결합의 개념을 설명하십시오.
Mar 21, 2025 pm 01:33 PM
PHP에서 늦은 정적 결합의 개념을 설명하십시오.
Mar 21, 2025 pm 01:33 PM
기사는 PHP 5.3에 도입 된 PHP의 LSB (Late STATIC BING)에 대해 논의하여 정적 방법의 런타임 해상도가보다 유연한 상속을 요구할 수있게한다. LSB의 실제 응용 프로그램 및 잠재적 성능
 프레임 워크 사용자 정의/확장 : 사용자 정의 기능을 추가하는 방법.
Mar 28, 2025 pm 05:12 PM
프레임 워크 사용자 정의/확장 : 사용자 정의 기능을 추가하는 방법.
Mar 28, 2025 pm 05:12 PM
이 기사에서는 프레임 워크에 사용자 정의 기능 추가, 아키텍처 이해, 확장 지점 식별 및 통합 및 디버깅을위한 모범 사례에 중점을 둡니다.
 프레임 워크 보안 기능 : 취약점 보호.
Mar 28, 2025 pm 05:11 PM
프레임 워크 보안 기능 : 취약점 보호.
Mar 28, 2025 pm 05:11 PM
기사는 입력 유효성 검사, 인증 및 정기 업데이트를 포함한 취약점을 방지하기 위해 프레임 워크의 필수 보안 기능을 논의합니다.




