일반적으로 사용되는 검색 데이터 구조 및 알고리즘에 대한 자세한 설명(Python 구현)

1. 기본 개념

검색은 주어진 값을 기준으로 조회 테이블의 주어진 값과 키가 동일한 데이터 요소(또는 레코드)를 결정하는 것입니다.

검색 테이블: 동일한 유형의 데이터 요소(또는 레코드) 모음

키: 데이터 요소에 있는 데이터 항목의 값, 키 값이라고도 합니다.

기본 키: 데이터 요소나 레코드를 고유하게 식별하는 키워드입니다.

조회 테이블은 다음과 같이 나눌 수 있습니다.

정적 검색 테이블: 검색 작업만 수행하는 조회 테이블입니다. 주요 작업은 다음과 같습니다.

"특정" 데이터 요소가 테이블에 있는지 쿼리

"특정" 데이터 요소 및 다양한 속성 검색

동적 검색 테이블: 삽입 또는 삭제 작업은 검색 중에 동시에 수행됩니다.

검색 중 데이터 삽입

검색 중 데이터 삭제

2. 순서가 지정되지 않은 테이블 조회

는 선형 조회입니다. 데이터를 정렬하지 않고 데이터 요소를 순회하는 것입니다.

알고리즘 분석: 가장 좋은 경우는 첫 번째 위치인 O(1)에서 발견되는 것이고, 최악의 경우는 마지막 위치인 O(n)에서 발견되는 것입니다. ); 따라서 평균 검색 횟수는 (n+1)/2입니다. 최종 시간복잡도는 O(n)

# 最基础的遍历无序列表的查找算法
# 时间复杂度O(n)
 
def sequential_search(lis, key):
  length = len(lis)
  for i in range(length):
    if lis[i] == key:
      return i
    else:
      return False
 
 
if __name__ == '__main__':
  LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
  result = sequential_search(LIST, 123)
  print(result)

3. 순서화된 테이블 조회

룩업 테이블의 데이터는 기본 키에 따라 정렬되어야 합니다!

1. 이진 검색

알고리즘의 핵심: 조회 테이블의 중간 요소를 조회 값과 지속적으로 비교하여 테이블 범위를 절반으로 줄입니다.

# 针对有序查找表的二分查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    mid = int((low + high) / 2)
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印折半的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 99)
  print(result)

2. 보간 검색

이진 검색 방법은 이미 매우 훌륭하지만 아직 최적화할 수 있는 영역이 있습니다.

때로는 절반으로 필터링하는 것만으로는 충분하지 않을 때가 있습니다. 매번 데이터의 9/10을 제외하는 것이 더 좋지 않을까요? 이 값을 선택하는 것이 핵심 문제입니다. 보간의 의미는 더 빠른 속도로 줄이는 것입니다.

보간의 핵심은 다음 공식을 사용하는 것입니다:

value = (key - list[low])/(list[high] - list[low])

이진 검색에서 1/2을 대체하려면 이 값을 사용하세요.

위 코드는 바로 사용할 수 있으며, 한 문장만 바꾸면 됩니다.

# 插值查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    # 计算mid值是插值算法的核心代码
    mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low]))
    print("mid=%s, low=%s, high=%s" % (mid, low, high))
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印查找的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 444)
  print(result)

보간 알고리즘의 전체 시간 복잡도는 여전히 O(log(n)) 수준입니다. 장점은 테이블에 많은 양의 데이터가 있고 키워드의 분포가 상대적으로 균일한 조회 테이블의 경우 보간 알고리즘을 사용한 평균 성능이 이진 검색보다 훨씬 좋다는 것입니다. 반대로 분포가 매우 고르지 않은 데이터의 경우 보간 알고리즘이 적합하지 않습니다.

3. 피보나치 검색

보간 알고리즘에서 영감을 받아 피보나치 알고리즘이 발명되었습니다. 검색 횟수가 최소화되도록 감소율을 최적화하는 방법도 핵심입니다.

이미 피보나치 데이터가 포함된 목록이 있다고 가정하고 이 알고리즘을 사용하세요.

F = [1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144,...]

# 斐波那契查找算法
# 时间复杂度O(log(n))
 
def fibonacci_search(lis, key):
  # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。
  F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
     233, 377, 610, 987, 1597, 2584, 4181, 6765,
     10946, 17711, 28657, 46368]
  low = 0
  high = len(lis) - 1
   
  # 为了使得查找表满足斐波那契特性，在表的最后添加几个同样的值
  # 这个值是原查找表的最后那个元素的值
  # 添加的个数由F[k]-1-high决定
  k = 0
  while high > F[k]-1:
    k += 1
  print(k)
  i = high
  while F[k]-1 > i:
    lis.append(lis[high])
    i += 1
  print(lis)
   
  # 算法主逻辑。time用于展示循环的次数。
  time = 0
  while low <= high:
    time += 1
    # 为了防止F列表下标溢出，设置if和else
    if k < 2:
      mid = low
    else:
      mid = low + F[k-1]-1
     
    print("low=%s, mid=%s, high=%s" % (low, mid, high))
    if key < lis[mid]:
      high = mid - 1
      k -= 1
    elif key > lis[mid]:
      low = mid + 1
      k -= 2
    else:
      if mid <= high:
        # 打印查找的次数
        print("times: %s" % time)
        return mid
      else:
        print("times: %s" % time)
        return high
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = fibonacci_search(LIST, 444)
  print(result)

알고리즘 분석: 피보나치 검색의 전체 시간 복잡도도 O(log(n ))입니다. 하지만 평균 성능 측면에서는 이진 검색보다 낫습니다. 하지만 최악의 경우, 예를 들어 키가 1이면 항상 왼쪽 절반 영역에서 검색이 이루어지며 이진 검색보다 효율성이 떨어집니다.

요약: 이진 검색의 중간 연산은 덧셈과 나눗셈이고, 보간 검색은 복잡한 4개의 산술 연산이며, 피보나치 검색은 가장 단순한 덧셈과 뺄셈 연산입니다. 대용량 데이터를 검색할 때 이러한 미묘한 차이가 최종 검색 효율성에 영향을 미칠 수 있습니다. 따라서 정렬된 테이블에 대한 세 가지 검색 방법은 분할 지점 선택에 있어서 본질적으로 다릅니다. 각각은 고유한 장점과 단점이 있으므로 실제 상황에 따라 선택해야 합니다.

4. 선형 인덱스 검색

대량의 정렬되지 않은 데이터에 대해서는 검색 속도를 높이기 위해 일반적으로 인덱스 테이블을 구성합니다.

인덱싱은 키워드를 해당 레코드와 연결하는 프로세스입니다.

인덱스는 여러 개의 인덱스 항목으로 구성되며, 각 인덱스 항목에는 최소한 키워드 및 해당 메모리 내 레코드 위치와 같은 정보가 포함됩니다.

인덱스는 그 구조에 따라 선형 인덱스, 트리 인덱스, 다단계 인덱스로 나눌 수 있습니다.

선형 인덱스: 인덱스 테이블이라고도 하는 선형 구조를 통해 인덱스 항목 컬렉션을 구성합니다.

선형 인덱스는 밀집 인덱스, 블록 인덱스, 역 인덱스로 나눌 수 있습니다.

1. 밀집 인덱스

밀집 인덱스는 온라인을 의미합니다. 성적 색인, 데이터 컬렉션의 각 레코드에 대해 색인 항목이 생성됩니다.

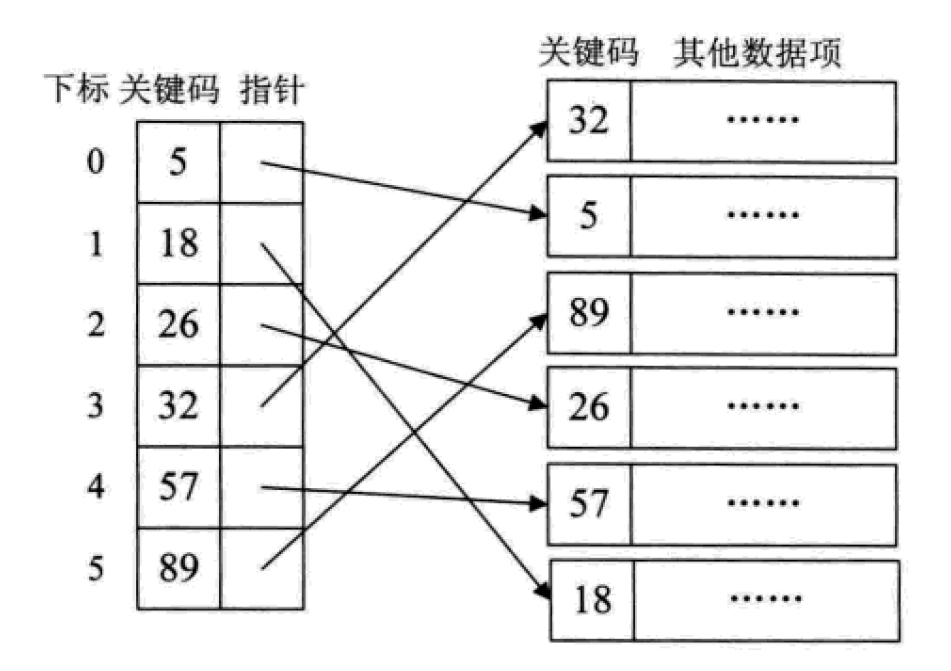
이는 실제로 순서가 없는 집합에 대해 순서가 있는 선형 목록을 만드는 것과 같습니다. 인덱스 항목은 키 코드에 따라 순서대로 배열되어야 합니다.

이 역시 검색 과정에서 필요한 정렬 작업을 미리 해두는 것과 같습니다.

1. 블록 인덱스

는 정렬되지 않은 대량의 데이터 세트를 블록으로 나누어 블록 내에는 무질서가 있고 블록 사이에는 질서가 있습니다.

这其实是有序查找和无序查找的一种中间状态或者说妥协状态。因为数据量过大，建立完整的稠密索引耗时耗力，占用资源过多；但如果不做任何排序或者索引，那么遍历的查找也无法接受，只能折中，做一定程度的排序或索引。

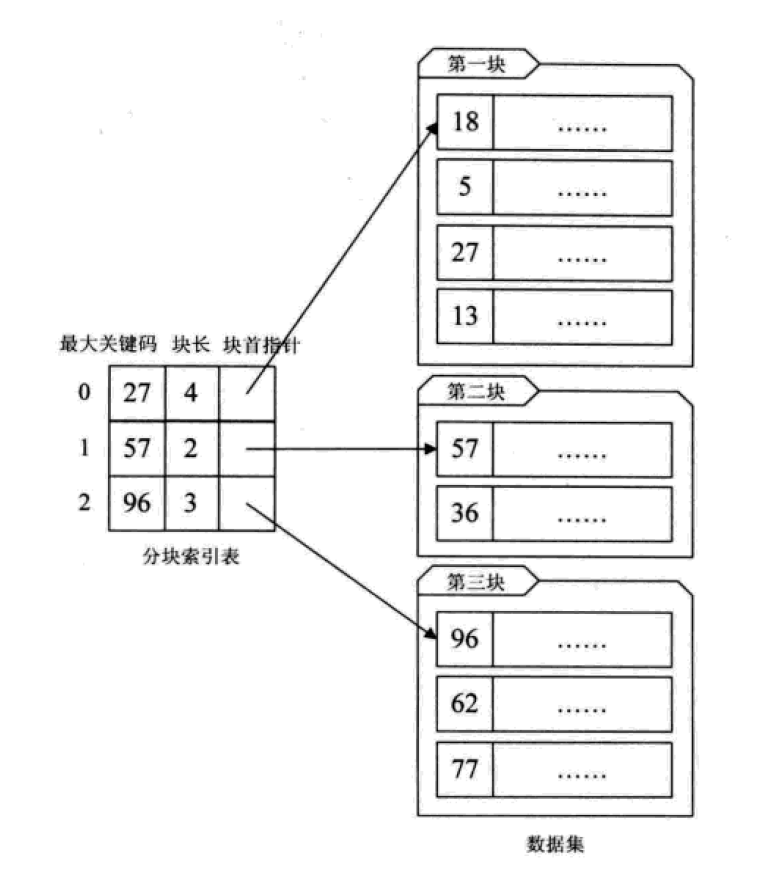
分块索引的效率比遍历查找的O(n)要高一些，但与二分查找的O(logn)还是要差不少。

1.倒排索引

不是由记录来确定属性值，而是由属性值来确定记录的位置，这种被称为倒排索引。其中记录号表存储具有相同次关键字的所有记录的地址或引用（可以是指向记录的指针或该记录的主关键字）。

倒排索引是最基础的搜索引擎索引技术。

五、二叉排序树

二叉排序树又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值均小于它的根结构的值；

若它的右子树不为空，则右子树上所有节点的值均大于它的根结构的值；

它的左、右子树也分别为二叉排序树。

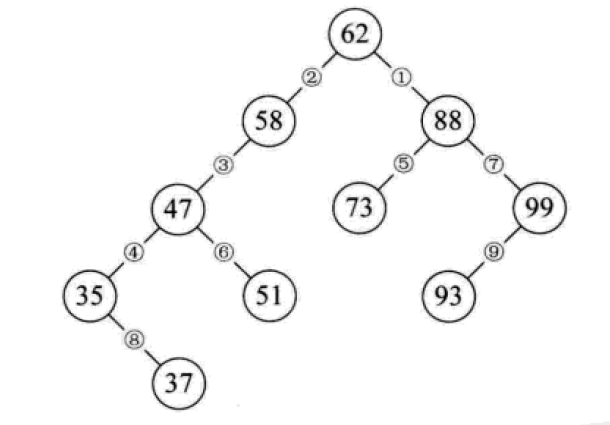
构造一颗二叉排序树的目的，往往不是为了排序，而是为了提高查找和插入删除关键字的速度。

二叉排序树的操作：

1.查找：对比节点的值和关键字，相等则表明找到了；小了则往节点的左子树去找，大了则往右子树去找，这么递归下去，最后返回布尔值或找到的节点。

2.插入：从根节点开始逐个与关键字进行对比，小了去左边，大了去右边，碰到子树为空的情况就将新的节点链接。

3.删除：如果要删除的节点是叶子，直接删；如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；如果同时有左右子树，则可以将二叉排序树进行中序遍历，取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
 
 
class BSTNode:
  """
  定义一个二叉树节点类。
  以讨论算法为主，忽略了一些诸如对数据类型进行判断的问题。
  """
  def __init__(self, data, left=None, right=None):
    """
    初始化
    :param data: 节点储存的数据
    :param left: 节点左子树
    :param right: 节点右子树
    """
    self.data = data
    self.left = left
    self.right = right
 
 
class BinarySortTree:
  """
  基于BSTNode类的二叉排序树。维护一个根节点的指针。
  """
  def __init__(self):
    self._root = None
 
  def is_empty(self):
    return self._root is None
 
  def search(self, key):
    """
    关键码检索
    :param key: 关键码
    :return: 查询节点或None
    """
    bt = self._root
    while bt:
      entry = bt.data
      if key < entry:
        bt = bt.left
      elif key > entry:
        bt = bt.right
      else:
        return entry
    return None
 
  def insert(self, key):
    """
    插入操作
    :param key:关键码
    :return: 布尔值
    """
    bt = self._root
    if not bt:
      self._root = BSTNode(key)
      return
    while True:
      entry = bt.data
      if key < entry:
        if bt.left is None:
          bt.left = BSTNode(key)
          return
        bt = bt.left
      elif key > entry:
        if bt.right is None:
          bt.right = BSTNode(key)
          return
        bt = bt.right
      else:
        bt.data = key
        return
 
  def delete(self, key):
    """
    二叉排序树最复杂的方法
    :param key: 关键码
    :return: 布尔值
    """
    p, q = None, self._root   # 维持p为q的父节点，用于后面的链接操作
    if not q:
      print("空树！")
      return
    while q and q.data != key:
      p = q
      if key < q.data:
        q = q.left
      else:
        q = q.right
      if not q:        # 当树中没有关键码key时，结束退出。
        return
    # 上面已将找到了要删除的节点，用q引用。而p则是q的父节点或者None（q为根节点时）。
    if not q.left:
      if p is None:
        self._root = q.right
      elif q is p.left:
        p.left = q.right
      else:
        p.right = q.right
      return
    # 查找节点q的左子树的最右节点，将q的右子树链接为该节点的右子树
    # 该方法可能会增大树的深度，效率并不算高。可以设计其它的方法。
    r = q.left
    while r.right:
      r = r.right
    r.right = q.right
    if p is None:
      self._root = q.left
    elif p.left is q:
      p.left = q.left
    else:
      p.right = q.left
 
  def __iter__(self):
    """
    实现二叉树的中序遍历算法,
    展示我们创建的二叉排序树.
    直接使用python内置的列表作为一个栈。
    :return: data
    """
    stack = []
    node = self._root
    while node or stack:
      while node:
        stack.append(node)
        node = node.left
      node = stack.pop()
      yield node.data
      node = node.right
 
 
if __name__ == &#39;__main__&#39;:
  lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
  bs_tree = BinarySortTree()
  for i in range(len(lis)):
    bs_tree.insert(lis[i])
  # bs_tree.insert(100)
  bs_tree.delete(58)
  for i in bs_tree:
    print(i, end=" ")
  # print("\n", bs_tree.search(4))

二叉排序树总结：

二叉排序树以链式进行存储，保持了链接结构在插入和删除操作上的优点。

在极端情况下，查询次数为1，但最大操作次数不会超过树的深度。也就是说，二叉排序树的查找性能取决于二叉排序树的形状，也就引申出了后面的平衡二叉树。

给定一个元素集合，可以构造不同的二叉排序树，当它同时是一个完全二叉树的时候，查找的时间复杂度为O(log(n))，近似于二分查找。

当出现最极端的斜树时，其时间复杂度为O(n)，等同于顺序查找，效果最差。

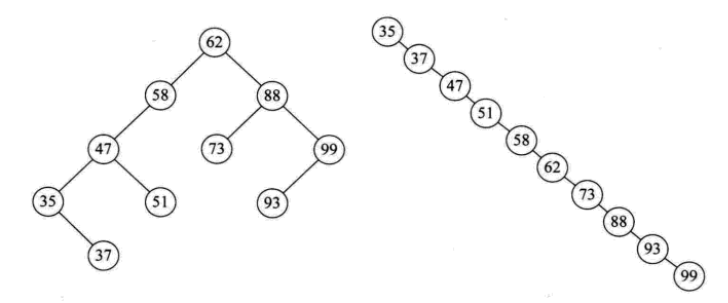
六、 平衡二叉树

平衡二叉树（AVL树，发明者的姓名缩写）：一种高度平衡的排序二叉树，其每一个节点的左子树和右子树的高度差最多等于1。

平衡二叉树首先必须是一棵二叉排序树！

平衡因子（Balance Factor）：将二叉树上节点的左子树深度减去右子树深度的值。

对于平衡二叉树所有包括分支节点和叶节点的平衡因子只可能是-1,0和1，只要有一个节点的因子不在这三个值之内，该二叉树就是不平衡的。

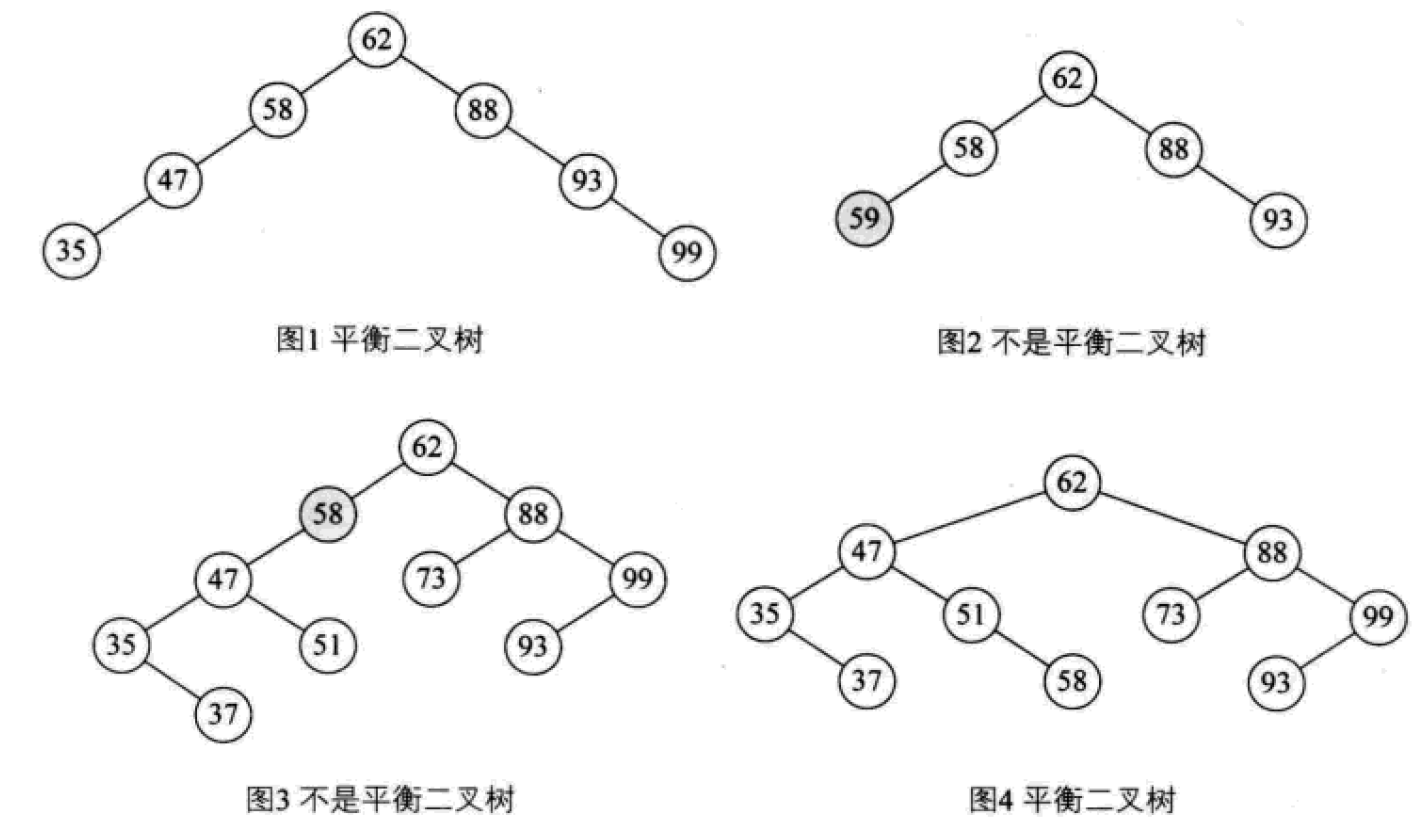
最小不平衡子树：距离插入结点最近的，且平衡因子的绝对值大于1的节点为根的子树。

平衡二叉树的构建思想：每当插入一个新结点时，先检查是否破坏了树的平衡性，若有，找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的连接关系，进行相应的旋转，成为新的平衡子树。

下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树

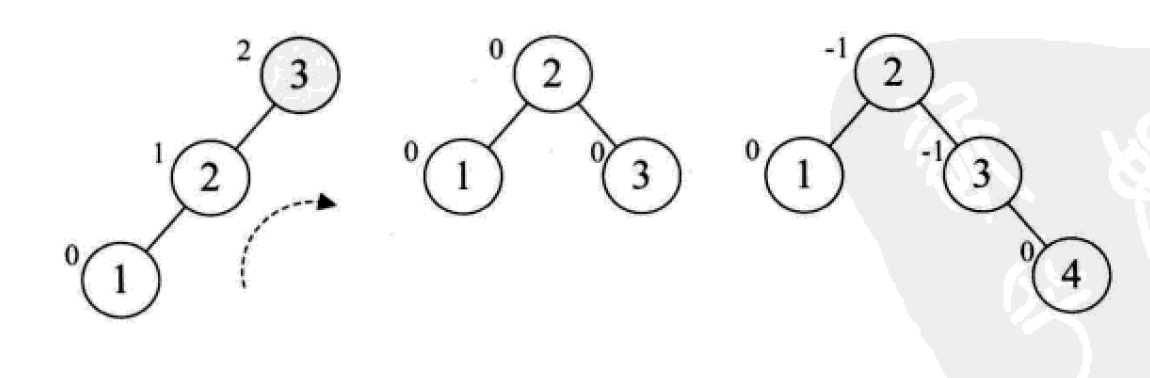
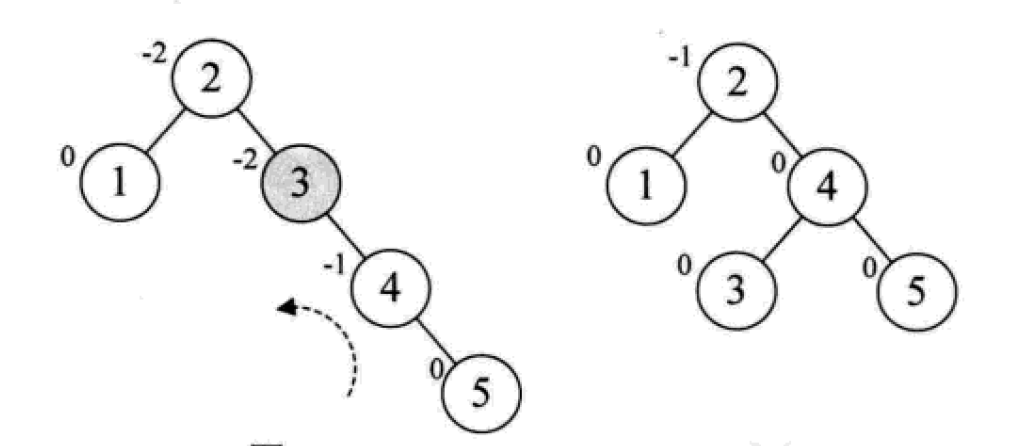
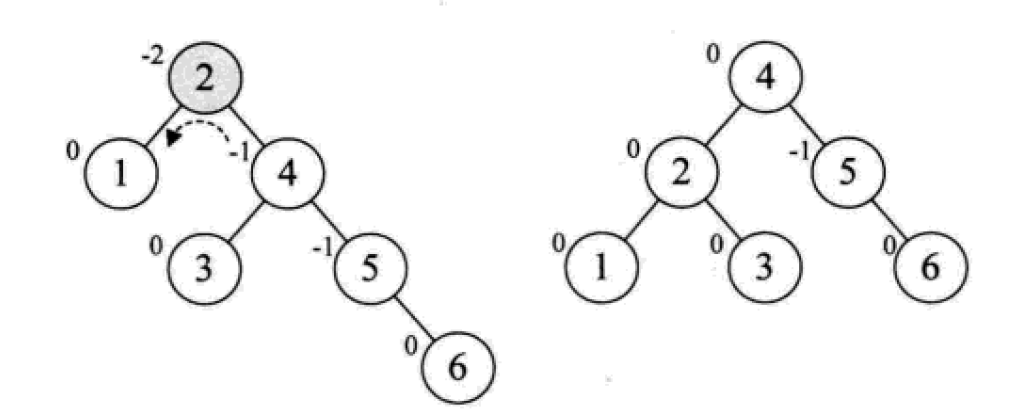
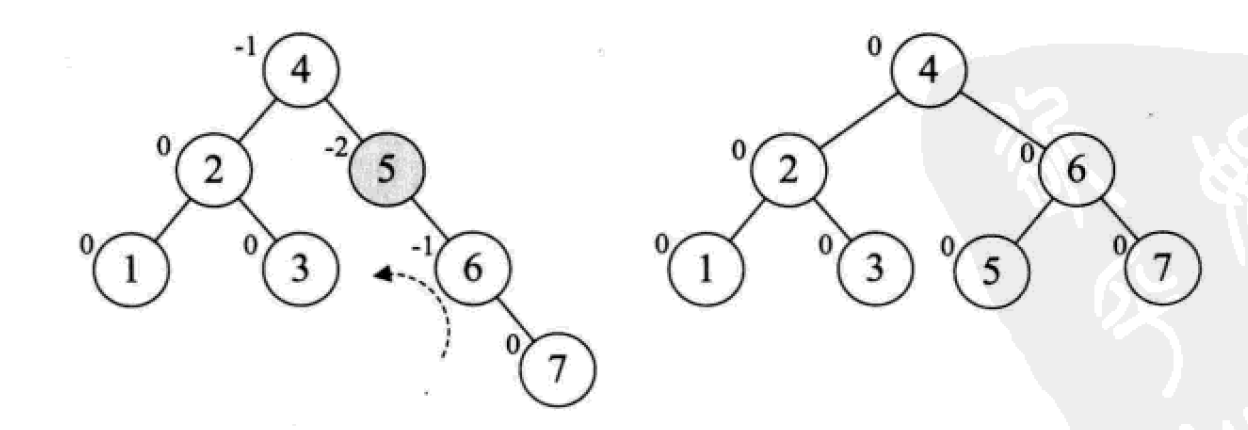
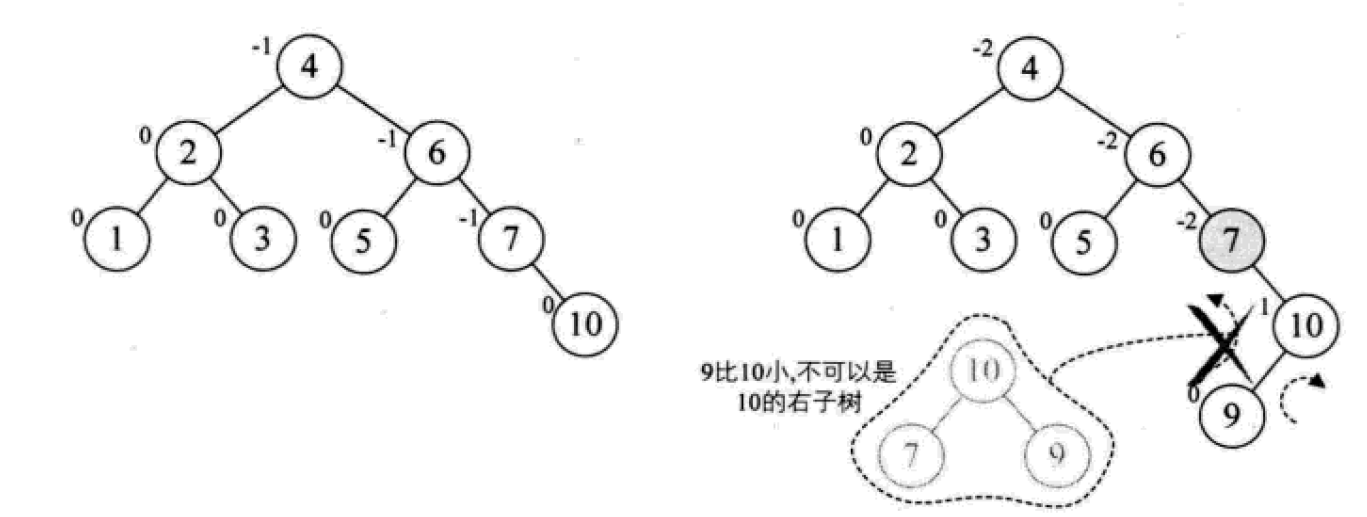
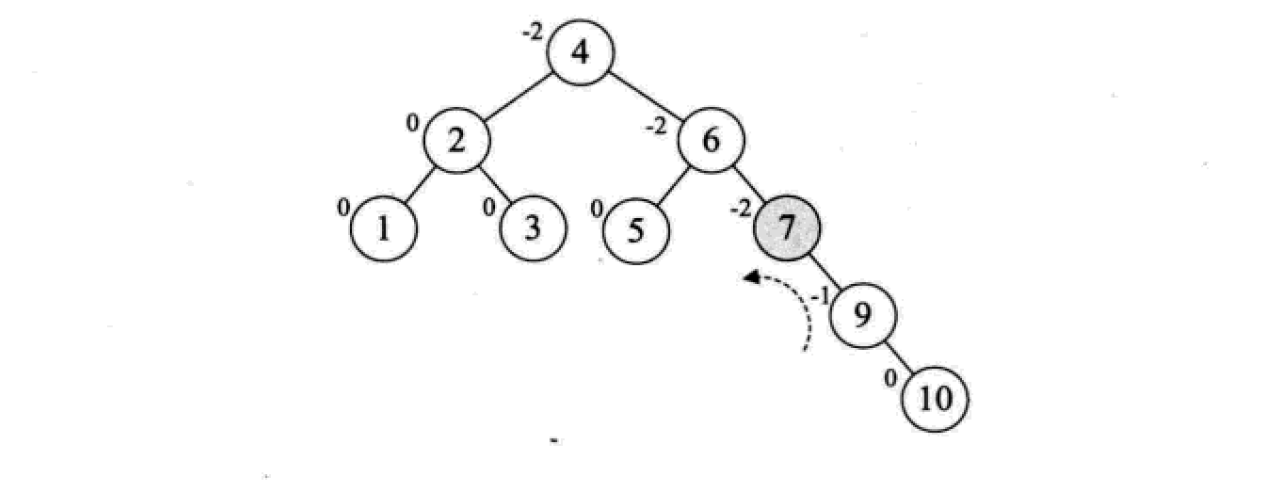
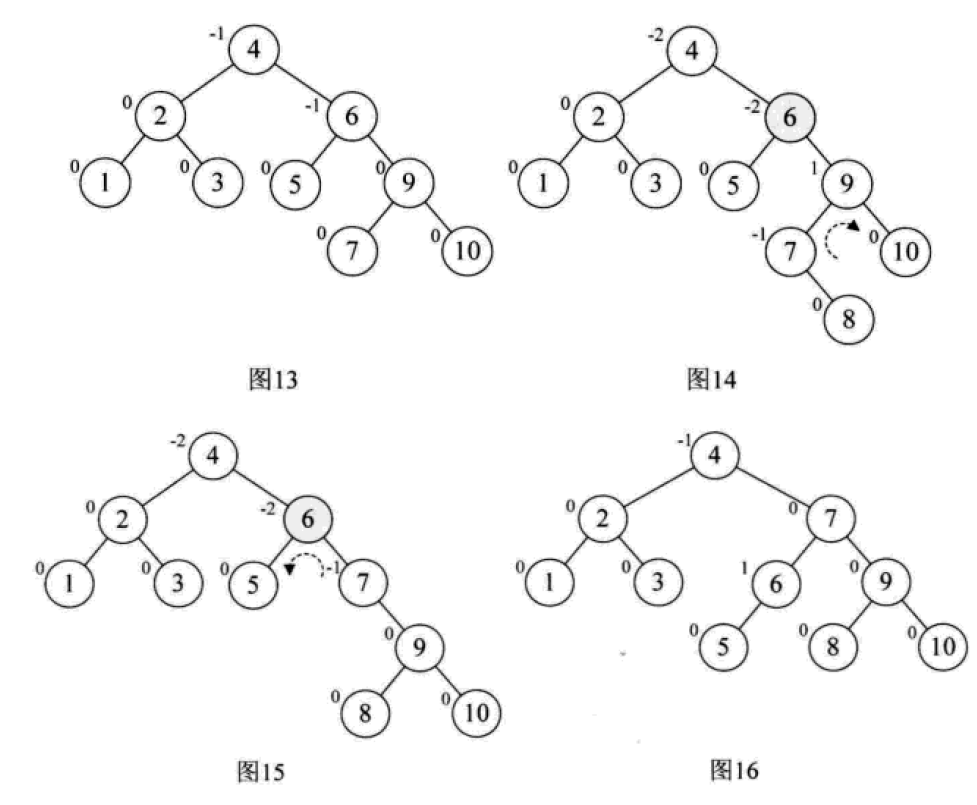
7. 다중 방향 탐색 트리(B-tree)

Muitl-way 탐색 트리(muitl-way 탐색 트리): 각 노드는 2개 이상이 있을 수 있으며, 각 노드는 여러 요소를 저장할 수 있습니다.
다중 방향 검색 트리의 경우 핵심은 각 노드가 저장할 수 있는 요소 수와 해당 하위 항목 수입니다. 일반적으로 사용되는 형식은 2-3 트리, 2-3-4 트리, B 트리입니다. 및 B+ 트리.

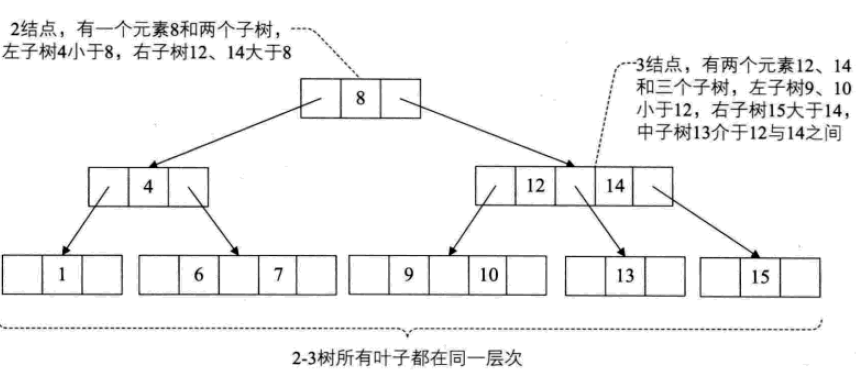
2-3 트리

2-3 트리: 각 노드에는 자식이 2개, 3개 또는 자식이 없습니다.

2노드에는 요소 1개와 하위 2개가 포함됩니다(또는 하위가 없으면 하위 하나만 가질 수 없음). 이진 정렬 트리와 유사하게 왼쪽 하위 트리에 포함된 요소는 모두 해당 요소보다 작고 오른쪽 하위 트리에 포함된 요소는 해당 요소보다 큽니다.

3노드에는 요소 2개와 하위 3개가 포함됩니다(또는 하위가 하나 또는 두 개가 아닌 경우도 있음).

2-3 나무의 모든 잎은 같은 높이에 있어야 합니다.

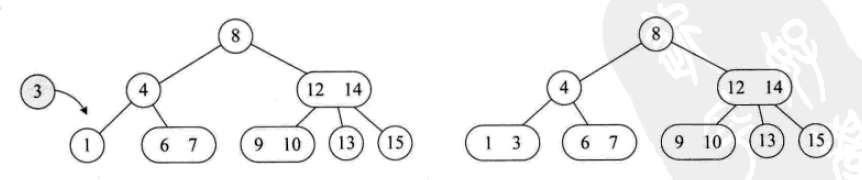
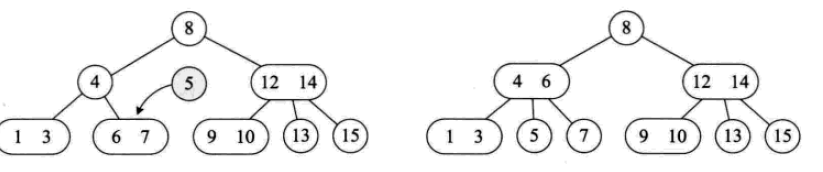
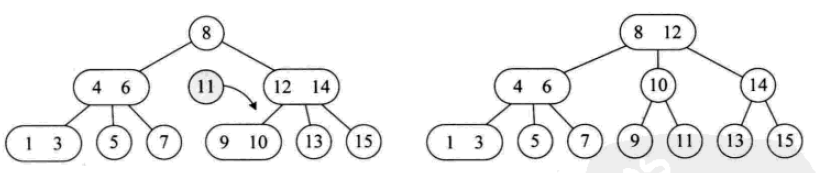
삽입 작업은 다음과 같습니다.

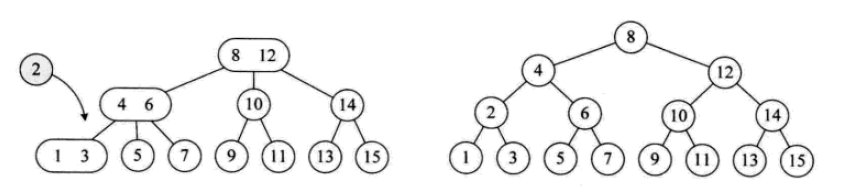
삭제 작업은 다음과 같습니다.

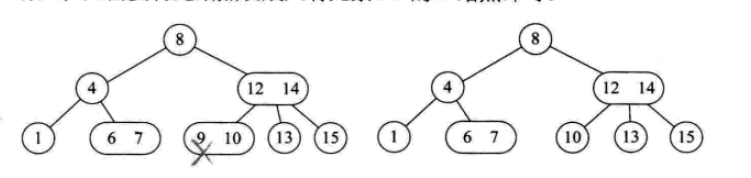
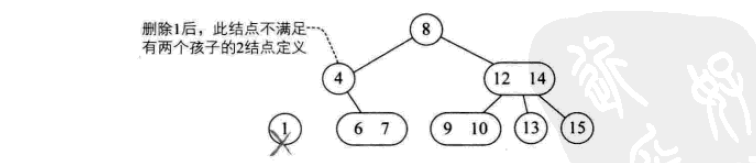
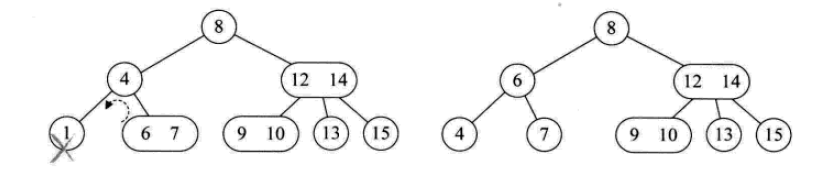
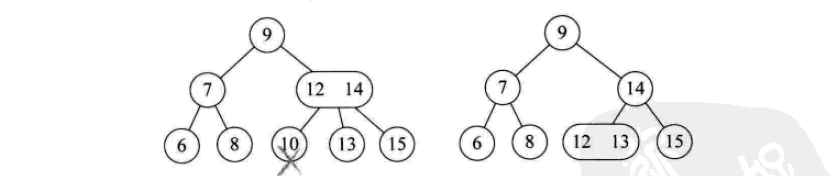
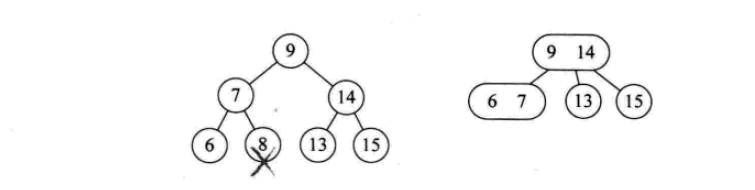
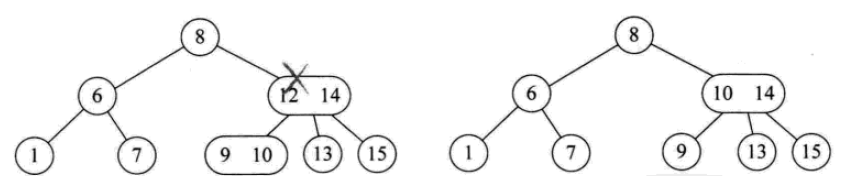
2- 3-4 트리

는 실제로 2-3 트리의 확장으로 4노드 사용을 포함합니다. 4노드에는 소형, 중형, 대형의 세 가지 요소와 4개의 하위 요소(또는 하위 요소 없음)가 포함됩니다.

삽입 작업:

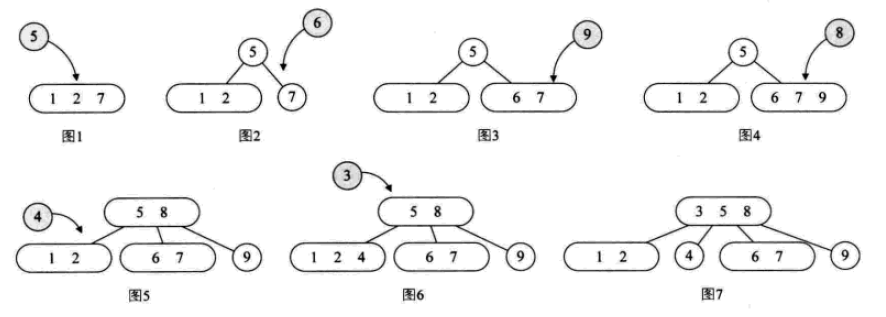
삭제 작업:

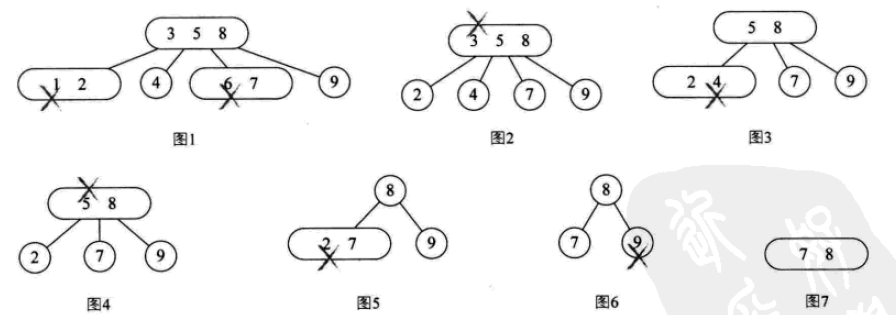
B 트리

B-tree는 균형 잡힌 다방향 탐색 트리입니다. 노드의 최대 자식 수를 B-트리의 순서라고 합니다. 2-3 트리는 3차 B-트리이고, 2-3-4는 4차 B-트리입니다.

B-tree의 데이터 구조는 주로 메모리와 외부 메모리 간의 데이터 상호작용에 사용됩니다.

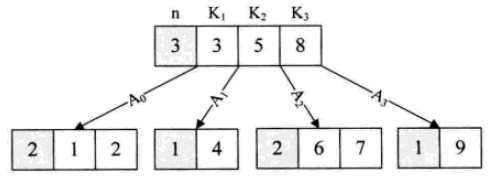
B+ 트리

모든 요소의 순회를 해결하기 위해 of B tree 등. 기본적인 문제는 원래의 구조에 새로운 요소 구성 방법을 추가하면 B+ 트리가 형성된다는 점이다.

B+ 트리는 파일 시스템의 요구에 따라 나타나는 변형 트리입니다. 엄밀히 말하면 더 이상 가장 기본적인 트리는 아닙니다.

B+ 트리에서 가지 노드에 나타나는 요소는 해당 가지 노드 위치에 순서대로 후속 항목(리프 노드)으로 다시 나열됩니다. 또한 각 리프 노드는 다음 리프 노드에 대한 포인터를 저장합니다.

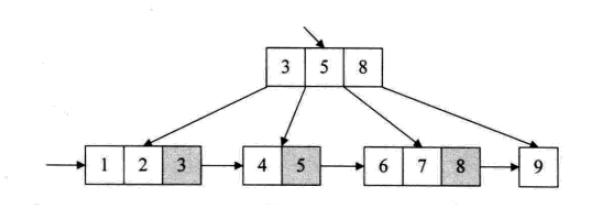
모든 리프 노드에는 모든 키워드 및 관련 포인터에 대한 정보가 포함됩니다. 리프 노드 자체는 키워드의 크기에 따라 오름차순으로 연결됩니다.

B+ 트리의 구조는 특히 범위를 사용한 검색에 적합합니다. 예를 들어, 20세에서 30세 사이의 사람들을 찾으십시오.

8. 해시 테이블(hash table)

해시 테이블: 모든 요소 사이에는 관계가 없습니다. 요소의 저장 위치는 요소의 키워드를 이용한 함수를 통해 직접 계산됩니다. 이러한 일대일 관계 함수를 해시 함수 또는 해시 함수라고 합니다.

해시 기술은 해시 테이블 또는 해시 테이블(Hash Table)이라고 불리는 연속적인 저장 공간에 기록을 저장하는 데 사용됩니다. 키워드에 해당하는 저장 위치를 ​​해시 주소라고 합니다.

해시 테이블은 검색 중심의 저장 구조입니다. 가장 적합한 문제는 주어진 값과 동일한 레코드를 찾는 것입니다. 그러나 "남성" 성별을 모두 찾는 등 특정 키워드가 여러 레코드에 해당할 수 있는 상황에는 적합하지 않습니다. 또한 20~30세의 사람을 검색하는 등 범위 검색에는 적합하지 않습니다. 정렬, 최대, 최소 등도 부적절합니다.

그래서 해시 테이블은 일반적으로 키워드가 반복되지 않는 데이터 구조에 사용됩니다. 예를 들어 Python의 사전 데이터 유형입니다.

단순하고 균일하며 저장 활용도가 높은 해시 함수를 설계하는 것은 해싱 기술에서 가장 중요한 문제입니다.

그러나 일반적인 해시 함수는 충돌 문제에 직면합니다.

충돌: 서로 다른 두 키워드를 해시 함수로 계산한 결과가 동일합니다. 충돌.

8.1 해시 함수 구성 방법

좋은 해시 함수: 간단한 계산, 균일한 해시 주소 분포

1. 직접 주소 지정 방법

예를 들어 키의 선형 함수를 해시 함수로 사용합니다.

f(key) = a*key + b (a, b는 상수)

2.数字分析法

抽取关键字里的数字，根据数字的特点进行地址分配

3.平方取中法

将关键字的数字求平方，再截取部分

4.折叠法

将关键字的数字分割后分别计算，再合并计算，一种玩弄数字的手段。

5.除留余数法

最为常见的方法之一。

对于表长为m的数据集合，散列公式为：

f(key) = key mod p (p<=m)

mod：取模（求余数）

该方法最关键的是p的选择，而且数据量较大的时候，冲突是必然的。一般会选择接近m的质数。

6.随机数法

选择一个随机数，取关键字的随机函数值为它的散列地址。

f(key) = random(key)

总结，实际情况下根据不同的数据特性采用不同的散列方法，考虑下面一些主要问题：

计算散列地址所需的时间

关键字的长度

散列表的大小

关键字的分布情况

记录查找的频率

8.2 处理散列冲突

1、开放定址法

就是一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

公式是：

这种简单的冲突解决办法被称为线性探测，无非就是自家的坑被占了，就逐个拜访后面的坑，有空的就进，也不管这个坑是不是后面有人预定了的。

线性探测带来的最大问题就是冲突的堆积，你把别人预定的坑占了，别人也就要像你一样去找坑。

改进的办法有二次方探测法和随机数探测法。

2、再散列函数法

发生冲突时就换一个散列函数计算，总会有一个可以把冲突解决掉，它能够使得关键字不产生聚集，但相应地增加了计算的时间。

3、链接地址法
碰到冲突时，不更换地址，而是将所有关键字为同义词的记录存储在一个链表里，在散列表中只存储同义词子表的头指针，如下图：

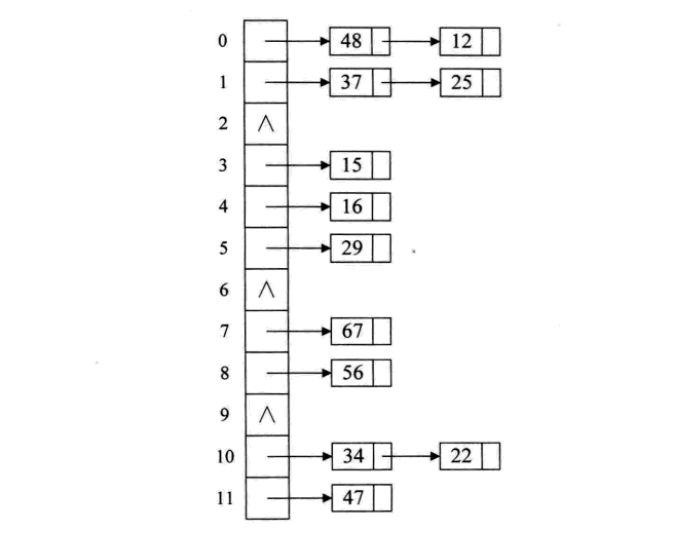
这样的好处是，不怕冲突多；缺点是降低了散列结构的随机存储性能。本质是用单链表结构辅助散列结构的不足。

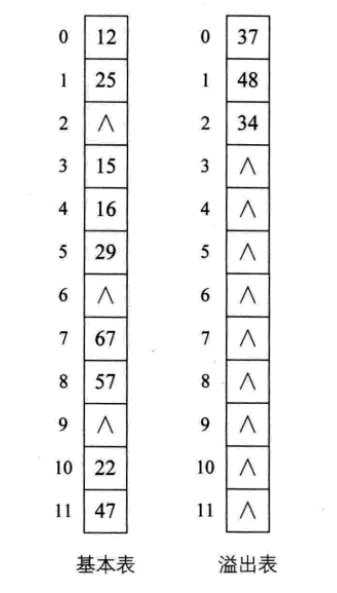
4、公共溢出区法

其实就是为所有的冲突，额外开辟一块存储空间。如果相对基本表而言，冲突的数据很少的时候，使用这种方法比较合适。

8.3 散列表查找实现

下面是一段简单的实现代码：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 忽略了对数据类型，元素溢出等问题的判断。
 
 
class HashTable:
  def __init__(self, size):
    self.elem = [None for i in range(size)] # 使用list数据结构作为哈希表元素保存方法
    self.count = size # 最大表长
 
  def hash(self, key):
    return key % self.count # 散列函数采用除留余数法
 
  def insert_hash(self, key):
    """插入关键字到哈希表内"""
    address = self.hash(key) # 求散列地址
    while self.elem[address]: # 当前位置已经有数据了，发生冲突。
      address = (address+1) % self.count # 线性探测下一地址是否可用
    self.elem[address] = key # 没有冲突则直接保存。
 
  def search_hash(self, key):
    """查找关键字，返回布尔值"""
    star = address = self.hash(key)
    while self.elem[address] != key:
      address = (address + 1) % self.count
      if not self.elem[address] or address == star: # 说明没找到或者循环到了开始的位置
        return False
    return True
 
 
if __name__ == '__main__':
  list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34]
  hash_table = HashTable(12)
  for i in list_a:
    hash_table.insert_hash(i)
 
  for i in hash_table.elem:
    if i:
      print((i, hash_table.elem.index(i)), end=" ")
  print("\n")
 
  print(hash_table.search_hash(15))
  print(hash_table.search_hash(33))

   

8.4 散列表查找性能分析

如果没发生冲突，则其查找时间复杂度为O(1)，属于最极端的好了。

但是，现实中冲突可不可避免的，下面三个方面对查找性能影响较大：

散列函数是否均匀

处理冲突的办法

散列表的装填因子（表内数据装满的程度）

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持PHP中文网。

更多일반적으로 사용되는 검색 데이터 구조 및 알고리즘에 대한 자세한 설명(Python 구현)相关文章请关注PHP中文网！