동적 프로그래밍 프로그래밍은 최적화 문제를 해결하는 방법이자 방법입니다. 최종 문제의 최적 솔루션은 이전 하위 문제의 최적 솔루션에서 파생될 수 있습니다.
동적 프로그래밍 알고리즘의 경우 아직 완전히 배우지 않았습니다. 학습 경험을 간단히 요약하면 다음과 같습니다.
동적 프로그래밍의 아이디어는 재귀와 분할 및 정복. 그러나 동적 프로그래밍 솔루션에서는 분할 및 정복과 달리 솔루션 프로세스의 각 분기의 최적 솔루션이 상태를 통해 기록되므로 여러 분기의 반복 계산이 절약됩니다.
동적 프로그래밍에서 가장 중요하고 어려운 두 단계는 하위 문제를 설명하는 상태와 상태 간의 파생 관계를 찾는 것입니다.
동적 프로그래밍을 사용할 가능성이 더 높은 문제: 최대값과 최소값 찾기, 실현 가능한 솔루션이 있는지 여부 및 실현 가능한 솔루션의 수.
가장 흔한 질문인 피보나치 수열에서 특정 위치의 값을 먼저 찾아볼까요(모르는 학생들은 바이두에서 검색해 보세요)?
분할 정복 방법을 적용하여 코드 해결

분할 정복 과정에서는 그림 3과 같은 작업이 많이 반복됩니다. 아래 2번은 2번 반복되었습니다. 인덱스 값이 클수록 더 많이 반복됩니다.
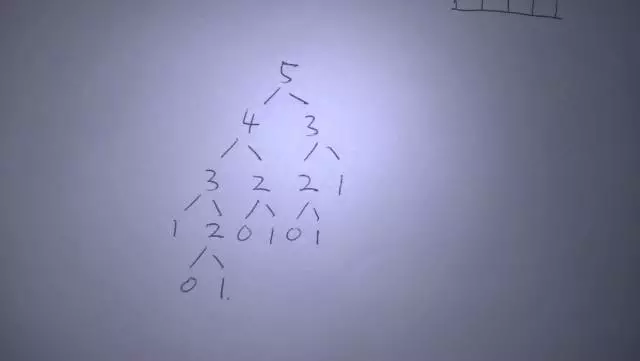
자, 동적 프로그래밍이 어떻게 최적화될 수 있는지 살펴보겠습니다.
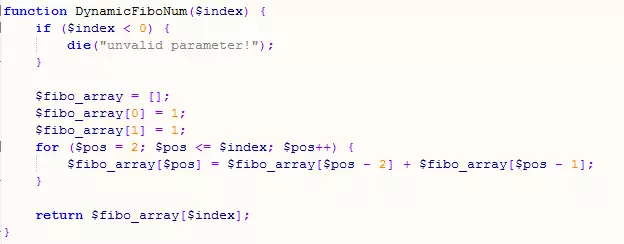
각 피보나치 위치의 값을 기록하기 위해 배열을 정의합니다. 이는 각 위치의 값을 정의하는 것과 같습니다. 이전 두 개의 합은 상태 전이 방정식과 동일합니다.
여기서 배열을 통해 상태를 기록한다는 것은 공간을 시간으로 교환한다는 개념입니다. 사실 우리가 일상적인 개발에서 사용하는 캐시 디자인과 매우 유사합니다.
요약 동적 프로그래밍 솔루션은 4단계로 나눌 수 있습니다.
1. 해결해야 할 하위 문제, 즉 상태 정의를 결정합니다.
2. 상태 전이 방정식을 나열합니다.
3. 주어진 조건에 따라 알려진 상태 값을 초기화합니다.
4. 최종 문제 해결 방법을 해결하세요.
계단 오르기라는 더 흥미로운 문제를 해결해 보겠습니다.

위는 PHP 알고리즘 학습의 동적 프로그래밍 내용입니다. 관련 내용에 더 주목해 주세요. 내용 PHP 중국어 웹사이트(www.php.cn)!