WeChat 빨간 봉투의 구현 원칙에 대한 추측

다음 내용은 QCon에서 고가용성 아키텍처 그룹의 채팅 기록 배경에서 가져온 것입니다. 친구가 WeChat 빨간 봉투의 아키텍처에 대해 상담했으며, 다음 토론 내용은 공식 또는 토론에서 도출되었습니다. 이 기간 동안 많은 A급 친구가 현재 네트워크에서 알고리즘을 테스트하기 위해 빨간 봉투를 보냈습니다.

빨간 봉투를 집는 과정

누군가가 N명의 그룹에게 빨간 봉투를 보내면 그 배경에는 무슨 일이 일어나는가?

1. 빨간 봉투 보내기를 위한 백그라운드 작업:

빨간 봉투 레코드를 데이터베이스에 추가하고 CKV에 저장하고 만료 시간을 설정합니다. >캐시(아마도 Tencent의 내부 kv 데이터베이스, 메모리 기반으로 구현되었으며 커널 모듈 형태로 서비스를 제공하기 위한 커널 상태 네트워크 처리 모듈이 있음)) 잡는 사람 수를 저장하는 레코드를 추가합니다. 빨간 봉투 N

2. 빨간 봉투 잡기를 위한 백스테이지 작업:

빨간 봉투 잡기 Cache 레이어에서 잡기 작업이 완료됩니다. 0이 될 때까지 원자 빼기 연산을 통해 감소됩니다. 이는 결국 백그라운드 해제 작업의 실제 양이 크지 않다는 것을 의미합니다. 작업 분리를 통해 잘못된 요청은 캐시 계층 외부에서 직접 차단됩니다. 여기서의 원자 빼기 연산은 진정한 의미의 원자 빼기 연산은 아니지만, 캐시 레이어에서 제공하는 CAS는 버전 번호를 비교하여 계속 시도합니다. 충돌하는 사용자는 해제되고 다음 분해 작업을 진행할 수 있습니다. 이는 일부 사용자가 해체 작업을 수행하는 이유이기도 합니다. ​ 개발이 완료된 상황.

빨간 봉투 개봉은 데이터베이스에서 완료되며, 데이터베이스의 트랜잭션 작업을 통해 수신된 수와 금액이 누적되고 청구가 삽입됩니다. ​ 흐르는 물과 녹음은 비동기식 작업이므로 춘제 기간 동안 빨간 봉투를 받은 후 저울에서 볼 수 없는 이유도 설명됩니다. 금액은 분할 시 실시간으로 계산되며, 금액은 총액의 1포인트에서 2배 사이의 임의의 숫자입니다. M 위안 상당의 빨간 봉투, 가장 큰 빨간 봉투는 M * 2 /N(M을 초과하지 않음), 빨간 봉투를 열면 남은 금액과 개수가 업데이트됩니다. 텐페이는 초당 20만 건의 거래를 준비하고 있지만 실제 거래량은 초당 8만건에 불과하다.

FAQ

잡을 때 원자가 줄어들기 때문에, 잡은 후에도 분해되지 않는 상황이 있어야 하지 않을까요?

여기서의 원자 빼기는 진정한 의미의 원자 연산이 아니라 버전 번호를 비교하여 끊임없이 시도되는 캐시 계층에서 제공하는 CAS입니다.

캐시와 DB가 다운된 경우 어떻게 해야 하나요?

프라이머리와 백업 + 조정

없어진 빨간 봉투도 있는데 잔액은 그대로 남아있나요?

아니요, 프로그램은 마지막에 모든 작업을 수행하고 비동기 조정을 보장합니다.

잡기와 철거를 분리하는 이유는 무엇인가요?

일반적인 아이디어는 다층 필터를 설정하고 층별로 필터링한 다음 층별로 흐름과 압력을 줄이는 것입니다. 이 디자인은 원래 잡기 작업이 비즈니스 계층이고 분할 작업이 회계 작업이므로 한 작업이 너무 무겁고 중단 비율이 높기 때문입니다. ​ 인터페이스 수준에서 첫 번째 인터페이스는 순수한 캐시 작업이며 강력한 압축 기능을 갖추고 있습니다. 간단한 쿼리 캐시는 대부분의 사용자를 차단하고 첫 번째 필터링을 수행하므로 대부분의 사람들에게 콘텐츠가 매진되었다는 메시지가 표시됩니다.

빨간 봉투를 잡은 후 보내거나 현금을 인출하는 전략이 있나요?

거액 우선입금 전략

각 빨간 봉투의 확률이 동일한지 여부를 증명할 데이터가 있나요?

절대적으로 동일하지는 않습니다. 단순한 두뇌 패팅 알고리즘일 뿐입니다.

머리 쓰다듬기 알고리즘 중에 가장 좋은 게 두 개 있을까요?

같은 금액이겠지만 행운의 사람은 딱 하나, 먼저 잡는 사람이 최고입니다.

빨간 봉투를 준 사람의 돈은 동결되나요?

동결이 아닌 실시간으로 직접 차감됩니다.

실시간 금액계산을 이용하는 이유는 무엇인가요?

실시간 효율성은 높지만 예산 효율성은 낮습니다. 예산에는 추가 저장용량도 포함됩니다. 빨간 봉투는 하나의 기록만을 차지하고 며칠 동안만 유효하기 때문에 많은 공간을 차지하지 않습니다. 압력이 높아도 수평팽창기는 그렇습니다.

테스트 2: Zhihu 사용자 "Ma Jingchen"의 실험:

여기 100개의 샘플 설문조사 샘플 데이터가 있으며 여러분만의 추측을 제시해 보세요.

1. 지갑머니는 검열된 일반 난수 분포를 만족합니다. 대략적으로 말하면, 검열된 정규분포에서 난수를 취하고, 합산된 수를 전체 값으로 나눠서 보정 인자를 얻은 다음, 모든 난수에 보정 인자를 곱하여 레드 엔벨로프 값을 얻습니다.

이 분포는 평균보다 낮지만 평균과 크게 다르지 않은 빨간 봉투가 더 많고, 평균보다 훨씬 큰 빨간 봉투가 더 많다는 것을 의미합니다.

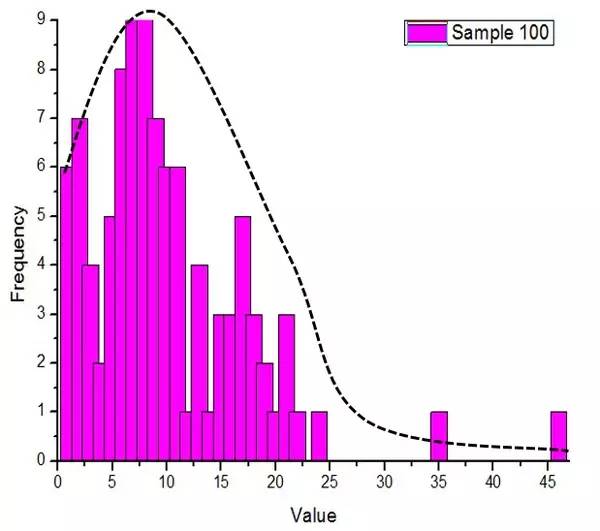그림 1. 지갑 가치와 빈도 분포 히스토그램 및 정규 피팅

그러나 분포 히스토그램을 보면 정규 분포를 따른다고 추론할 수는 없습니다. distribution 이지만 프로그램의 단순성과 난수의 합리성을 고려하면 이것이 가장 합리적인 추측입니다.

2. 일반적으로 최신 지갑이 더 가치가 높습니다

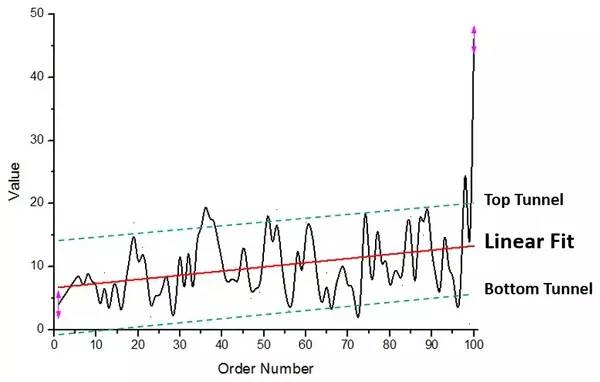그림 2. 지갑 일련번호와 해당 가치의 관계 곡선

그림 2의 선형 피팅 빨간색 선을 보면 지갑 가치의 전반적인 변화 추세가 서서히 증가하고 있음을 알 수 있으며, 그 변화 범위는 대략 녹색 점선의 상한과 하한으로 구분되는 "채널"입니다. . (곡선은 규칙 1의 합리성을 측면에서 반영하고 난수가 균일하게 분포되지 않음을 보여주는 이러한 규칙적인 "채널"로 둘러싸여 있을 수 있습니다.)

다른 평균에서 이 패턴도 볼 수 있습니다. 그림에서.

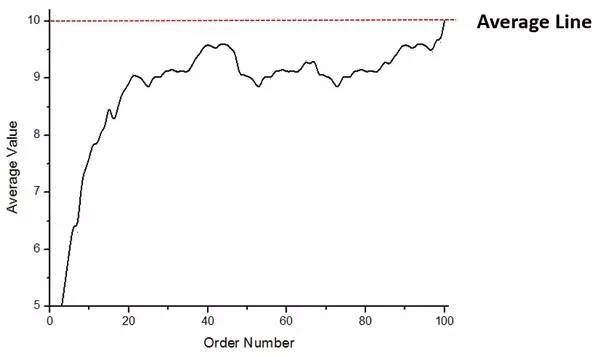
그림 3. 순번에 따른 평균 숫자의 변화 곡선

샘플에서는 1000짜리 지갑 100개로 나누었으니 평균은 10이다. 그러나 그림 3을 보면 마지막 지갑 이전에는 평균이 10보다 낮아 초반에는 지갑의 가치가 낮았으나 후반에는 지갑의 가치만큼 상승한 것을 알 수 있다. 기간 값이 더 높습니다.

3. 물론 평균 그래프는 또 다른 규칙을 드러낼 수도 있습니다. 즉, 마지막 사람이 더 많은 것을 그릴 만큼 운이 좋은 경우가 많습니다. 마지막 사람이 지갑에 남은 모든 것을 가져가고 이전 모든 사람의 평균이 10 미만이기 때문에 적어도 마지막 사람이 평균보다 높을 것이라는 것이 보장됩니다. 이 샘플에서 지갑 번호 98은 35를 그렸고, 마지막 지갑은 46을 그렸습니다.

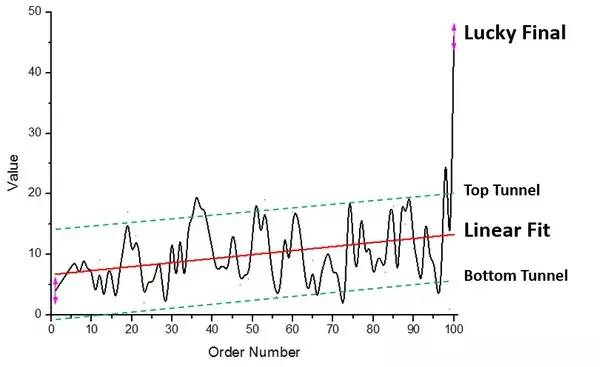
요약하자면, 샘플 추측으로:

1. 대부분의 경우 뽑힌 돈은 남들만큼 적지만, 한번 해보면 많을수록 훨씬 쉬워집니다.

2. 뒷면에 지갑을 더 많이 그릴수록 돈벌기가 더 쉬워집니다.

3. 마지막 사람이 운이 좋은 경우가 많다.