--------- ------ ------------------ ------ ------------------ ------ ------------------ ------ --
TreeMap의 구현은 레드-블랙 트리 알고리즘의 구현이므로 TreeMap을 이해하려면 특정 지식이 있어야 합니다. 실제로 이 블로그 게시물의 이름은 다음과 같습니다. 레드-블랙 트리 알고리즘을 기반으로 하는 TreeMap의 구현을 분석하지만 Java 개선 블로그 게시물 시리즈와 일관성을 유지하려면 다음을 수행하는 것이 좋습니다. 그것을 트리맵이라고 부르세요. 본 블로그 포스팅을 통해 다음과 같은 지식 포인트를 얻을 수 있습니다.
1. 레드-블랙 트리의 기본 개념.
2. 레드-블랙 트리에 노드를 추가하고 삭제하는 구현 과정.
3. 빨간색과 검은색 나무의 왼쪽 회전과 오른쪽 회전의 복잡한 과정.
4. Java의 TreeMap은 어떻게 put 및 deleteEntry를 사용하여 레드-블랙 트리에 노드를 추가하고 삭제합니다.
이번 포스팅을 통해 TreeMap에 대한 이해가 더 깊어지셨을 거라 생각합니다. 자, 레드-블랙 트리에 대한 지식을 간략하게 대중화해 보겠습니다.
레드-블랙 트리 트리는 레드-블랙 이진 트리라고도 알려져 있으며, 우선 이진 트리이며 이진 트리의 모든 특성을 구현합니다. 동시에 레드-블랙 트리는 자체 균형 정렬 이진 트리입니다.
우리는 기본 이진 트리가 기본 속성을 충족해야 한다는 것을 알고 있습니다. 즉, 트리에 있는 모든 노드의 값은 왼쪽 자식 노드보다 크고 오른쪽 자식 노드보다 작습니다. 노드. 이 기본 속성에 따르면 트리의 검색 효율성이 크게 향상됩니다. 우리는 이진 트리를 생성하는 과정이 불균형하기가 매우 쉽다는 것을 알고 있습니다. 최악의 시나리오는 단방향(오른쪽/왼쪽 하위 트리만)입니다. 이는 필연적으로 이진 트리(O()의 검색 효율성을 크게 감소시킵니다. n)) 따라서 이진 트리의 균형을 유지하기 위해 전문가들은 AVL, SBT, 스프레드 트리, TREAP, 레드-블랙 트리 등과 같은 다양한 구현 알고리즘을 제안했습니다.
균형 이진 트리는 다음과 같은 특징을 가져야 합니다: 빈 트리이거나 왼쪽 및 오른쪽 하위 트리 사이의 높이 차이의 절대값이 1을 초과하지 않으며 왼쪽 및 오른쪽 하위 트리 모두 오른쪽 하위 트리는 균형 잡힌 이진 트리입니다. 즉, 이진 트리의 모든 하위 노드에 대해 왼쪽 및 오른쪽 하위 트리의 높이가 비슷합니다.
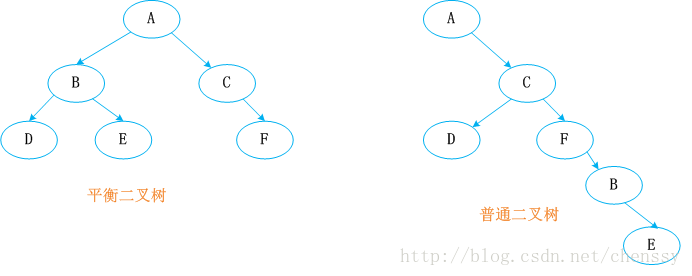
이름에서 알 수 있듯이 레드-블랙 트리는 레드 또는 블랙 노드의 균형을 유지하는 균형 잡힌 이진 트리입니다. 색상 제약을 통한 이진 트리. 효과적인 레드-블랙 이진 트리를 위해서는 다음 규칙을 추가해야 합니다:
2. 루트 노드는 검정색
3. 각 리프 노드(NIL 노드, 빈 노드)는 검정색입니다.
4. 노드가 빨간색이면 두 개의 하위 노드가 있습니다. 노드는 모두 검은색입니다. 즉, 인접한 두 개의 빨간색 노드가 경로에 나타날 수 없습니다.
5. 모든 노드에서 각 리프까지의 모든 경로에는 다음이 포함됩니다. 동일한 수의 블랙 노드.
이러한 제약 조건은 레드-블랙 트리의 주요 속성을 적용합니다. 루트에서 리프까지 가능한 가장 긴 경로는 최단 경로에 지나지 않습니다. 가능한 경로는 두 배 더 길어집니다. 결과는 대략적으로 균형이 잡힌 트리입니다. 값 삽입, 삭제, 조회 등의 작업에 대한 최악의 시간은 트리의 높이에 비례해야 하므로, 이러한 이론적 높이 상한은 최악의 경우에도 레드-블랙 트리가 효율적일 수 있도록 해준다. 일반적인 이진 검색 트리와는 다릅니다. 따라서 레드-블랙 트리는 복잡하고 효율적이며, 검색 효율은 O(log n)이다. 아래 그림은 전형적인 레드-블랙 이진 트리를 보여줍니다.

왼쪽 회전, 오른쪽 회전, 색칠의 세 가지 기본 작업이 포함됩니다.
왼손 회전
이 섹션의 참고 자료 :http://www.php .cn/Baidu 백과사전
참고:이후 이 기사에서는 주로 Java의 TreeMap을 설명하지만 레드-블랙 트리에 대한 심층적인 이해와 연구는 없습니다. 이에 대해 더 깊이 있는 연구를 수행하고 싶다면 몇 가지 좋은 블로그 게시물을 제공하겠습니다.
1, 빨간색과 검은색 나무 시리즈 하이라이트
🎜>분석 레드-블랙 트리 데이터 구조 3.
빨간색과 검은색 나무
2. TreeMap 데이터 구조
TreeMap은 다음과 같이 정의됩니다.
public class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.Serializable<p><span style="font-size:14px;"><span style="font-size:14px;"><strong><span style="font-size:14px;"></span></strong> </span></span></p>TreeMap은 AbstractMap을 상속하고 NavigableMap, 복제 가능 및 직렬화 가능 인터페이스를 구현합니다. 그 중 AbstractMap은 TreeMap이 키-값 컬렉션을 지원하는 Map임을 나타내며, NavigableMap(more)은 일련의 탐색 메서드를 지원하고 지정된 검색 대상에 대해 가장 가까운 일치 항목을 반환하는 탐색 메서드가 있음을 의미합니다. <p style="padding: 5px; border: 1px solid rgb(204, 204, 204); background-color: rgb(245, 245, 245);" class="cnblogs_code"></p> <p></p> <p><span style="font-size:14px;"><span style="font-size:14px;"> <strong><span style="font-size:14px;"></span>TreeMap에는 다음과 같은 중요한 속성도 포함되어 있습니다. </strong></span><p style="padding: 5px; border: 1px solid rgb(204, 204, 204); background-color: rgb(245, 245, 245);" class="cnblogs_code"></p> <pre class="brush:php;toolbar:false">//比较器,因为TreeMap是有序的,通过comparator接口我们可以对TreeMap的内部排序进行精密的控制 private final Comparator<? super K> comparator; //TreeMap红-黑节点,为TreeMap的内部类 private transient Entry<K,V> root = null; //容器大小 private transient int size = 0; //TreeMap修改次数 private transient int modCount = 0; //红黑树的节点颜色--红色 private static final boolean RED = false; //红黑树的节点颜色--黑色 private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子 Entry<K,V> left = null; //右孩子 Entry<K,V> right = null; //父亲 Entry<K,V> parent; //颜色 boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
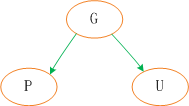
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
새로 삽입된 노드 N에 상위 노드가 없으면 노드로 직접 삽입할 수 있습니다. 색상을 검정색으로 설정합니다. (그림 1의 (1)과 같이)
2. 부모 노드가 검정색임
빨간색, 규칙 4에 따르면 두 개의 검은 리프 노드가 있고 값은 다음과 같습니다. 널. 동시에, 새 노드 N은 빨간색이므로 자식 노드를 통과하는 경로에는 여전히 동일한 수의 검은색 노드가 포함되며 이는 규칙 5도 충족합니다. (그림 1의 (2)와 같이)
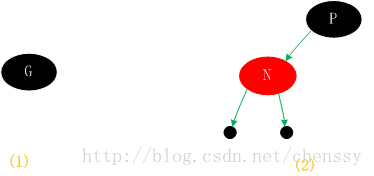
(그림 1)
3. 상위 노드 P와 P의 형제 노드 U가 모두 빨간색인 경우
이런 경우 직접 삽입하면 분명 불균형이 발생합니다. 그것을 처리하는 방법? P 및 U 노드는 검은색으로 변하고 G 노드는 빨간색으로 변합니다. 이때 노드 P와 U를 통과하는 경로는 반드시 G를 통과해야 하므로 이들 경로에 있는 블랙 노드의 개수는 여전히 동일하다. 그러나 위의 처리 후에 G 노드의 상위 노드도 빨간색이 될 수 있습니다. 이때 G 노드를 재귀적으로 새 노드로 처리해야 합니다.

이 경우에는 새로운 노드 N과 P에 대해 왼쪽 회전을 수행합니다. 여기서 생성된 결과는 실제로 완료되지 않았으며 균형이 맞지 않습니다(규칙 4 위반). 이것이 사례 5에서 수행해야 하는 작업입니다.
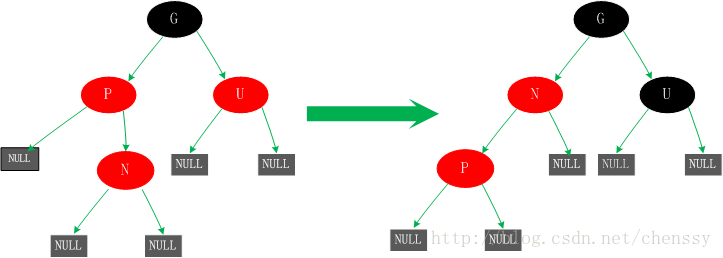
5. 상위 노드 P는 빨간색이고, 삼촌 노드 U는 검정색이거나 누락되어 있으며, 새 노드 N은 상위 노드 P의 왼쪽 자식입니다.
이 상황은 상황 4에 의한 것일 수도 있고 아닐 수도 있습니다. 이 경우, 회전 후 생성된 트리에서는 P 노드를 중심으로 먼저 오른쪽으로 회전합니다. 노드 P는 노드 N과 G의 부모 노드입니다. 하지만 이 트리는 표준화되어 있지 않으며 규칙 4를 위반하므로 P 노드와 G 노드의 색상을 교환하여 사양을 충족시킵니다. 처음에는 모든 경로가 G를 통과해야 하고 블랙 노드의 수가 동일하지만 이제 모든 경로가 P를 통과하고 P가 전체 트리에서 유일한 블랙 노드이므로 조정된 트리도 사양 5를 충족합니다.
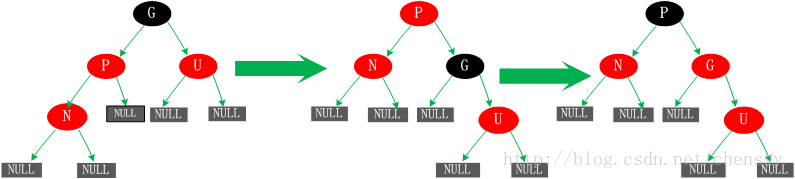
위는 레드-블랙 트리에 새로운 노드를 추가하는 5가지 상황을 보여줍니다. 상황 커버 모든 새로운 가능성을 통해 레드-블랙 트리가 아무리 복잡하더라도 이 다섯 가지 상황에 따라 생성될 수 있습니다. Java의 TreeMap이 레드-블랙 트리를 구현하는 방법을 분석해 보겠습니다.
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。
对于排序二叉树的创建,其添加节点的过程如下:
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
public V put(K key, V value) {
//用t表示二叉树的当前节点
Entry<K,V> t = root;
//t为null表示一个空树,即TreeMap中没有任何元素,直接插入
if (t == null) {
//比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序?
compare(key, key); // type (and possibly null) check
//将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root
root = new Entry<>(key, value, null);
//容器的size = 1,表示TreeMap集合中存在一个元素
size = 1;
//修改次数 + 1
modCount++;
return null;
}
int cmp; //cmp表示key排序的返回结果
Entry<K,V> parent; //父节点
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; //指定的排序算法
//如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合
if (cpr != null) {
do {
parent = t; //parent指向上次循环后的t
//比较新增节点的key和当前节点key的大小
cmp = cpr.compare(key, t.key);
//cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点
if (cmp < 0)
t = t.left;
//cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点
else if (cmp > 0)
t = t.right;
//cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值
else
return t.setValue(value);
} while (t != null);
}
//如果cpr为空,则采用默认的排序算法进行创建TreeMap集合
else {
if (key == null) //key值为空抛出异常
throw new NullPointerException();
/* 下面处理过程和上面一样 */
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//将新增节点当做parent的子节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新增节点的key小于parent的key,则当做左子节点
if (cmp < 0)
parent.left = e;
//如果新增节点的key大于parent的key,则当做右子节点
else
parent.right = e;
/*
* 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置
* 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况
*/
fixAfterInsertion(e);
//TreeMap元素数量 + 1
size++;
//TreeMap容器修改次数 + 1
modCount++;
return null;
}上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
/**
* 新增节点后的修复操作
* x 表示新增节点
*/
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //新增节点的颜色为红色
//循环 直到 x不是根节点,且x的父节点不为红色
while (x != null && x != root && x.parent.color == RED) {
//如果X的父节点(P)是其父节点的父节点(G)的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取X的叔节点(U)
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == rightOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateLeft(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateRight(parentOf(parentOf(x)));
}
}
//如果X的父节点(P)是其父节点的父节点(G)的右节点
else {
//获取X的叔节点(U)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == leftOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateRight(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateLeft(parentOf(parentOf(x)));
}
}
}
//将根节点G强制设置为黑色
root.color = BLACK;
}对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
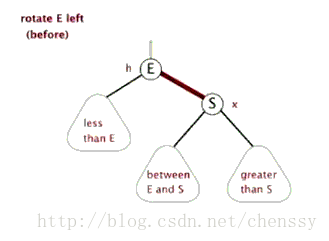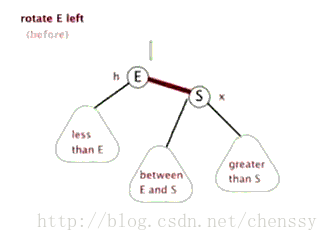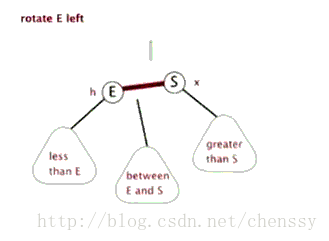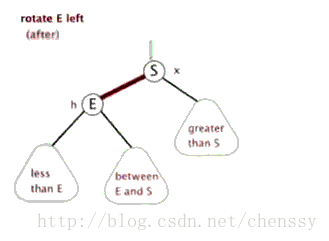
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
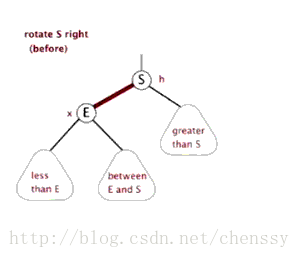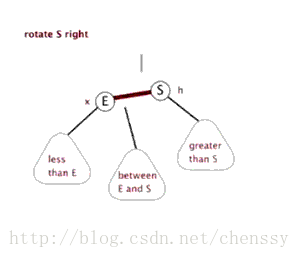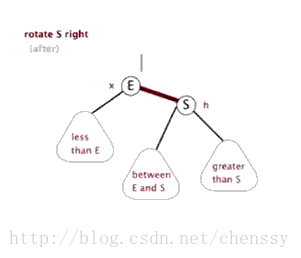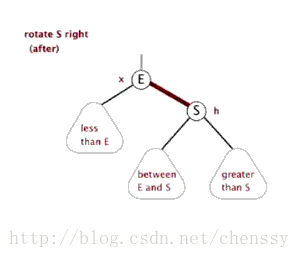
右旋:rotateRight()
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
}所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}左旋、右旋的示意图如下:

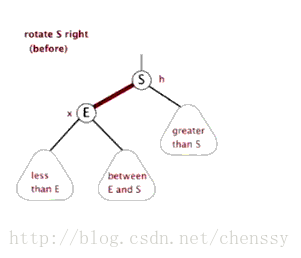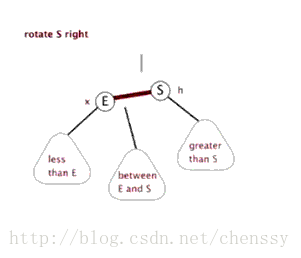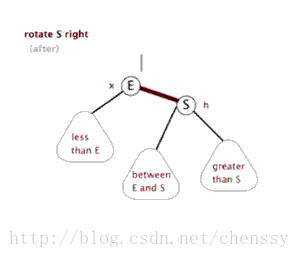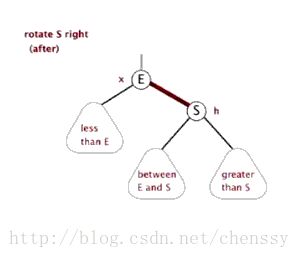
(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。
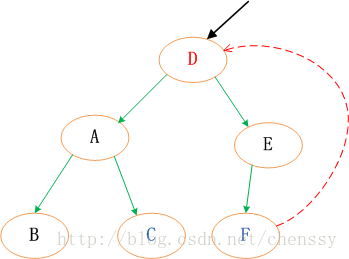
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1. 각 노드는 빨간색 또는 검정색만 가능합니다.
2. 루트 노드는 검정색입니다
3. 각 리프 노드(NIL 노드, 빈 노드)는 검정색입니다.
4. 노드가 빨간색이면 두 개의 하위 노드가 있습니다. 노드는 모두 검은색입니다. 즉, 인접한 두 개의 빨간색 노드가 경로에 나타날 수 없습니다.
5. 모든 노드에서 각 리프까지의 모든 경로에는 다음이 포함됩니다. 같은 수의 블랙 노드.
O(∩ _∩)오~)
맞습니다. 노드를 삭제하는 것이 더 복잡하므로 여기서 규칙에 동의합시다.
1. 다음 설명하는 삭제 노드는 삭제하려는 실제 노드의 후속 노드(N)여야 하며, 위에서 언급한 C와 같은 것입니다.
2. 아래에서 언급하는 노드 삭제용 트리는 다음과 같은 구조를 가지며, 그 구조가 선택된다. node는 삭제할 노드 오른쪽 트리의 가장 왼쪽 자식 노드입니다. 여기서는 실제 삭제된 노드는 N, 부모 노드는 P, 형제 노드는 W, 형제 노드의 두 자식 노드는 X1과 X2라고 규정합니다. 아래 (2.1)과 같습니다.
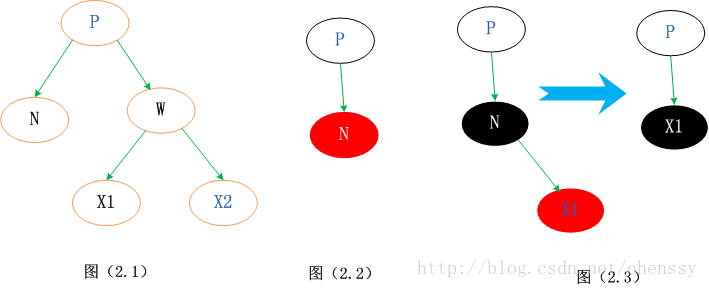
이제 위에서 언급한 세 가지 상황을 분석하고 처리해 보겠습니다.
사례 1, 하위 노드 없음(빨간색 노드)
이 경우 트리 구조에 영향을 주지 않고 노드를 직접 삭제할 수 있습니다. 노드는 리프 노드이므로 자식 노드를 가질 수 없다 ----- 자식 노드가 블랙이면 블랙 노드 수의 원칙(5조)에 위배되고, 레드이면 " 색상' 원칙(제4조). 위의 그림(2.2)과 같습니다.
사례 2: 하위 노드가 있음
이 상황도 처리가 매우 간단합니다. 삭제할 노드를 하위 노드로 교체한 다음 하위 노드를 삭제하면 됩니다. 마디. 위의 그림(2.3)과 같이
3번의 경우가 있는데, 두 개의 하위 노드
이 상황은 조금 복잡할 수 있습니다. 이를 대체하기 위해서는 삭제할 대체 노드(N)를 찾아 N을 삭제해야 한다. 크게 4가지 상황으로 나누어집니다. 1. N의 형제 노드 W는 빨간색 2. N의 남동생 W는 흑인이고, W의 두 자녀도 모두 흑인입니다. 3. N의 동생 w는 검정, w의 왼쪽 아이는 빨강, w의 오른쪽 아이는 빨강 아이는 흑인이다. 4. N의 남동생 w는 흑인이고, w의 오른쪽 아이는 빨갛다. 사례 3.1 N의 형제 노드 W는 빨간색 P도 검은색입니다. 처리 전략은 W와 P의 색상을 변경한 다음 왼쪽 회전을 수행하는 것입니다. 이 처리를 하면 빨간색과 검정색의 특성을 유지할 수 있습니다. N의 새 동생인 새 w는 로테이션 전의 w의 자식으로 흑인이다. 이 처리 후에 상황 3.1은 3.2, 3.3, 3.4 중 하나로 변환됩니다. 다음과 같습니다: 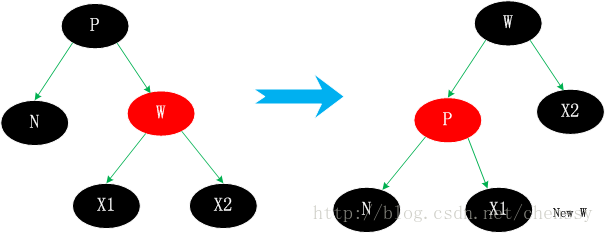
사례 3.2. N의 남동생 W는 흑인이고, W의 두 자녀도 모두 흑인이다.
이 경우 해당 상위 노드는 W가 검정색일 수 있으므로 N 하위 트리는 형제 W 하위 트리보다 검정색 노드가 하나 적습니다. 이때 W를 빨간색으로 설정할 수 있습니다. 이런 식으로 N 하위 트리와 W 하위 트리의 블랙 노드는 일관성을 유지하며 균형을 유지합니다. 다음과 같습니다

W를 검정색에서 빨간색으로 변환하면 새 노드 new N의 검정색 노드가 형제 노드보다 하나 적습니다. 그러나 새로운 x가 빨간색이면 전체 트리의 균형을 유지하기 위해 새로운 x를 검정색으로 직접 변환합니다. 그렇지 않으면 상황 3.2는 상황 3.1, 3.3, 3.4 중 하나로 변환됩니다.
사례 3.3 N 동생 w는 흑인, 왼쪽 w의 자식은 빨간색이고, w의 오른쪽 자식은 검은색입니다.
자식 노드는 색상 교환을 수행한 후 W에서 오른쪽 회전을 수행합니다.
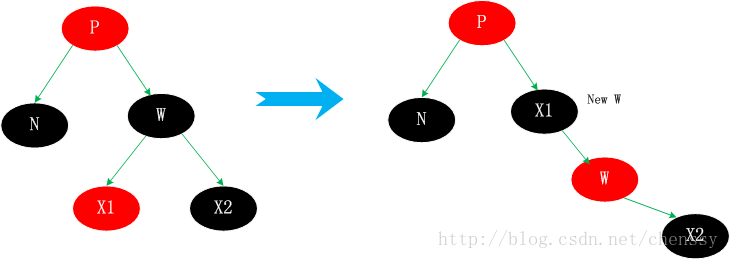
이때, N의 새 동생 X1(new w)은 빨간색 오른쪽 자식을 가진 블랙 노드이므로 상황 3은 상황 4로 변형됩니다.
사례 3.4 N의 동생은 흑인이고, w의 아이는 맞는 아이이다. 빨간색입니다.
W와 상위 노드의 색상 바꾸기 P 와 동시에 P 에 대해 왼쪽 회전 작업을 수행합니다. 그러면 왼쪽의 누락된 검은색 노드가 채워집니다. 동시에 W의 오른쪽 자식 노드 X2를 검정색으로 설정합니다. 이런 식으로 왼쪽과 오른쪽 사이의 균형이 이루어집니다. 总结 个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。 通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。 通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。 (1)除是寻找替代节点replacement,其实现方法为successor()。如下: (2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下: 1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。 2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。 3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。 删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。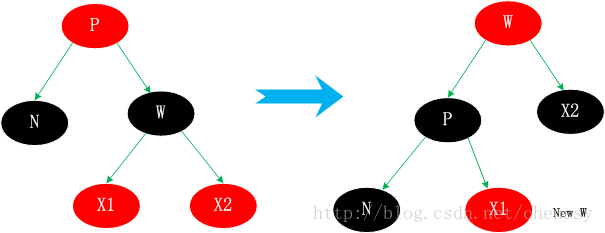
TreeMap deleteEntry()方法实现分析
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。
참으로 글이 좀 깁니다. 차분히 읽어주셔서 감사하다는 말씀 전하고 싶습니다. 이 블로그 게시물을 읽는 것은 꽤 보람 있는 일이 될 것입니다. 동시에, 이 블로그 게시물에서는 레드-블랙 트리의 구현 프로세스를 설명하는 데 많은 공간을 할애하고 Java의 TreeMap에 대해서는 덜 이야기합니다. 그러나 레드-블랙 트리의 구현 프로세스를 이해하면 다음과 같은 작업을 수행할 수 있다고 생각합니다. 케이크 조각인 TreeMap을 쉽게 마스터하세요.
동시에 이 블로그 글을 4일 동안 작성하면서 많은 내용을 읽고 참고했습니다. 블로그 게시물. 동시에 몇 가지 참고사항이 있을 수 밖에 없는데, 그분들께 감사의 말씀을 전하고 싶습니다. LZ는 2학년 때부터 자료구조를 배우기 시작했는데, 정말 잘했다고 생각했는데, 아직도 자료구조에 대해 배울 게 너무 많다는 걸 알게 되었어요. ! !
위 내용은 Java 개선편(27)의 내용입니다. -----TreeMap 관련 내용은 PHP 중국어 홈페이지(www.php.cn)를 참고해주세요. )!