MySQL의 InnoDB 인덱스 원리에 대한 자세한 설명-MySQL 튜토리얼-php.cn

요약:

이 글에서는 다양한 트리부터 인덱스 원리, 스토리지 세부 사항까지 Mysql의 InnoDB 인덱스와 관련된 지식을 소개합니다.

InnoDB는 Mysql의 기본 스토리지 엔진입니다(Mysql5.5.5 이전에는 MyISAM, 문서였습니다). 효율적인 학습을 위해 이 글에서는 주로 InnoDB를 소개하고, 비교를 위해 소량의 MyISAM을 사용했습니다.

이 글은 제가 공부하는 과정에서 요약한 내용입니다. (참고자료가 제공될 예정입니다.) 설명에 부정확한 내용이 있으면 지적해 주시기 바랍니다.

1 다양한 트리 구조

원래는 이미 인터넷에 관련 글이 너무 많아서 이진 검색 트리부터 시작할 생각은 없었지만, 명확한 일러스트레이션이 문제 이해 도움을 주고 기사의 완성도를 보장하기 위해 마침내 이 부분이 추가되었습니다.

먼저 여러 트리 구조를 살펴보겠습니다.

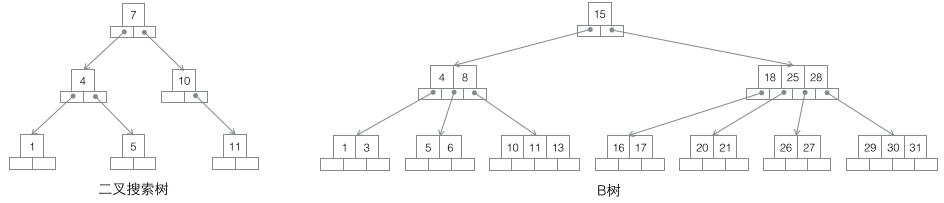
1 검색 이진 트리: 각 노드에는 두 개의 하위 노드가 있습니다. 데이터 양의 증가는 필연적으로 높이의 급격한 증가로 이어집니다. 이는 대용량 데이터 저장을 위한 인프라로는 적합하지 않습니다.

2 B-트리: m-차 B-트리는 균형 잡힌 m-방향 탐색 트리입니다. 가장 중요한 속성은 루트가 아닌 각 노드에 포함된 키워드 j의 수가 다음을 충족한다는 것입니다. ┌m/2┐ - 1

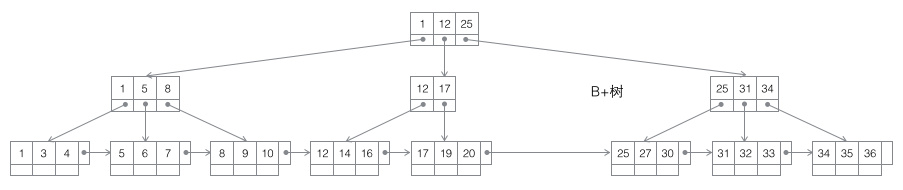
3 B+ 트리: m-차수 B-트리는 균형 잡힌 m-way 탐색 트리입니다. 가장 중요한 속성은 루트가 아닌 각 노드에 포함된 키워드 j의 수가 다음을 충족한다는 것입니다. ┌m/2┐ - 1

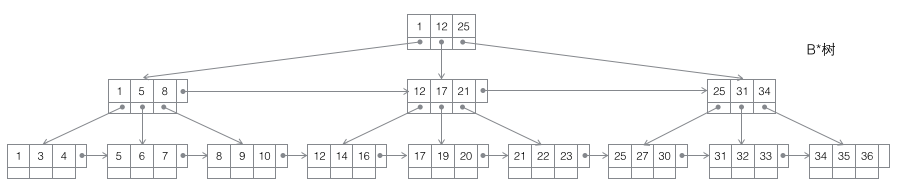
4 B* 트리: m-차수 B-트리는 균형 잡힌 m-방향 탐색 트리입니다. 가장 중요한 두 가지 속성은 1입니다. 각 비루트 노드에 포함된 키워드 j의 수는 다음을 충족합니다. ┌m2/3┐ - 1

　B/B+/B* 세 트리는 검색/삽입 등 유사한 작업을 수행합니다. /노드 삭제. 여기서 우리는 노드를 삽입하는 상황에만 초점을 맞추고 현재 노드가 가득 찼을 때만 삽입 작업을 분석합니다. 왜냐하면 이 작업은 약간 복잡하고 여러 트리 간의 차이점을 완전히 반영할 수 있기 때문입니다. 대조적으로, 노드 검색은 상대적으로 구현하기 쉬운 반면, 노드 삭제는 삽입의 역과정만 완료하면 됩니다(실제 응용에서 삭제는 삽입의 완전한 역순 작업이 아니며 데이터만 삭제되는 경우가 많으며 공간은 후속 작업을 위해 예약되어 있습니다). 사용).

먼저 B-트리의 분할을 살펴보겠습니다. 아래 그림에서 빨간색 값은 매번 새로 삽입되는 노드입니다. 노드가 가득 찰 때마다 분할이 발생해야 합니다(분할은 재귀 프로세스입니다. B-트리의 리프가 아닌 노드도 키를 저장하므로 아래 7의 삽입을 참조하세요). 값, 분할 후 전체 노드 값은 1. 원래 노드, 2. 원래 노드의 상위 노드, 3. 원래 노드의 새로운 형제 노드의 세 위치에 분산됩니다(참조 5와 7의 삽입 과정). 분할로 인해 트리의 높이가 증가할 수도 있고(3과 7의 삽입 과정 참조), 트리의 높이에 영향을 미치지 않을 수도 있습니다(5와 6의 삽입 과정 참조).

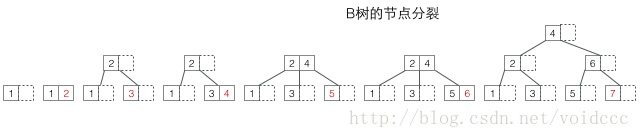
B+ 트리 분할: 노드가 가득 차면 새 노드를 할당하고 원래 노드에 있는 데이터의 1/2을 새 노드에 복사한 후 마지막으로 추가합니다. 부모 노드에 대한 새 노드의 포인터; B+ 트리의 분할은 원래 노드와 부모 노드에만 영향을 미치고 형제 노드에는 영향을 미치지 않으므로 형제 노드에 대한 포인터가 필요하지 않습니다.

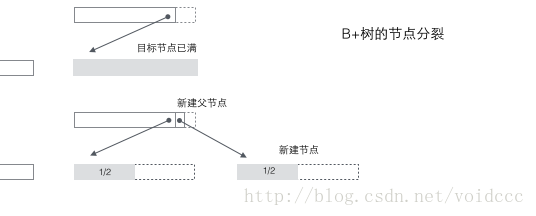
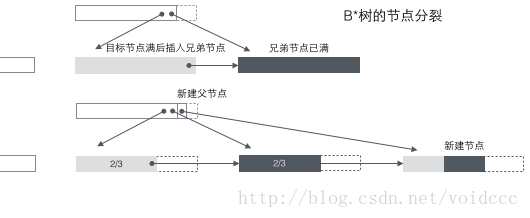
B* 트리 분할: 노드가 가득 찼을 때 다음 형제 노드가 가득 차지 않은 경우 데이터의 일부를 형제 노드로 이동한 다음 원래 노드에 키워드를 삽입하고 마지막으로 상위 노드를 수정합니다. 형제 노드의 키워드(형제 노드의 키워드 범위가 변경되었기 때문) 형제도 꽉 차 있으면 원래 노드와 형제 노드 사이에 새 노드를 추가하고 데이터의 1/3을 새 노드에 복사한 다음 마지막으로 새 노드의 포인터를 부모 노드에 추가합니다. B* 트리의 분할은 매우 영리하다는 것을 알 수 있습니다. 왜냐하면 B* 트리는 분할 노드가 여전히 2/3 가득 차 있는지 확인해야 하기 때문입니다. B+ 트리 방법을 사용하는 경우 전체 노드를 두 개로 나누기만 하면 됩니다. 각 노드는 1/2만 채워져 B* 트리의 요구 사항을 충족하지 않습니다. 따라서 B* 트리에서 채택한 전략은 현재 노드가 가득 찬 후에도 형제 노드를 계속 삽입하는 것입니다(이것이 B* 트리가 리프가 아닌 노드의 형제 간에 연결 목록을 추가해야 하는 이유입니다). 채워진 다음 형제 노드를 끌어와 함께 1/3을 기여하여 새 노드를 설정하면 3개의 노드가 정확히 2/3이 채워져 B* 트리의 요구 사항을 충족하게 됩니다. 그리고 모두가 행복해요.

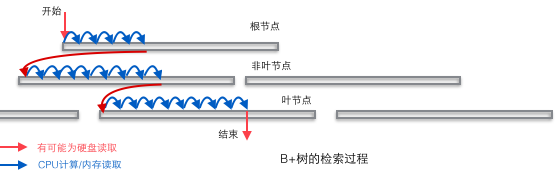
B+ 트리는 컴퓨터 메모리와 기계식 하드디스크의 2계층 저장 구조로 인해 전체적으로 데이터베이스의 기본 구조로 적합하다. 메모리는 빠른 랜덤 액세스(랜덤 액세스는 임의의 주소를 제공하고 이 주소에 저장된 데이터를 반환하도록 요청하는 것을 의미함)를 완료할 수 있지만 용량은 작습니다. 하드 디스크의 랜덤 액세스에는 기계적 동작(헤드 1회 이동, 디스크 2회전)이 필요하며 액세스 효율은 메모리에 비해 몇 자릿수 낮지만 하드 디스크의 용량은 더 큽니다. 일반적인 데이터베이스 용량은 사용 가능한 메모리 크기를 크게 초과하므로 B+ 트리에서 데이터 조각을 검색하려면 여러 디스크 IO 작업을 완료해야 할 가능성이 높습니다. 아래 그림과 같이: 일반적으로 노드를 읽는 작업은 디스크 IO 작업일 수 있지만 리프가 아닌 노드는 일반적으로 액세스 속도를 높이기 위해 초기 단계에서 메모리에 로드됩니다. 동시에, 노드 간 수평 순회 속도를 향상시키기 위해 그림의 파란색 CPU 계산/메모리 읽기는 실제 데이터베이스의 이진 검색 트리(InnoDB의 페이지 디렉터리 메커니즘)로 최적화될 수 있습니다.

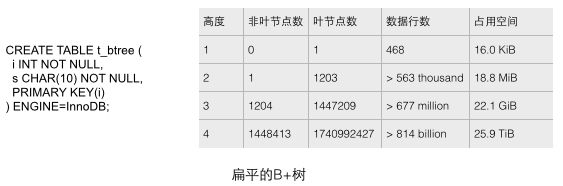
실제 데이터베이스의 B+ 트리는 매우 플랫해야 합니다. 테이블에 충분한 데이터를 순차적으로 삽입하면 InnoDB의 B+ 트리가 얼마나 플랫한지 확인할 수 있습니다. 아래와 같이 CREATE 문을 통해 간단한 필드만으로 테스트 테이블을 생성한 후 계속해서 데이터를 추가하여 이 테이블을 채웁니다. 아래 그림의 통계 데이터를 통해 여러 가지 직관적인 결론을 분석할 수 있습니다(출처는 참고 1 참조). 이러한 결론은 데이터베이스의 B+ 트리 규모를 거시적으로 보여줍니다.

　1 각 리프 노드는 468행의 데이터를 저장하고, 각 리프 노드는 약 1200개의 키 값을 저장합니다. 이것은 균형 잡힌 1200방향 검색 트리입니다!

　2 22.1G 용량의 테이블의 경우 높이가 3인 B+ 트리만 저장할 수 있습니다. 이 용량은 아마도 많은 애플리케이션의 요구를 충족할 수 있습니다. 높이를 4로 늘리면 B+트리의 저장 용량이 즉시 25.9T로 어마어마하게 늘어납니다!

　3 22.1G 용량의 테이블의 경우 B+ 트리의 높이는 3입니다. 리프가 아닌 모든 노드를 메모리에 로드하려면 18.8M 미만의 메모리가 필요합니다(어떻게 이 결론을 내리려면 높이가 2인 트리의 경우 1203개의 리프 노드가 18.8M 공간만 필요한 반면, 22.1G 보조 테이블의 높이는 3이고 동시에 1204개의 비리프 노드가 있기 때문입니다. 리프가 크기 때문에 리프 노드의 크기가 리프가 아닌 노드보다 크다고 가정합니다. 노드는 리프 노드 대신 행 데이터를 저장합니다(키와 소량의 데이터만 사용). 단 한 번의 디스크 IO 작업으로 필요한 데이터를 검색할 수 있도록 메모리를 확보하는 것은 매우 효율적입니다.

　2 Mysql 스토리지 엔진 및 인덱스

데이터베이스에는 인덱스가 있어야 한다고 할 수 있으며, 인덱스가 없으면 검색 과정은 순차 검색이 되며 O(n)의 시간 복잡도는 거의 견딜 수 없는. 키가 트리의 노드에 저장되어 있는 한, 단일 키로만 구성된 테이블이 B+ 트리를 사용하여 어떻게 인덱싱될 수 있는지 상상하기는 매우 쉽습니다. 데이터베이스 레코드에 여러 필드가 포함된 경우 B+ 트리는 기본 키가 아닌 필드를 검색하면 기본 키 인덱스가 해당 기능을 잃고 다시 순차 검색이 됩니다. 이때, 조회하려는 두 번째 컬럼에는 두 번째 인덱스 세트를 구축해야 한다. 이 인덱스는 독립적인 B+ 트리로 구성됩니다. 동일한 테이블 데이터 집합에 액세스하는 여러 B+ 트리 문제를 해결하는 두 가지 일반적인 방법이 있습니다. 하나는 클러스터형 인덱스(클러스터형 인덱스)라고 하고 다른 하나는 비클러스터형 인덱스(보조 인덱스)라고 합니다. 이 두 이름은 모두 인덱스라고 부르지만 별도의 인덱스 유형이 아니라 데이터 저장 방식이다. 클러스터형 인덱스 저장의 경우 행 데이터와 기본 키 B+ 트리가 함께 저장되며, 보조 키 B+ 트리는 보조 키만 저장하고 기본 키와 비기본 키 B+ 트리는 거의 두 가지 유형의 트리입니다. 비클러스터형 인덱스 저장소의 경우 기본 키 B+ 트리는 기본 키 대신 리프 노드의 실제 데이터 행에 대한 포인터를 저장합니다.

InnoDB는 기본 키를 B+ 트리로 구성하기 위해 클러스터형 인덱스를 사용하고, 행 데이터는 리프 노드에 저장됩니다. 기본 키를 찾기 위해 "where id = 14" 조건을 사용하는 경우 다음과 같습니다. B+ 트리 검색 알고리즘은 해당 리프 노드를 찾은 다음 행 데이터를 얻을 수 있습니다. Name 열에 대해 조건부 검색을 수행하는 경우 두 단계가 필요합니다. 첫 번째 단계는 보조 인덱스 B+ 트리에서 Name을 검색하고 해당 리프 노드에 도달하여 해당 기본 키를 얻는 것입니다. 두 번째 단계에서는 기본 키를 사용하여 기본 인덱스 B+ 트리 종에 대해 또 다른 B+ 트리 검색 작업을 수행하고 마지막으로 리프 노드에 도달하여 전체 데이터 행을 얻습니다.

MyISM은 비클러스터형 인덱스를 사용합니다. 비클러스터형 인덱스의 두 B+ 트리는 모양이 다르지 않습니다. 노드의 구조는 완전히 동일하지만 기본 키의 노드는 다릅니다. 인덱스 B+ 트리는 기본 키를 저장합니다. 인덱스 B+ 트리는 보조 키를 저장합니다. 테이블 데이터는 별도의 장소에 저장됩니다. 두 B+ 트리의 리프 노드는 주소를 사용하여 실제 테이블 데이터를 가리킵니다. 두 키 사이에는 차이가 없습니다. 인덱스 트리는 독립적이므로 보조 키를 통한 검색에는 기본 키에 대한 인덱스 트리에 대한 액세스가 필요하지 않습니다.

이 두 인덱스의 차이점을 좀 더 생생하게 표현하기 위해 아래와 같이 4행의 데이터를 저장하는 테이블을 상상해 보겠습니다. 그 중 Id는 1차 인덱스 역할을 하고, Name은 2차 인덱스 역할을 합니다. 다이어그램은 클러스터형 인덱스와 비클러스터형 인덱스의 차이점을 명확하게 보여줍니다.

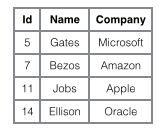
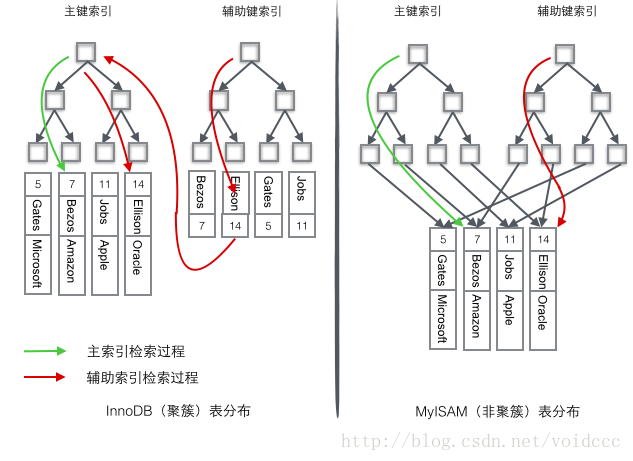
클러스터형 인덱스에 중점을 두는 것은 클러스터형 인덱스가 비클러스터형 인덱스에 비해 확실히 떨어지는 것 같습니다. 왜냐하면 보조 인덱스를 사용하여 검색할 때마다 두 번의 B+ 트리 검색이 필요하기 때문입니다. 클러스터형 인덱스의 장점은 무엇인가요?

1 행 데이터와 리프 노드가 함께 저장되므로 기본 키와 행 데이터가 함께 메모리에 로드됩니다. 리프 노드를 찾으면 데이터가 즉시 반환될 수 있습니다. 기본 키 ID에 따라 구성되어 데이터를 더 빠르게 얻을 수 있습니다.

　2 보조 인덱스는 주소 값을 포인터로 사용하는 대신 기본 키를 "포인터"로 사용하므로 행 이동이나 데이터 페이지 분할이 발생할 때 보조 인덱스의 유지 관리 작업을 줄일 수 있다는 장점이 있습니다. , 기본 키 값을 포인터로 사용하면 보조 인덱스가 더 많은 공간을 차지하게 됩니다. 이점은 행을 이동할 때 InnoDB가 보조 인덱스의 "포인터"를 업데이트할 필요가 없다는 것입니다. 즉, 데이터베이스의 데이터가 수정됨에 따라(이전 B+ 트리 노드 분할 및 페이지 분할) 행의 위치(구현 시 16K 페이지를 통해 위치, 이후에 설명)가 변경됩니다. 클러스터형 인덱스를 사용할 수 있습니다. 기본 키 B+ 트리의 노드가 어떻게 변경되더라도 보조 인덱스 트리는 영향을 받지 않습니다.

　 3페이지 구조

이전 콘텐츠가 원리를 설명하는 쪽으로 편향되어 있었다면 이후 콘텐츠에서는 구체적인 구현이 포함되기 시작합니다.

InnoDB의 구현을 이해하려면 페이지 구조를 언급해야 합니다. 페이지는 전체 InnoDB 스토리지의 가장 기본적인 구성 요소이자 InnoDB 디스크 관리의 가장 작은 단위입니다. 이 페이지 구조. 페이지는 여러 유형으로 구분됩니다. 일반적인 페이지 유형에는 데이터 페이지(B-tree Node), 실행 취소 페이지(Undo Log Page), 시스템 페이지(System Page), 트랜잭션 데이터 페이지(Transaction System Page) 등이 있습니다. 단일 페이지의 크기는 16K입니다(컴파일 매크로 UNIV_PAGE_SIZE에 의해 제어됨). 각 페이지는 32비트 int 값으로 고유하게 식별되며 이는 InnoDB의 최대 저장 용량인 64TB(16Kib * 2^32 = 64Tib)에 해당합니다. 페이지의 기본 구조는 다음과 같습니다.

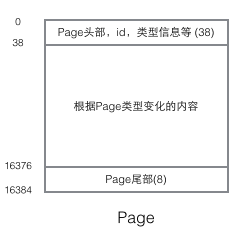
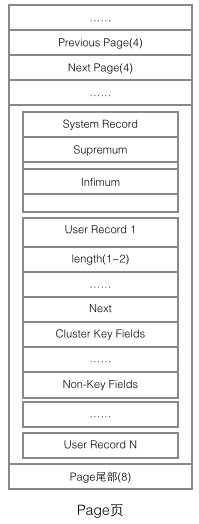
모든 페이지에는 공통된 머리와 꼬리가 있지만 페이지 유형에 따라 중간에 있는 내용이 달라집니다. 페이지 헤더에는 우리가 중요하게 생각하는 데이터가 있습니다. 다음 그림은 페이지 헤더의 세부 정보를 보여줍니다.

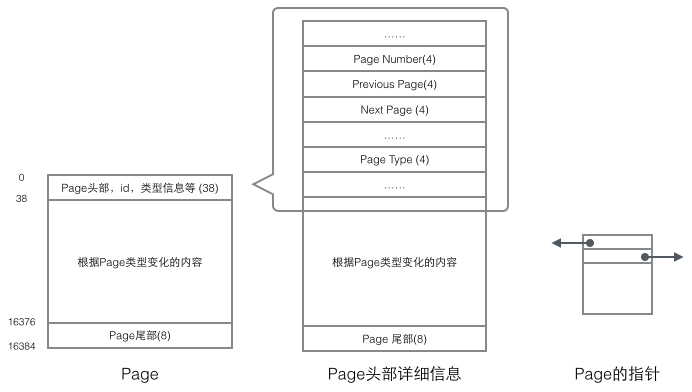
조직 구조와 관련된 데이터 필드: 페이지 헤더에는 이전 페이지와 다음 페이지를 각각 가리키는 두 개의 포인터가 저장됩니다. 헤더에는 페이지 유형 정보와 페이지를 고유하게 식별하는 데 사용되는 번호도 포함됩니다. 이 두 포인터를 기반으로 Page가 이중 연결 목록 구조로 연결되어 있음을 쉽게 상상할 수 있습니다.

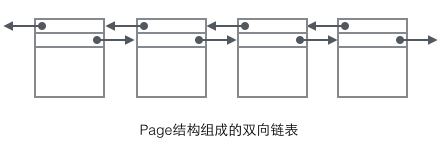
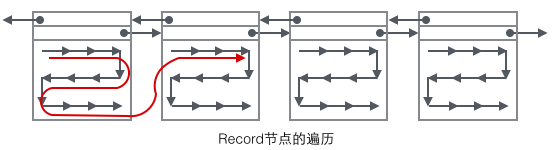
페이지의 주요 내용을 살펴보면 주로 행 데이터와 인덱스의 저장에 중점을 두고 있습니다. 모두 페이지의 사용자 기록 섹션에 있습니다. 레코드는 페이지 공간의 대부분을 차지하며, 사용자 레코드는 하나씩 레코드로 구성되며 각 레코드는 인덱스 트리의 노드(비리프 노드 및 리프 노드)를 나타냅니다. 페이지 내에서 단일 연결 목록의 헤드와 테일은 고정된 내용을 포함하는 두 개의 레코드로 표시됩니다. 문자열 형식의 "Infimum"은 시작을 나타내고 "Supremum"은 끝을 나타냅니다. 시작과 끝을 나타내는 데 사용되는 이 두 레코드는 시스템 레코드 세그먼트에 저장됩니다. 시스템 레코드와 사용자 레코드는 두 개의 병렬 세그먼트입니다. InnoDB에는 기본 키 인덱스 트리 비리프 노드 1개, 기본 키 인덱스 트리 리프 노드 2개, 보조 키 인덱스 트리 비리프 노드 3개, 보조 키 인덱스 트리 리프 노드 4개 등 4개의 서로 다른 레코드가 있습니다. 이 네 노드의 레코드 형식에는 약간의 차이가 있지만 모두 다음 레코드를 가리키는 Next 포인터를 저장합니다. 나중에 이 네 가지 유형의 노드를 자세히 소개하겠습니다. 지금은 Record를 데이터를 저장하고 Next 포인터를 포함하는 단일 연결 목록 노드로 취급하면 됩니다.

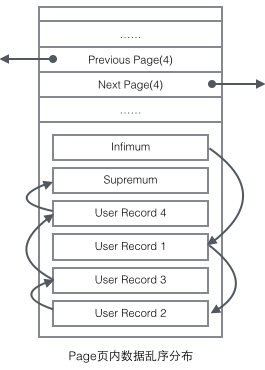
페이지에 사용자 레코드가 단일 연결 목록 형태로 존재합니다. 처음에는 삽입된 순서대로 데이터가 정렬되지만, 새로운 데이터가 삽입되고 오래됩니다. 데이터가 삭제되면 데이터의 물리적 순서는 혼란스러워지지만 여전히 논리적 순서를 유지합니다.

사용자 기록의 정리 형태를 여러 페이지와 결합하면 조금은 완성된 형태를 볼 수 있습니다.

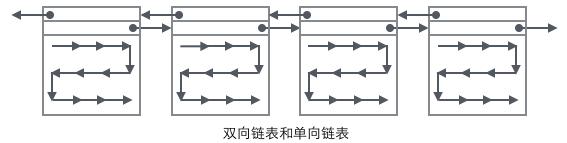
이제 레코드를 찾는 방법을 살펴보겠습니다.

1. 루트 노드를 통해 인덱스된 B+ 트리 탐색을 시작하고 마지막으로 인덱스된 B+ 트리에 도달합니다. 각 수준의 리프가 아닌 노드를 통해 트리를 생성하면 모든 리프 노드가 이 페이지에 저장됩니다.

　2 페이지의 "Infimum" 노드에서 시작하여 단일 연결 목록을 탐색하고(이 탐색은 종종 최적화됨) 키를 찾으면 성공적으로 반환합니다. 레코드가 "supremum"에 도달하면 현재 페이지에 적합한 키가 없다는 의미입니다. 이때 페이지의 다음 페이지 포인터를 사용하여 다음 페이지로 이동하고 처음부터 하나씩 계속 검색해야 합니다. "인피멈".

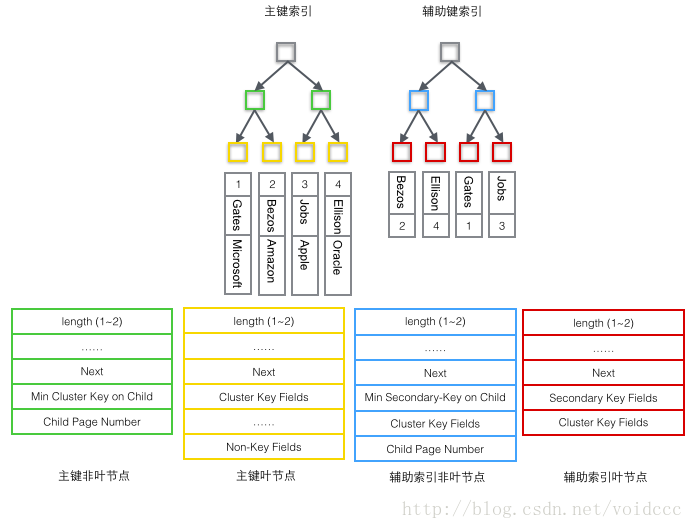
다양한 B+ 트리 노드에 따라 어떤 데이터가 저장되는지 자세히 살펴보겠습니다. 사용자 레코드는 그림과 같이 4가지 형식으로 나눌 수 있습니다. 아래 그림에서는 색상에 따라 구분됩니다.

　1 메인 인덱스 트리의 리프가 아닌 노드(녹색)

　1 자식 노드에 저장된 기본 키 중 가장 작은 값(Min Cluster Key on Child ), 이것은 B+ 트리입니다. 필수이며, 해당 기능은 페이지에서 특정 레코드 위치를 찾는 것입니다.

　2 레코드를 찾는 데 사용되는 가장 작은 값이 있는 페이지 번호(하위 페이지 번호)입니다.

　2개의 기본 인덱스 트리 리프 노드(노란색)

　1 기본 키(클러스터 키 필드), B+ 트리에 필요하며 데이터 행의 일부임

2 기본 키를 제외한 데이터 행의 다른 모든 열 집합인 기본 키(Non-Key Fields)를 제외한 모든 열입니다.

여기서 두 부분 1과 2를 합하면 완전한 데이터 행이 됩니다.

　3 보조 인덱스 트리 비리프 노드 비(파란색)

　1 자식 노드에 저장된 보조 키 값 중 최소값(Min Secondary- Key on Child)는 B+ 트리에 필요한 기능으로 페이지에서 특정 레코드 위치를 찾는 것입니다.

　2 기본키 값(클러스터 키 필드), 리프가 아닌 노드는 왜 기본키를 저장하는 걸까요? 보조 인덱스는 고유하지 않을 수 있지만 B+ 트리에서는 키 값이 고유해야 하므로 여기서 보조 키의 값과 기본 키의 값을 결합하여 B+ 트리의 실제 키 값으로, 독특함을 보장합니다. 그러나 이로 인해 보조 인덱스 B+ 트리의 리프가 아닌 노드가 리프 노드보다 4바이트 더 많아지게 됩니다. (즉, 아래 그림의 파란색 노드는 빨간색 노드보다 4바이트 더 많습니다)

　3 레코드를 찾는 데 사용되는 가장 작은 값이 있는 페이지 번호(하위 페이지 번호)입니다.

　4개의 보조 인덱스 트리 리프 노드(빨간색)

　1 B+ 트리에 필요한 보조 인덱스 키 값(보조 키 필드)입니다.

　2 기본 키 값(Cluster Key Fields), 전체 레코드를 찾기 위해 메인 인덱스 트리에서 또 다른 B+ 트리 검색을 수행하는 데 사용됩니다.

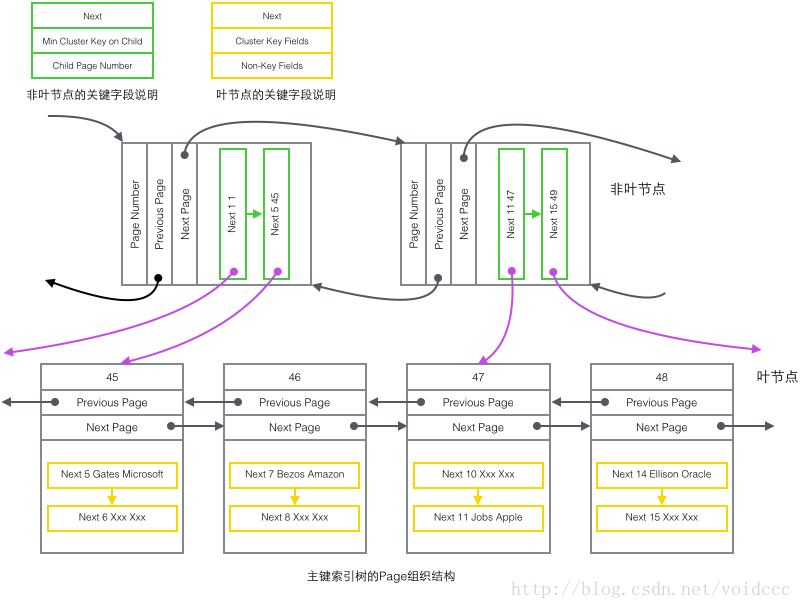
이 글에서 가장 중요한 부분은 B+ 트리의 구조와 앞서 소개한 4가지 레코드 유형의 내용을 결합하면 최종적으로 다음과 같다. 파노라마 사진. 보조 인덱스의 B+ 트리는 기본 키 인덱스와 유사한 구조를 가지므로 여기에는 기본 키 인덱스 트리의 구조 다이어그램만 그려져 있습니다. 여기에는 "기본 키 비리프 노드"와 ""라는 두 가지 유형의 노드만 포함됩니다. 기본 키 리프 노드"는 위 그림의 두 가지 유형의 노드입니다. 녹색과 노란색 부분입니다.

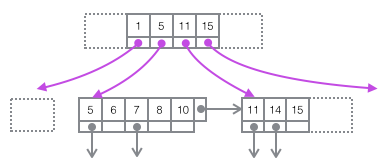
위 그림을 아래의 보다 간결한 트리 다이어그램으로 복원합니다. 이것은 B+ 트리의 일부입니다. 페이지와 B+ 트리 노드 사이에는 일대일 대응이 없습니다. 페이지는 레코드 저장 컨테이너로만 사용됩니다. 위 그림의 47페이지는 트리에 있습니다. 구조는 두 개의 독립적인 노드로 분할됩니다.