Python에서 목록의 중앙값을 얻는 방법

소개

중앙값은 집합의 값을 상하위 부분을 동일하게 나눈 값입니다. 목록 데이터의 개수가 홀수이면 목록 중앙에 있는 데이터가 목록 데이터의 중앙값이 되고, 목록 데이터의 개수가 짝수이면 목록 중앙에 있는 두 데이터의 산술 평균이 됩니다. 목록은 목록 데이터의 중앙값입니다. 이 작업에서는 자연수를 포함하는 비어 있지 않은 배열(X)이 제공됩니다. 상하로 나누어 중앙값을 구해야 합니다.

입력: 정수(int) 목록을 배열로 반환합니다.

출력: 배열의 중앙값(int, float).

예

get_median([1, 2, 3, 4, 5]) == 3
get_median([3, 1, 2, 5, 3]) == 3
get_median([1, 300, 2, 200, 1]) == 2
get_median([3, 6, 20, 99, 10, 15]) == 12.5

사용방법: 중위수는 확률론, 통계학에서 사용되며, 편향된 분포를 가지고 있습니다. 놀라운 가치입니다. 예를 들어, 우리는 일련의 데이터에서 사람들의 평균 부를 알고 싶습니다. 100명은 한 달에 100달러를 벌고, 10명은 한 달에 100만 달러를 벌고 있습니다. 평균을 계산하면 91,000달러가 나옵니다. 이는 실제로 무슨 일이 일어나고 있는지 전혀 보여주지 않는 이상한 값입니다. 따라서 이 경우 중앙값은 더 유용한 값과 더 나은 설명을 제공합니다.

전제 조건:<code><strong> </strong>1 < len(data) ≤ 1000 all(0 ≤ x < 10 ** 6 for x in data)

1 < len(data) ≤ 1000 all(0 ≤ x < 10 ** 6 for x in data)

일반적인 방법:

목록을 정렬하고 목록 길이가 홀수인지 짝수인지에 따라 중앙값을 계산합니다.

def get_median(data):
   data = sorted(data)
   size = len(data)
   if size % 2 == 0: # 判断列表长度为偶数
    median = (data[size//2]+data[size//2-1])/2
    data[0] = median
   if size % 2 == 1: # 判断列表长度为奇数
    median = data[(size-1)//2]
    data[0] = median
   return data[0]

가장 좋은 방법:

이 솔루션은 매우 영리합니다. 역의 합이 1이라는 속성을 갖고 목록의 음수 인덱스를 통해 목록의 중앙값을 얻습니다.

return (data[half] + data[~half]) / 2

설명:

정렬하면 [1,2,3,4,5,6]의 수열을 구하고, 목록 길이는 짝수의 경우 목록의 두 중간 요소인 3(인덱스 2)과 4(인덱스 3)에 의해 중앙값이 결정됩니다. 요소 4의 음수 인덱스는 -3이며 이는 정확히 인덱스 2의 반대입니다.

정렬 후 시퀀스 [1,2,3,4,5]가 얻어집니다. 목록 길이는 홀수이고 중앙값은 목록의 중간 요소 3(인덱스는 2)에 의해 결정됩니다. , 음수 지수는 -3입니다). 여전히 코드를 준수합니다.

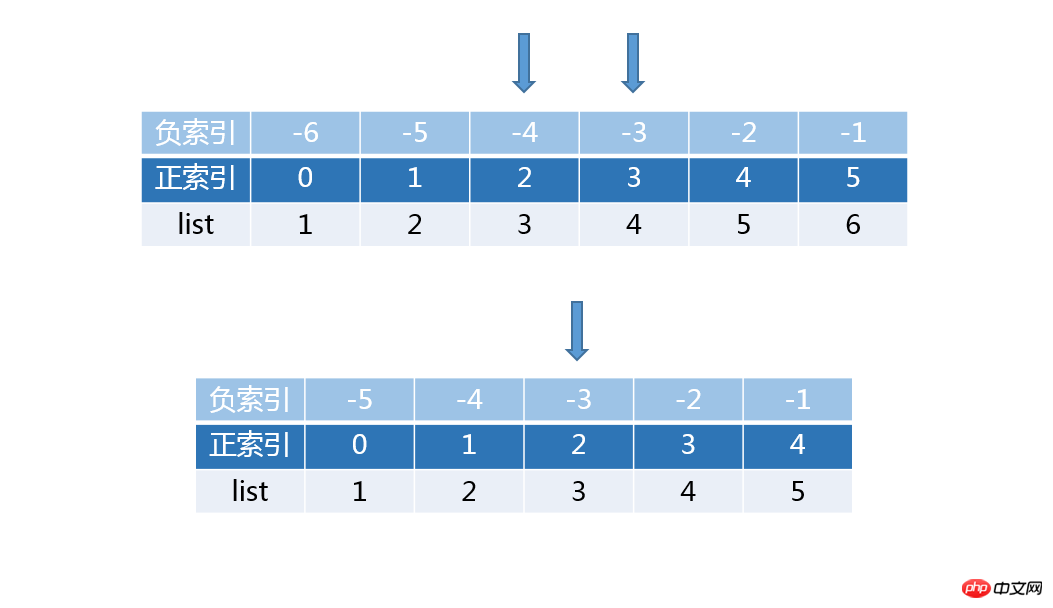
   def get_median(data):
   data.sort()
   half = len(data) // 2
   return (data[half] + data[~half]) / 2

Python에서 목록(List)의 중앙값을 구하는 방법에 대한 더 많은 기사를 보려면 PHP 중국어 웹사이트에 주목하세요!