本篇是给大家介绍的python实现解析树以及实现二叉树的三种遍历,先序遍历,中序遍历,后序遍历的例子,非常的详细,有需要的小伙伴可以参考下。
解析树
完成树的实现之后,现在我们来看一个例子,告诉你怎么样利用树去解决一些实际问题。在这个章节,我们来研究解析树。解析树常常用于真实世界的结构表示,例如句子或数学表达式。
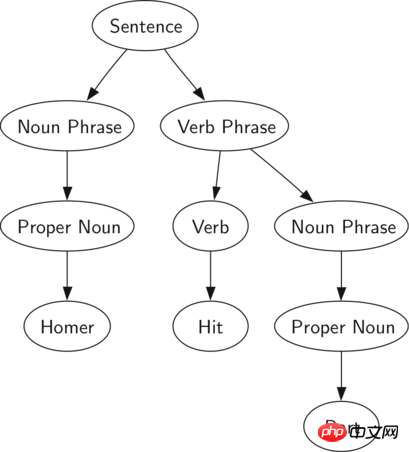
图 1:一个简单句的解析树
立即学习“Python免费学习笔记(深入)”;
图 1 显示了一个简单句的层级结构。将一个句子表示为一个树,能使我们通过利用子树来处理句子中的每个独立的结构。
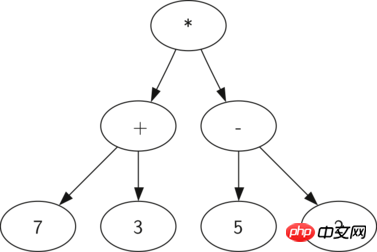
图 2: ((7+3)*(5−2)) 的解析树
如图 2 所示,我们能将一个类似于 ((7+3)*(5−2)) 的数学表达式表示出一个解析树。我们已经研究过全括号表达式,那么我们怎样理解这个表达式呢?我们知道乘法比加或者减有着更高的优先级。因为括号的关系,我们在做乘法运算之前,需要先计算括号内的加法或者减法。树的层级结构帮我们理解了整个表达式的运算顺序。在计算最顶上的乘法运算前,我们先要计算子树中的加法和减法运算。左子树的加法运算结果为 10,右子树的减法运算结果为 3。利用树的层级结构,一旦我们计算出了子节点中表达式的结果,我们能够将整个子树用一个节点来替换。运用这个替换步骤,我们得到一个简单的树,如图 3 所示。
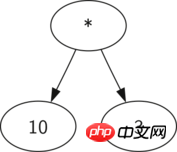
图 3: ((7+3)*(5−2)) 的化简后的解析树
在本章的其余部分,我们将更加详细地研究解析树。尤其是:
怎样根据一个全括号数学表达式来建立其对应的解析树
怎样计算解析树中数学表达式的值
怎样根据一个解析树还原数学表达式
建立解析树的第一步,将表达式字符串分解成符号保存在列表里。这里有四种符号需要我们考虑:左括号,操作符和操作数。我们知道读到一个左括号时,我们将开始一个新的表达式,因此我们创建一个子树来对应这个新的表达式。相反,每当我们读到一个右括号,我们就得结束这个表达式。另外,操作数将成为叶节点和他们所属的操作符的子节点。最后,我们知道每个操作符都应该有一个左子节点和一个右子节点。通过上面的分析我们定义以下四条规则:
如果当前读入的字符是'(',添加一个新的节点作为当前节点的左子节点,并下降到左子节点处。
如果当前读入的字符在列表['+', '-', '/', '*']中,将当前节点的根值设置为当前读入的字符。添加一个新的节点作为当前节点的右子节点,并下降到右子节点处。
如果当前读入的字符是一个数字,将当前节点的根值设置为该数字,并返回到它的父节点。
如果当前读入的字符是')',返回当前节点的父节点。
在我们编写 Python 代码之前,让我们一起看一个上述的例子。我们将使用 (3+(4*5))
这个表达式。我们将表达式分解为如下的字符列表:['(', '3', '+', '(', '4', '*', '5' ,')',')']。一开始,我们从一个仅包括一个空的根节点的解析树开始。如图 4,该图说明了随着每个新的字符被读入后该解析树的内容和结构。

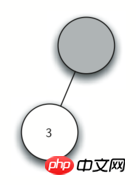
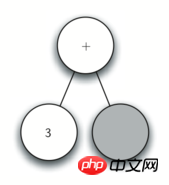
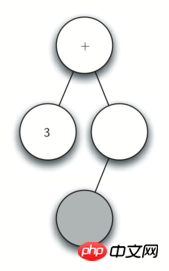
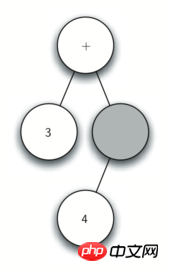
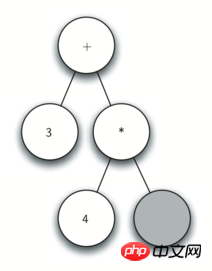
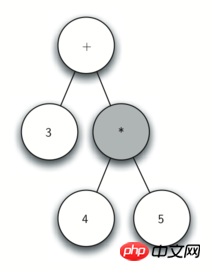
图 4:解析树结构的步骤图
观察图 4,让我们一步一步地过一遍:
创建一个空的树。
读如(作为第一个字符,根据规则 1,创建一个新的节点作为当前节点的左子结点,并将当前节点变为这个新的子节点。
读入3作为下一个字符。根据规则 3,将当前节点的根值赋值为3然后返回当前节点的父节点。
读入+作为下一个字符。根据规则 2,将当前节点的根值赋值为+,然后添加一个新的节点作为其右子节点,并且将当前节点变为这个新的子节点。
读入(作为下一个字符。根据规则 1,创建一个新的节点作为当前节点的左子结点,并将当前节点变为这个新的子节点。
读入4作为下一个字符。根据规则 3,将当前节点的根值赋值为4然后返回当前节点的父节点
读入*作为下一个字符。根据规则 2,将当前节点的根值赋值为*,然后添加一个新的节点作为其右子节点,并且将当前节点变为这个新的子节点。
读入5作为下一个字符。根据规则 3,将当前节点的根值赋值为5然后返回当前节点的父节点
读入)作为下一个字符。根据规则 4,我们将当前节点变为当前节点*的父节点。
读入)作为下一个字符。根据规则 4,我们将当前节点变为当前节点+的父节点,因为当前节点没有父节点,所以我们已经完成解析树的构建。
通过上面给出的例子,很明显我们需要跟踪当前节点和当前节点的父节点。树提供给我们一个获得子节点的方法——通过getLeftChild和getRightChild方法,但是我们怎么样来跟踪一个节点的父节点呢?一个简单的方法就是在我们遍历整个树的过程中利用栈跟踪父节点。当我们想要下降到当前节点的子节点时,我们先将当前节点压入栈。当我们想要返回当前节点的父节点时,我们从栈中弹出该父节点。
通过上述的规则,使用栈和二叉树来操作,我们现在编写函数来创建解析树。解析树生成函数的代码如下所示。
from pythonds.basic.stack import Stack
from pythonds.trees.binaryTree import BinaryTree
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('')
pStack.push(eTree)
currentTree = eTree
for i in fplist:
if i == '(':
currentTree.insertLeft('')
pStack.push(currentTree)
currentTree = currentTree.getLeftChild()
elif i not in ['+', '-', '*', '/', ')']:
currentTree.setRootVal(int(i))
parent = pStack.pop()
currentTree = parent
elif i in ['+', '-', '*', '/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')':
currentTree = pStack.pop()
else:
raise ValueError
return eTree
pt = buildParseTree("( ( 10 + 5 ) * 3 )")
pt.postorder() #defined and explained in the next section这四条建立解析树的规则体现在四个if从句,它们分别在第 11,15,19,24 行。如上面所说的,在这几处你都能看到规则的代码实现,并需要调用一些BinaryTree和Stack的方法。这个函数中唯一的错误检查是在else语句中,一旦我们从列表中读入的字符不能辨认,我们就会报一个ValueError的异常。现在我们已经建立了一个解析树,我们能用它来干什么呢?第一个例子,我们写一个函数来计算解析树的值,并返回该计算的数字结果。为了实现这个函数要利用树的层级结构。重新看一下图 2,回想一下我们能够将原始的树替换为简化后的树(图 3)。这提示我们写一个通过递归计算每个子树的值来计算整个解析树的值。
就像我们以前实现递归算法那样,我们将从基点来设计递归计算表达式值的函数。这个递归算法的自然基点是检查操作符是否为叶节点。在解析树中,叶节点总是操作数。因为数字变量如整数和浮点数不需要更多的操作,这个求值函数只需要简单地返回叶节点中存储的数字就可以。使函数走向基点的递归过程就是调用求值函数计算当前节点的左子树、右子树的值。递归调用使我们朝着叶节点,沿着树下降。
为了将两个递归调用的值整合在一起,我们只需简单地将存在父节点中的操作符应用到两个子节点返回的结果。在图 3 中,我们能看到两个子节点的值,分别为 10 和 3。对他们使用乘法运算得到最终结果 30。
递归求值函数的代码如 Listing1 所示,我们得到当前节点的左子节点、右子节点的参数。如果左右子节点的值都是 None,我们就能知道这个当前节点是一个叶节点。这个检查在第 7 行。如果当前节点不是一个叶节点,查找当前节点的操作符,并用到它左右孩子的返回值上。
为了实现这个算法,我们使用了字典,键值分别为'+','-','*'和'/'。存在字典里的值是 Python 的操作数模块中的函数。这个操作数模块为我们提供了很多常用函数的操作符。当我们在字典中查找一个操作符时,相应的操作数变量被取回。既然是函数,我们可以通过调用函数的方式来计算算式,如function(param1,param2)。所以查找opers['+'](2,2)就等价于operator.add(2,2)。
Listing 1
def evaluate(parseTree):
opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truep}
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC:
fn = opers[parseTree.getRootVal()]
return fn(evaluate(leftC),evaluate(rightC))
else:
return parseTree.getRootVal()最后,我们将在图 4 中创建的解析树上遍历求值。当我们第一次调用求值函数时,我们传递解析树参数parseTree,作为整个树的根。然后我们获得左右子树的引用来确保它们一定存在。递归调用在第 9 行。我们从查看树根中的操作符开始,这是一个'+'。这个'+'操作符找到operator.add函数调用,且有两个参数。通常对一个 Python 函数调用而言,Python 第一件做的事情就是计算传给函数的参数值。通过从左到右的求值过程,第一个递归调用从左边开始。在第一个递归调用中,求值函数用来计算左子树。我们发现这个节点没有左、右子树,所以我们在一个叶节点上。当我们在叶节点上时,我们仅仅是返回这个叶节点存储的数值作为求值函数的结果。因此我们返回整数 3。
现在,为了顶级调用operator.add函数,我们计算好其中一个参数了,但我们还没有完。继续从左到右计算参数,现在递归调用求值函数用来计算根节点的右子节点。我们发现这个节点既有左节点又有右节点,所以我们查找这个节点中存储的操作符,是'*',然后调用这个操作数函数并将它的左右子节点作为函数的两个参数。此时再对它的两个节点调用函数,这时发现它的左右子节点是叶子,分别返回两个整数 4 和 5。求出这两个参数值后,我们返回operator.mul(4,5)的值。此时,我们已经计算好了顶级操作符'+'的两个操作数了,所有需要做的只是完成调用函数operator.add(3,20)即可。这个结果就是整个表达式树 (3+(4*5)) 的值,这个值是 23。
树的遍历
之前我们已经了解了树的基本功能,现在我们来看一些应用模式。按照节点的访问方式不同,模式可分为 3 种。这三种方式常被用于访问树的节点,它们之间的不同在于访问每个节点的次序不同。我们把这种对所有节点的访问称为遍历(traversal)。这三种遍历分别叫做先序遍历(preorder),中序遍历(inorder)和后序遍历(postorder)。我们来给出它们的详细定义,然后举例看看它们的应用。
先序遍历
在先序遍历中,我们先访问根节点,然后递归使用先序遍历访问左子树,再递归使用先序遍历访问右子树。
中序遍历
在中序遍历中,我们递归使用中序遍历访问左子树,然后访问根节点,最后再递归使用中序遍历访问右子树。
后序遍历
在后序遍历中,我们先递归使用后序遍历访问左子树和右子树,最后访问根节点。
现在我们用几个例子来说明这三种不同的遍历。首先我们先看看先序遍历。我们用树来表示一本书,来看看先序遍历的方式。书是树的根节点,每一章是根节点的子节点,每一节是章节的子节点,每一小节是每一章节的子节点,以此类推。图 5 是一本书只取了两章的一部分。虽然遍历的算法适用于含有任意多子树的树结构,但我们目前为止只谈二叉树。

图 5:用树结构来表示一本书
设想你要从头到尾阅读这本书。先序遍历恰好符合这种顺序。从根节点(书)开始,我们按照先序遍历的顺序来阅读。我们递归地先序遍历左子树,在这里是第一章,我们继续递归地先序遍历访问左子树第一节 1.1。第一节 1.1 没有子节点,我们不再递归下去。当我们阅读完 1.1 节后我们回到第一章,这时我们还需要递归地访问第一章的右子树 1.2 节。由于我们先访问左子树,我们先看 1.2.1 节,再看 1.2.2 节。当 1.2 节读完后,我们又回到第一章。之后我们再返回根节点(书)然后按照上述步骤访问第二章。
由于用递归来编写遍历,先序遍历的代码异常的简洁优雅。Listing 2 给出了一个二叉树的先序遍历的 Python 代码。
Listing 2
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())我们也可以把先序遍历作为BinaryTree类中的内置方法,这部分代码如 Listing 3 所示。注意这一代码从外部移到内部所产生的变化。一般来说,我们只是将tree换成了self。但是我们也要修改代码的基点。内置方法在递归进行先序遍历之前必须检查左右子树是否存在。
Listing 3
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()内置和外置方法哪种更好一些呢?一般来说preorder作为一个外置方法比较好,原因是,我们很少是单纯地为了遍历而遍历,这个过程中总是要做点其他事情。事实上我们马上就会看到后序遍历的算法和我们之前写的表达式树求值的代码很相似。只是我们接下来将按照外部函数的形式书写遍历的代码。后序遍历的代码如 Listing 4 所示,它除了将print语句移到末尾之外和先序遍历的代码几乎一样。
Listing 4
def postorder(tree):
if tree != None:
postorder(tree.getLeftChild())
postorder(tree.getRightChild())
print(tree.getRootVal())我们已经见过了后序遍历的一般应用,也就是通过表达式树求值。我们再来看 Listing 1,我们先求左子树的值,再求右子树的值,然后将它们利用根节点的运算连在一起。假设我们的二叉树只存储表达式树的数据。我们来改写求值函数并尽量模仿后序遍历的代码,如 Listing 5 所示。
Listing 5
def postordereval(tree):
opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truep}
res1 = None
res2 = None
if tree:
res1 = postordereval(tree.getLeftChild())
res2 = postordereval(tree.getRightChild())
if res1 and res2:
return opers[tree.getRootVal()](res1,res2)
else:
return tree.getRootVal()我们发现 Listing 5 的形式和 Listing 4 是一样的,区别在于 Listing 4 中我们输出键值而在 Listing 5 中我们返回键值。这使我们可以通过第 6 行和第 7 行将递归得到的值存储起来。之后我们利用这些保存起来的值和第 9 行的表达式0一起运算。
在这节的最后我们来看看中序遍历。在中序遍历中,我们先访问左子树,之后是根节点,最后访问右子树。 Listing 6 给出了中序遍历的代码。我们发现这三种遍历的函数代码只是调换了输出语句的位置而不改动递归语句。
Listing 6
def inorder(tree): if tree != None: inorder(tree.getLeftChild()) print(tree.getRootVal()) inorder(tree.getRightChild())
当我们对一个解析树作中序遍历时,得到表达式的原来形式,没有任何括号。我们尝试修改中序遍历的算法使我们得到全括号表达式。只要做如下修改:在递归访问左子树之前输出左括号,然后在访问右子树之后输出右括号。修改的代码见 Listing 7。
Listing 7
def printexp(tree):
sVal = ""
if tree:
sVal = '(' + printexp(tree.getLeftChild())
sVal = sVal + str(tree.getRootVal())
sVal = sVal + printexp(tree.getRightChild())+')'
return sVal我们发现printexp函数对每个数字也加了括号,这些括号显然没必要加。
以上就是图文详解Python解析树及树的遍历的详细内容,更多请关注php中文网其它相关文章!

python怎么学习?python怎么入门?python在哪学?python怎么学才快?不用担心,这里为大家提供了python速学教程(入门到精通),有需要的小伙伴保存下载就能学习啦!

Copyright 2014-2025 https://www.php.cn/ All Rights Reserved | php.cn | 湘ICP备2023035733号