세 가지 무한 분류 방식(반복, 재귀, 참조)
일반적인 분류 트리 구조는 두 가지가 있습니다.
하나는 인접 리스트(adjacency list)로 id와 parent id의 형태입니다.
다른 하나는 중첩된 set으로, 왼쪽 값과 오른쪽 값의 형태입니다.
왼쪽 및 오른쪽 값 형식쿼리가 더 효율적이고 재귀 등이 필요하지 않습니다. 권장되지만 그렇지 않습니다. pid 형식만큼 간단하고 직관적이며 다소 오래되었습니다. 지역과 유사한 데이터베이스의 구조 설계는 항상 pid 형식이었습니다(둘을 변환할 수 있는 알고리즘이 있는 것 같지만 저는 가지 않겠습니다. 세부적으로) 그렇습니다. . .
다음은 모두 인접 리스트 형식입니다. 테이블 은 id, pid, name 형식과 유사합니다.
일반적으로 이는 데이터베이스에서 모든 데이터를 읽은 다음 배열 을 조합하여 수행됩니다. 물론 재귀적일 때마다 데이터베이스를 쿼리할 수도 있지만 그렇게 됩니다. 데이터베이스에 압력을 가할 수 있으며 메서드로 캡슐화하기가 쉽지 않아 권장되지 않습니다.
현재 일반적으로 사용되는 세 가지 방법이 있습니다. 선택 드롭다운 메뉴 표시 스타일을 구현해 보겠습니다.
첫 번째는 가장 일반적으로 사용되는 방법입니다. 또한 가장 효율적이지 않은 방법입니다. foreachloop를 재귀적으로 유지하세요.
function getTreeOptions3($list, $pid = 0)
{ $options = []; foreach ($list as $key => $value) { if ($value['id'] == $pid) {//查看是否为子元素,如果是则递归继续查询
$options[$value['id']] = $value['name']; unset($list[$key]);//销毁已查询的,减轻下次递归时查询数量
$optionsTmp = $this->getTreeOptions3($list, $value['id']);//递归
if (!empty($optionsTmp)) { $options = array_merge($options, $optionsTmp);
}
}
} return $options;
}2. 두 번째 방법은 스택에 push하고 pop하는 재귀를 사용하여 계산하는 것보다 효율성이 좋습니다. 이전 버전이지만 속도도 상당히 느립니다. 프로세스는 먼저 배열을 뒤집은 다음 최상위 배열을 꺼내 스택에 푸시하고 while 루프를 시작한 다음 먼저 스택에서 하나를 팝하여 하위 노드가 있는지 확인하는 것입니다. 그리고 하위 노드가 있으면 이 하위 노드도 스택에 푸시합니다. 다음 while 루프는 하위 노드를 확인하는 등의 작업을 수행합니다.
function getTreeOptions2($list, $pid = 0)
{ $tree = []; if (!empty($list)) { //先将数组反转,因为后期出栈时会优先出最上面的
$list = array_reverse($list); //先取出顶级的来压入数组$stack中,并将在$list中的删除掉
$stack = []; foreach ($list as $key => $value) { if ($value['pid'] == $pid) { array_push($stack,$value); unset($list[$key]);
}
} while (count($stack)) { //先从栈中取出第一项
$info = array_pop($stack); //查询剩余的$list中pid与其id相等的,也就是查找其子节点
foreach ($list as $key => $child) { if ($child[pid] == $info['id']) { //如果有子节点则入栈,while循环中会继续查找子节点的下级
array_push($stack, $child); unset($list[$key]);
}
} //组装成下拉菜单格式
$tree[$info['id']] = $info['name'];
}
} return $tree;
}
3. 을 사용하여 처리를 인용하세요. 이는 정말 영리하고 가장 효율적입니다. 여기를 참조하세요.
/**
* 先生成类似下面的形式的数据
* [
* 'id'=>1,
* 'pid'=>0,
* 'items'=>[
* 'id'=>2,
* 'pid'=>'1'
* 。。。
* ]
* ]*/function getTree($list, $pid = 0)
{ $tree = []; if (!empty($list)) { //先修改为以id为下标的列表
$newList = []; foreach ($list as $k => $v) { $newList[$v['id']] = $v;
} //然后开始组装成特殊格式
foreach ($newList as $value) { if ($pid == $value['pid']) {//先取出顶级
$tree[] = &$newList[$value['id']];
} elseif (isset($newList[$value['pid']])) {//再判定非顶级的pid是否存在,如果存在,则再pid所在的数组下面加入一个字段items,来将本身存进去
$newList[$value['pid']]['items'][] = &$newList[$value['id']];
}
}
} return $tree;
}그런 다음 필요한 선택 드롭다운 메뉴를 재귀적으로 생성합니다. 위의 특수 형식으로 인해 재귀가 매우 빠릅니다.
function formatTree($tree)
{ $options = []; if (!empty($tree)) { foreach ($tree as $key => $value) { $options[$value['id']] = $value['name']; if (isset($value['items'])) {//查询是否有子节点
$optionsTmp = $this->formatTree($value['items']); if (!empty($optionsTmp)) { $options = array_merge($options, $optionsTmp);
}
}
}
} return $options;
}위 세 가지는 적은 양의 데이터에 적합하며 어느 것을 사용하든 상관없지만 대량의 데이터에는 효율성이 매우 분명합니다. 4000개의 지역 데이터를 사용한 테스트 결과:
첫 번째 방법(재귀)은 시간이 많이 걸립니다. : 약 8.9441471099854
두 번째 방법(반복) 약 6.7250330448151 소요
세 번째 방법(참조) 시간 소요: 0.028863906860352 왼쪽 및 오른쪽
가자, 이 틈, 세 번째 방법 정말 터무니없습니다. 하지만 이는 한 번에 많은 양의 데이터를 읽을 때만 해당되며, 데이터의 양이 매우 적을 때 그 차이가 가장 효율적일 필요는 없습니다. 지연 로딩과 같은 다른 방법을 통해.
클래스를 캡슐화하면 패딩 등을 추가할 수 있습니다. 자세한 내용은 다음 클래스에서 확인할 수 있습니다.


1 <?php 2 /** 3 * parent_id类型树结构相关 4 * 没必要非要写成静态的方法,静态方法参数太多,所以用实例在构造函数中修改参数更合适 5 * 需要首先将所有数据取出,然后再用此方法重新规划数组,其它的边取边查询数据库的方法不推荐 6 * 经测试第一种方法要快很多,建议使用 7 * @author vishun <nadirvishun@gmail.com> 8 */ 9 10 class Tree 11 { 12 /** 13 * 图标 14 */ 15 public $icon = '└'; 16 /** 17 * 填充 18 */ 19 public $blank = ' '; 20 /** 21 * 默认ID字段名称 22 */ 23 public $idName = 'id'; 24 /** 25 * 默认PID字段名称 26 */ 27 public $pidName = 'pid'; 28 /** 29 * 默认名称字段名称 30 */ 31 public $titleName = 'name'; 32 /** 33 * 默认子元素字段名称 34 */ 35 public $childrenName = 'items'; 36 37 /** 38 * 构造函数,可覆盖默认字段值 39 * @param array $config 40 */ 41 function construct($config = []) 42 { 43 if (!empty($config)) { 44 foreach ($config as $name => $value) { 45 $this->$name = $value; 46 } 47 } 48 } 49 50 /** 51 * 生成下拉菜单可用树列表的方法 52 * 经测试4000条地区数据耗时0.02左右,比另外两种方法快超级多 53 * 流程是先通过引用方法来生成一种特殊树结构,再通过递归来解析这种特殊的结构 54 * @param array $list 55 * @param int $pid 56 * @param int $level 57 * @return array 58 */ 59 public function getTreeOptions($list, $pid = 0, $level = 0) 60 { 61 //先生成特殊规格的树 62 $tree = $this->getTree($list, $pid); 63 //再组装成select需要的形式 64 return $this->formatTree($tree, $level); 65 } 66 67 /** 68 * 通过递归来解析特殊的树结构来组装成下拉菜单所需要的样式 69 * @param array $tree 特殊规格的数组 70 * @param int $level 71 * @return array 72 */ 73 protected function formatTree($tree, $level = 0) 74 { 75 $options = []; 76 if (!empty($tree)) { 77 $blankStr = str_repeat($this->blank, $level) . $this->icon; 78 if ($level == 0) {//第一次无需有图标及空格 79 $blankStr = ''; 80 } 81 foreach ($tree as $key => $value) { 82 $options[$value[$this->idName]] = $blankStr . $value[$this->titleName]; 83 if (isset($value[$this->childrenName])) {//查询是否有子节点 84 $optionsTmp = $this->formatTree($value[$this->childrenName], $level + 1); 85 if (!empty($optionsTmp)) { 86 $options = array_merge($options, $optionsTmp); 87 } 88 } 89 } 90 } 91 return $options; 92 } 93 94 /** 95 * 生成类似下种格式的树结构 96 * 利用了引用&来实现,参照:http://blog.csdn.net/gxdvip/article/details/24434801 97 * [ 98 * 'id'=>1, 99 * 'pid'=>0,100 * 'items'=>[101 * 'id'=>2,102 * 'pid'=>'1'103 * 。。。104 * ]105 * ]106 * @param array $list107 * @param int $pid108 * @return array109 */110 protected function getTree($list, $pid = 0)111 {112 $tree = [];113 if (!empty($list)) {114 //先修改为以id为下标的列表115 $newList = [];116 foreach ($list as $k => $v) {117 $newList[$v[$this->idName]] = $v;118 }119 //然后开始组装成特殊格式120 foreach ($newList as $value) {121 if ($pid == $value[$this->pidName]) {122 $tree[] = &$newList[$value[$this->idName]];123 } elseif (isset($newList[$value[$this->pidName]])) {124 $newList[$value[$this->pidName]][$this->childrenName][] = &$newList[$value[$this->idName]];125 }126 }127 }128 return $tree;129 }130 131 /**132 * 第二种方法,利用出入栈迭代来实现133 * 经测试4000条地区数据耗时6.5s左右,比较慢134 * @param $list135 * @param int $pid136 * @param int $level137 * @return array138 */139 public function getTreeOptions2($list, $pid = 0, $level = 0)140 {141 $tree = [];142 if (!empty($list)) {143 144 //先将数组反转,因为后期出栈时会有限出最上面的145 $list = array_reverse($list);146 //先取出顶级的来压入数组$stack中,并将在$list中的删除掉147 $stack = [];148 foreach ($list as $key => $value) {149 if ($value[$this->pidName] == $pid) {150 array_push($stack, ['data' => $value, 'level' => $level]);//将层级记录下来,方便填充空格151 unset($list[$key]);152 }153 }154 while (count($stack)) {155 //先从栈中取出第一项156 $info = array_pop($stack);157 //查询剩余的$list中pid与其id相等的,也就是查找其子节点158 foreach ($list as $key => $child) {159 if ($child[$this->pidName] == $info['data'][$this->idName]) {160 //如果有子节点则入栈,while循环中会继续查找子节点的下级161 array_push($stack, ['data' => $child, 'level' => $info['level'] + 1]);162 unset($list[$key]);163 }164 }165 //组装成下拉菜单格式166 $blankStr = str_repeat($this->blank, $info['level']) . $this->icon;167 if ($info['level'] == 0) {//第一次无需有图标及空格168 $blankStr = '';169 }170 $tree[$info['data'][$this->idName]] = $blankStr . $info['data'][$this->titleName];171 }172 }173 return $tree;174 }175 176 /**177 * 第三种普通列表转为下拉菜单可用的树列表178 * 经测试4000条地区数据耗时8.7s左右,最慢179 * @param array $list 原数组180 * @param int $pid 起始pid181 * @param int $level 起始层级182 * @return array183 */184 public function getTreeOptions3($list, $pid = 0, $level = 0)185 {186 $options = [];187 if (!empty($list)) {188 $blankStr = str_repeat($this->blank, $level) . $this->icon;189 if ($level == 0) {//第一次无需有图标及空格190 $blankStr = '';191 }192 foreach ($list as $key => $value) {193 if ($value[$this->pidName] == $pid) {194 $options[$value[$this->idName]] = $blankStr . $value[$this->titleName];195 unset($list[$key]);//销毁已查询的,减轻下次递归时查询数量196 $optionsTmp = $this->getTreeOptions3($list, $value[$this->idName], $level + 1);//递归197 if (!empty($optionsTmp)) {198 $options = array_merge($options, $optionsTmp);199 }200 }201 }202 }203 return $options;204 }205 }코드 보기
위 내용을 기록하고, 재인쇄할 경우 출처 주소를 명시해 주세요
위 내용은 세 가지 무한 분류 방식(반복, 재귀, 참조)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7791
7791
 15
15
 1644
1644
 14
14
 1401
1401
 52
52
 1298
1298
 25
25
 1234
1234
 29
29
 C++ 함수의 재귀 구현: 재귀 깊이에 제한이 있나요?
Apr 23, 2024 am 09:30 AM
C++ 함수의 재귀 구현: 재귀 깊이에 제한이 있나요?
Apr 23, 2024 am 09:30 AM
C++ 함수의 재귀 깊이에는 제한이 있습니다. 이 제한을 초과하면 스택 오버플로 오류가 발생합니다. 제한 값은 시스템과 컴파일러에 따라 다르지만 일반적으로 1,000에서 10,000 사이입니다. 솔루션에는 다음이 포함됩니다. 1. 테일 재귀 최적화, 2. 테일 호출, 3. 반복 구현.
 C++ 람다 표현식은 재귀를 지원합니까?
Apr 17, 2024 pm 09:06 PM
C++ 람다 표현식은 재귀를 지원합니까?
Apr 17, 2024 pm 09:06 PM
예, C++ Lambda 표현식은 std::function을 사용하여 재귀를 지원할 수 있습니다. std::function을 사용하여 Lambda 표현식에 대한 참조를 캡처합니다. 캡처된 참조를 사용하면 Lambda 표현식이 자신을 재귀적으로 호출할 수 있습니다.
 Apple Notes에서 블록 따옴표를 사용하는 방법
Oct 12, 2023 pm 11:49 PM
Apple Notes에서 블록 따옴표를 사용하는 방법
Oct 12, 2023 pm 11:49 PM
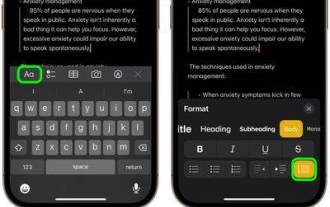
iOS 17 및 macOS Sonoma에서 Apple은 블록 따옴표 및 새로운 모노스타일 스타일을 포함하여 Apple Notes에 대한 새로운 서식 옵션을 추가했습니다. 사용 방법은 다음과 같습니다. Apple Notes의 추가 서식 옵션을 사용하면 이제 메모에 블록 따옴표를 추가할 수 있습니다. 블록 인용 형식을 사용하면 텍스트 왼쪽에 있는 인용 표시줄을 사용하여 글의 섹션을 시각적으로 쉽게 오프셋할 수 있습니다. "Aa" 형식 버튼을 탭/클릭하고 입력하기 전이나 블록 인용으로 변환하려는 줄에 있을 때 블록 인용 옵션을 선택하세요. 이 옵션은 체크리스트를 포함한 모든 텍스트 유형, 스타일 옵션 및 목록에 적용됩니다. 동일한 형식 메뉴에서 새로운 단일 스타일 옵션을 찾을 수 있습니다. 이것은 이전의 "동일 너비"의 개정판입니다.
 C++ 함수의 재귀적 구현: 재귀적 알고리즘과 비재귀적 알고리즘의 비교 분석?
Apr 22, 2024 pm 03:18 PM
C++ 함수의 재귀적 구현: 재귀적 알고리즘과 비재귀적 알고리즘의 비교 분석?
Apr 22, 2024 pm 03:18 PM
재귀 알고리즘은 함수 자체 호출을 통해 구조화된 문제를 해결하지만 간단하고 이해하기 쉽다는 장점이 있지만 효율성이 떨어지고 스택 오버플로가 발생할 수 있다는 단점이 있습니다. 스택 데이터 구조의 장점은 더 효율적이고 스택 오버플로를 방지한다는 것입니다. 단점은 코드가 더 복잡할 수 있다는 것입니다. 재귀적 또는 비재귀적 선택은 문제와 구현의 특정 제약 조건에 따라 달라집니다.
 Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
두 개의 문자열 str_1과 str_2가 주어졌습니다. 목표는 재귀 프로시저를 사용하여 문자열 str1에서 하위 문자열 str2의 발생 횟수를 계산하는 것입니다. 재귀 함수는 정의 내에서 자신을 호출하는 함수입니다. str1이 "Iknowthatyouknowthatiknow"이고 str2가 "know"인 경우 발생 횟수는 -3입니다. 예를 들어 str1="TPisTPareTPamTP", str2="TP"를 입력하면 Countofoccurrencesofasubstringrecursi가 출력됩니다.
 C++ 재귀 고급: 꼬리 재귀 최적화 및 적용 이해
Apr 30, 2024 am 10:45 AM
C++ 재귀 고급: 꼬리 재귀 최적화 및 적용 이해
Apr 30, 2024 am 10:45 AM
TRO(Tail Recursion Optimization)는 특정 재귀 호출의 효율성을 향상시킵니다. 꼬리 재귀 호출을 점프 명령어로 변환하고 컨텍스트 상태를 스택이 아닌 레지스터에 저장하므로 추가 호출을 제거하고 스택에 대한 반환 작업을 제거하고 알고리즘 효율성을 향상시킵니다. TRO를 사용하면 꼬리 재귀 함수(예: 계승 계산)를 최적화할 수 있습니다. 꼬리 재귀 호출을 goto 문으로 대체하면 컴파일러는 goto 점프를 TRO로 변환하고 재귀 알고리즘의 실행을 최적화합니다.
 C++ 함수 재귀에 대한 자세한 설명: 문자열 처리에 재귀 적용
Apr 30, 2024 am 10:30 AM
C++ 함수 재귀에 대한 자세한 설명: 문자열 처리에 재귀 적용
Apr 30, 2024 am 10:30 AM
재귀 함수는 문자열 처리 문제를 해결하기 위해 자신을 반복적으로 호출하는 기술입니다. 무한 재귀를 방지하기 위해서는 종료 조건이 필요합니다. 재귀는 문자열 반전 및 회문 검사와 같은 작업에 널리 사용됩니다.
 참조 유형을 반환하는 C++ 함수의 이점은 무엇입니까?
Apr 20, 2024 pm 09:12 PM
참조 유형을 반환하는 C++ 함수의 이점은 무엇입니까?
Apr 20, 2024 pm 09:12 PM
C++에서 참조 유형을 반환하는 함수의 이점은 다음과 같습니다. 성능 개선: 참조로 전달하면 객체 복사가 방지되므로 메모리와 시간이 절약됩니다. 직접 수정: 호출자는 반환된 참조 객체를 다시 할당하지 않고 직접 수정할 수 있습니다. 코드 단순성: 참조로 전달하면 코드가 단순화되고 추가 할당 작업이 필요하지 않습니다.




