JAVA 정렬 힙 정렬
아래 편집기는 비교 정렬 및 힙 정렬에 대한 진부한 표현을 제공합니다. 에디터가 꽤 좋다고 생각해서 지금 공유해서 참고용으로 올려보겠습니다.
힙 정렬에는 완전한 이진 트리 지식이 필요합니다. 시퀀스를 {10, 2, 11, 8, 7}로 정렬하려면 아래 그림과 같이 완전한 이진 트리로 간주하세요.
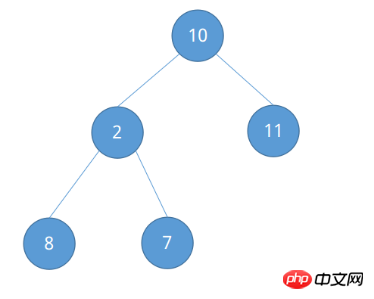
힙은 큰 루트 힙과 작은 루트 힙으로 나뉩니다. 큰 루트 힙은 각 루트 노드가 하위 노드(L(i) >= L(2i) && L(i) > = L(2i + 1)), 작은 루트 힙은 각 루트 노드가 하위 노드(L(i)
이 기사에서는 대규모 루트 힙 구성을 예로 들어 설명합니다. .
힙 정렬의 첫 번째 단계 - 초기 힙 구축. 초기 힙을 구축하는 방법은 무엇입니까? 정의에 따르면 핵심 포인트는 각 루트 노드에 있습니다. 위에서 언급한 정렬 대상 시퀀스의 완전한 이진 트리를 관찰하면 노드 2와 노드 10에 주의가 필요한 노드인 자식 노드가 있음을 찾는 것은 어렵지 않습니다.
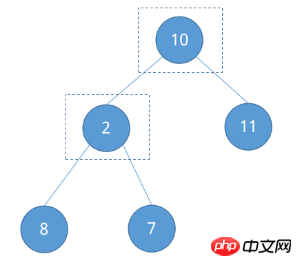
노드 2를 찾는 방법은 무엇인가요? 리프 노드, 즉 마지막 노드의 부모 노드임을 알 수 있는데, 완전 이진 트리의 속성에 따르면 루트 노드를 제외한 모든 노드의 부모 노드 수는 ⌊n/2⌋이다. n = 5라고 가정하면 노드 2의 개수가 ⌊5 / 2⌋ = ②라는 것을 쉽게 알 수 있습니다. 왼쪽과 오른쪽 자식 노드의 크기를 비교하여 조정합니다.
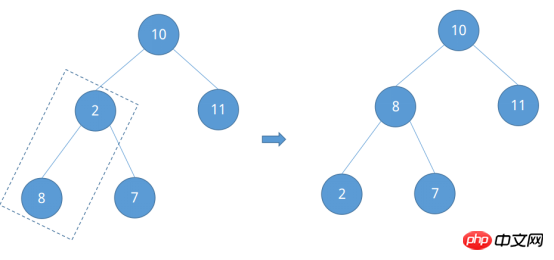
드디어 루트 노드 10이 남았습니다. 노드 2의 개수는 ②, ② - 1 = ①인 것으로 알려져 있는데, 이는 루트 노드 10의 개수를 얻게 된다는 의미입니다. 왼쪽과 오른쪽 자식 노드의 크기를 비교하여 조정합니다.
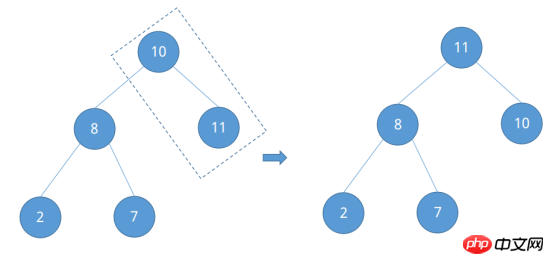
조정이 완료되면 "큰 루트 힙"이 형성된 것을 확인할 수 있습니다. 예제에서 정렬할 열은 비교적 간단하며, 관찰하기 위해 더 복잡한 정렬할 열을 제공합니다. 큰 루트 힙을 구축하는 과정입니다. {53, 17, 78, 09, 45, 65, 87, 32}로 정렬되는 시퀀스의 경우 이를 완전한 이진 트리로 처리합니다.
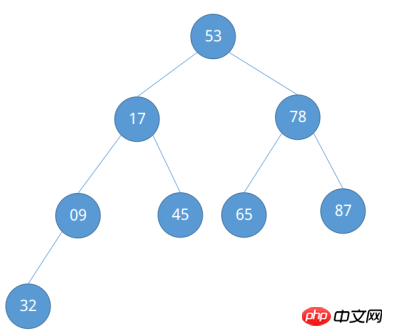
마찬가지로 주의해야 할 노드를 살펴보겠습니다.
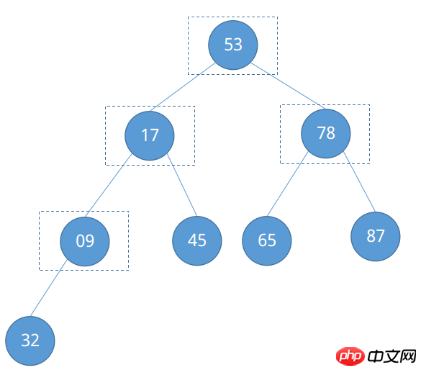
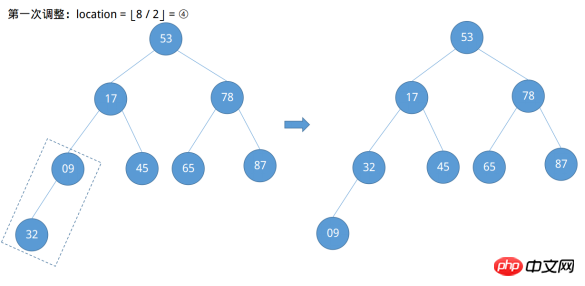
첫 번째 예에 따르면 노드 09의 번호는 ⌊8 / 2⌋ = ④로, 노드 78의 번호는 ④ - 1 = ③... 등으로 쉽게 찾을 수 있습니다. 즉, 조정해야 할 노드 위치는 ⌊n / 2⌋부터 루트 노드 ①이 끝날 때까지 (⌊n / 2) 감소합니다. ⌋ ~ 1). 지금 조정을 시작하세요. ㅋㅋㅋ 추가 하향 조정이 필요합니다.
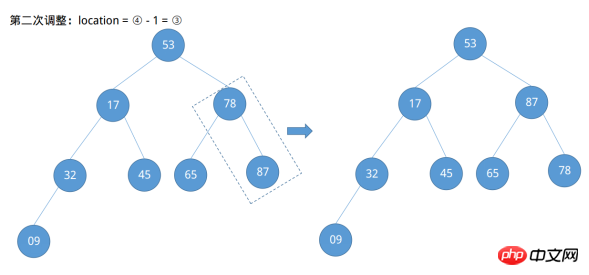
루트 노드와 마지막 노드를 호출한 후 정렬할 열의 최대값이 배열의 마지막 위치인 {..., 87}에 배치된 것을 확인할 수 있습니다. 이때 첫 번째 정렬은 다음과 같습니다. 완료되었으나 이 첫 번째 정렬은 아직 끝나지 않았습니다. 노드 87을 제외하고 다른 노드는 큰 루트 힙의 조건을 충족하지 않으므로 나머지 노드는 큰 루트 힙이 되도록 조정해야 합니다. 정렬 프로세스는 더 이상 제공되지 않습니다. Java 및 Python3의 코드 구현은 다음과 같습니다.
Java
package com.algorithm.sort.heap;
import java.util.Arrays;
/**
* 堆排序
* Created by yulinfeng on 6/20/17.
*/
public class Heap {
public static void main(String[] args) {
int[] nums = {53, 17, 78, 09, 45, 65, 87, 32};
nums = heapSort(nums);
System.out.println(Arrays.toString(nums));
}
/**
* 堆排序
* @param nums 待排序数组序列
* @return 排好序的数组序列
*/
private static int[] heapSort(int[] nums) {
for (int i = nums.length / 2 - 1; i >= 0; i--) {
heapAdjust(nums, i, nums.length);
}
for (int i = nums.length - 1; i > 0; i--) {
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
heapAdjust(nums, 0, i);
}
return nums;
}
/**
* 调整堆
*
* @param nums 待排序序列
* @param parent 待调整根节点
* @param length 数组序列长度
*/
private static void heapAdjust(int[] nums, int parent, int length) {
int temp = nums[parent];
int childIndex = 2 * parent + 1; //完全二叉树节点i从编号1开始的左子节点位置在2i,此处数组下标从0开始,即左子节点所在数组索引位置为:2i + 1
while (childIndex < length) {
if (childIndex + 1 < length && nums[childIndex] < nums[childIndex + 1]) {
childIndex++; //节点有右子节点,且右子节点大于左子节点,则选取右子节点
}
if (temp > nums[childIndex]) {
break; //如果选中节点大于其子节点,直接返回
}
nums[parent] = nums[childIndex];
parent = childIndex;
childIndex = 2 * parent + 1; //继续向下调整
}
nums[parent] = temp;
}
}Python3
#堆排序
def heap_sort(nums):
for i in range(int(len(nums) / 2 - 1), -1, -1):
heap_adjust(nums, i, len(nums))
for i in range(len(nums) - 1, -1, -1):
temp = nums[i]
nums[i] = nums[0]
nums[0] = temp
heap_adjust(nums, 0, i)
return nums
#调整堆
def heap_adjust(nums, parent, length):
temp = nums[parent]
childIndex = 2 * parent + 1
while childIndex < length:
if childIndex + 1 < length and nums[childIndex] < nums[childIndex + 1]:
childIndex += 1
if temp > nums[childIndex]:
break
nums[parent] = nums[childIndex]
parent = childIndex
childIndex = 2 * parent + 1
nums[parent] = temp
nums = [53, 17, 78, 09, 45, 65, 87, 32]
nums = heap_sort(nums)
print(nums)위의 진부한 비교정렬과 힙정렬은 모두 에디터가 공유해드린 내용이니 참고가 되셨으면 좋겠습니다. , 모두가 Script House를 지지해 주시길 바랍니다.
위 내용은 JAVA 정렬 힙 정렬의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7706
7706
 15
15
 1640
1640
 14
14
 1394
1394
 52
52
 1288
1288
 25
25
 1231
1231
 29
29
 Java의 스미스 번호
Aug 30, 2024 pm 04:28 PM
Java의 스미스 번호
Aug 30, 2024 pm 04:28 PM
Java의 Smith Number 가이드. 여기서는 정의, Java에서 스미스 번호를 확인하는 방법에 대해 논의합니다. 코드 구현의 예.
 Java Spring 인터뷰 질문
Aug 30, 2024 pm 04:29 PM
Java Spring 인터뷰 질문
Aug 30, 2024 pm 04:29 PM
이 기사에서는 가장 많이 묻는 Java Spring 면접 질문과 자세한 답변을 보관했습니다. 그래야 면접에 합격할 수 있습니다.
 Java 8 Stream foreach에서 나누거나 돌아 오시겠습니까?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream foreach에서 나누거나 돌아 오시겠습니까?
Feb 07, 2025 pm 12:09 PM
Java 8은 스트림 API를 소개하여 데이터 컬렉션을 처리하는 강력하고 표현적인 방법을 제공합니다. 그러나 스트림을 사용할 때 일반적인 질문은 다음과 같은 것입니다. 기존 루프는 조기 중단 또는 반환을 허용하지만 스트림의 Foreach 메소드는이 방법을 직접 지원하지 않습니다. 이 기사는 이유를 설명하고 스트림 처리 시스템에서 조기 종료를 구현하기위한 대체 방법을 탐색합니다. 추가 읽기 : Java Stream API 개선 스트림 foreach를 이해하십시오 Foreach 메소드는 스트림의 각 요소에서 하나의 작업을 수행하는 터미널 작동입니다. 디자인 의도입니다
 Java의 날짜까지의 타임스탬프
Aug 30, 2024 pm 04:28 PM
Java의 날짜까지의 타임스탬프
Aug 30, 2024 pm 04:28 PM
Java의 TimeStamp to Date 안내. 여기서는 소개와 예제와 함께 Java에서 타임스탬프를 날짜로 변환하는 방법에 대해서도 설명합니다.
 캡슐의 양을 찾기위한 Java 프로그램
Feb 07, 2025 am 11:37 AM
캡슐의 양을 찾기위한 Java 프로그램
Feb 07, 2025 am 11:37 AM
캡슐은 3 차원 기하학적 그림이며, 양쪽 끝에 실린더와 반구로 구성됩니다. 캡슐의 부피는 실린더의 부피와 양쪽 끝에 반구의 부피를 첨가하여 계산할 수 있습니다. 이 튜토리얼은 다른 방법을 사용하여 Java에서 주어진 캡슐의 부피를 계산하는 방법에 대해 논의합니다. 캡슐 볼륨 공식 캡슐 볼륨에 대한 공식은 다음과 같습니다. 캡슐 부피 = 원통형 볼륨 2 반구 볼륨 안에, R : 반구의 반경. H : 실린더의 높이 (반구 제외). 예 1 입력하다 반경 = 5 단위 높이 = 10 단위 산출 볼륨 = 1570.8 입방 단위 설명하다 공식을 사용하여 볼륨 계산 : 부피 = π × r2 × h (4
 PHP vs. Python : 차이점 이해
Apr 11, 2025 am 12:15 AM
PHP vs. Python : 차이점 이해
Apr 11, 2025 am 12:15 AM
PHP와 Python은 각각 고유 한 장점이 있으며 선택은 프로젝트 요구 사항을 기반으로해야합니다. 1.PHP는 간단한 구문과 높은 실행 효율로 웹 개발에 적합합니다. 2. Python은 간결한 구문 및 풍부한 라이브러리를 갖춘 데이터 과학 및 기계 학습에 적합합니다.
 PHP : 웹 개발의 핵심 언어
Apr 13, 2025 am 12:08 AM
PHP : 웹 개발의 핵심 언어
Apr 13, 2025 am 12:08 AM
PHP는 서버 측에서 널리 사용되는 스크립팅 언어이며 특히 웹 개발에 적합합니다. 1.PHP는 HTML을 포함하고 HTTP 요청 및 응답을 처리 할 수 있으며 다양한 데이터베이스를 지원할 수 있습니다. 2.PHP는 강력한 커뮤니티 지원 및 오픈 소스 리소스를 통해 동적 웹 컨텐츠, 프로세스 양식 데이터, 액세스 데이터베이스 등을 생성하는 데 사용됩니다. 3. PHP는 해석 된 언어이며, 실행 프로세스에는 어휘 분석, 문법 분석, 편집 및 실행이 포함됩니다. 4. PHP는 사용자 등록 시스템과 같은 고급 응용 프로그램을 위해 MySQL과 결합 할 수 있습니다. 5. PHP를 디버깅 할 때 error_reporting () 및 var_dump ()와 같은 함수를 사용할 수 있습니다. 6. 캐싱 메커니즘을 사용하여 PHP 코드를 최적화하고 데이터베이스 쿼리를 최적화하며 내장 기능을 사용하십시오. 7
 미래를 창조하세요: 완전 초보자를 위한 Java 프로그래밍
Oct 13, 2024 pm 01:32 PM
미래를 창조하세요: 완전 초보자를 위한 Java 프로그래밍
Oct 13, 2024 pm 01:32 PM
Java는 초보자와 숙련된 개발자 모두가 배울 수 있는 인기 있는 프로그래밍 언어입니다. 이 튜토리얼은 기본 개념부터 시작하여 고급 주제를 통해 진행됩니다. Java Development Kit를 설치한 후 간단한 "Hello, World!" 프로그램을 작성하여 프로그래밍을 연습할 수 있습니다. 코드를 이해한 후 명령 프롬프트를 사용하여 프로그램을 컴파일하고 실행하면 "Hello, World!"가 콘솔에 출력됩니다. Java를 배우면 프로그래밍 여정이 시작되고, 숙달이 깊어짐에 따라 더 복잡한 애플리케이션을 만들 수 있습니다.




