이 글은 주로 자바스크립트에서 일반적으로 사용되는 기본 정렬 알고리즘을 자세히 소개합니다. 관심 있는 친구들이 참고할 수 있습니다.
참고: 대부분의 내용은 인터넷에서 복사되었으며 코드는 직접 작성했습니다. 독창성이 아닌 과거와 새로운 지식에 대한 검토 일뿐입니다.
1. 버블 정렬
(1) 알고리즘 설명
버블 정렬은 간단한 정렬 알고리즘입니다. 정렬할 순서를 반복적으로 살펴보며 한 번에 두 개의 요소를 비교하고 순서가 잘못된 경우 교체합니다. 더 이상 교환이 필요하지 않을 때까지 어레이 방문 작업이 반복됩니다. 이는 어레이가 정렬되었음을 의미합니다. 이 알고리즘의 이름은 작은 요소가 스와핑을 통해 배열의 맨 위로 천천히 "부동"된다는 사실에서 유래되었습니다.
(2) 알고리즘 설명 및 구현
특정 알고리즘은 다음과 같이 설명됩니다.
<1>. 첫 번째 요소가 두 번째 요소보다 크면 두 요소를 <2>로 교체합니다. 시작 부분의 첫 번째 쌍부터 끝 부분의 마지막 쌍까지 동일한 작업을 수행합니다. 가장 큰 숫자인 <3>이어야 합니다. 마지막 <4>를 제외한 모든 요소에 대해 위의 단계를 반복합니다.
JavaScript 코드 구현:

향상된 버블 정렬: 각 정렬 패스에서 마지막으로 교환된 위치를 기록하도록 아이콘 변수 pos를 설정합니다. pos 위치 이후의 레코드가 제자리에서 교환되었으므로 다음 정렬 과정에서는 pos 위치만 스캔하면 됩니다.
개선된 알고리즘은 다음과 같습니다.

기존 버블 정렬에서는 각 정렬 작업에서 하나의 최대값 또는 최소값만 찾을 수 있습니다. 각 정렬 단계에서 정방향 및 역방향 버블을 사용하여 두 개의 최종 값을 얻을 수 있습니다. (최대 및 최소)를 한 번에 수행하므로 정렬 패스 수가 거의 절반으로 줄어듭니다.
개선된 알고리즘은 다음과 같습니다.

세 가지 알고리즘의 실행 시간은
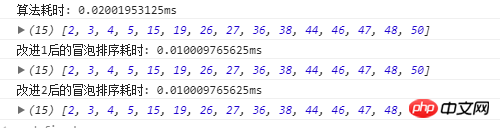
실행 결과를 보면 시간 복잡도가 낮아지고 소비 시간이 짧아지는 것을 확인할 수 있습니다. 직접 시도해 볼 수도 있습니다. 실행할 때 세 가지 알고리즘을 하나의 파일에 작성하는 것이 가장 좋습니다. 그렇지 않으면 브라우저 및 기타 이유로 오류가 발생합니다.
버블 정렬의 동적 다이어그램 데모:
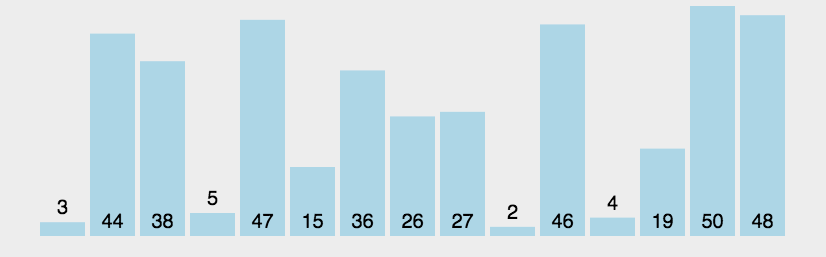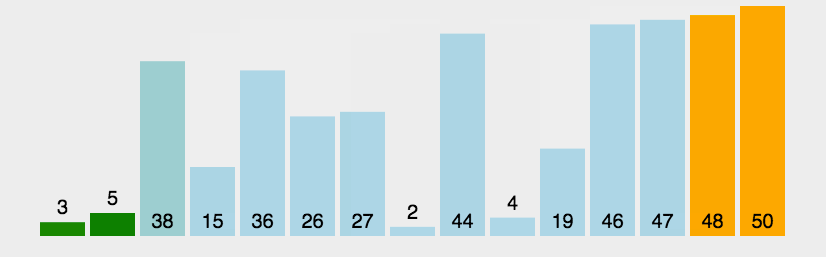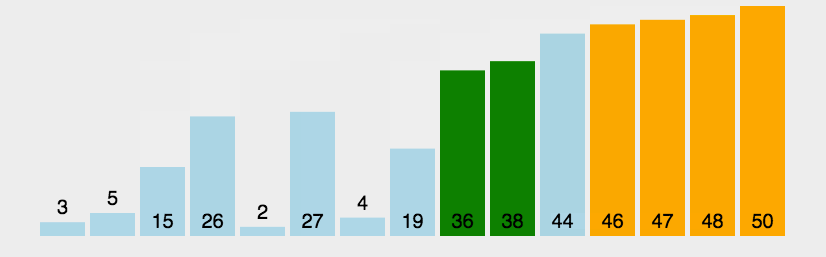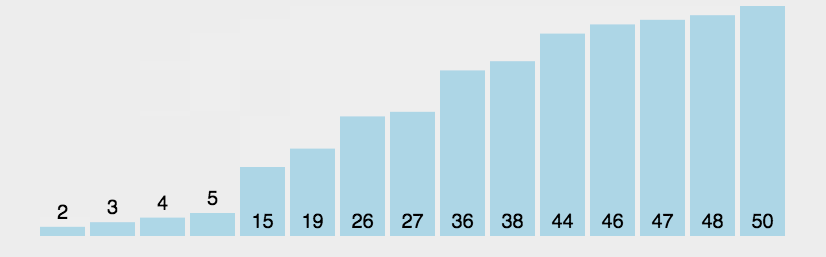
(3) 알고리즘 분석
최상의 사례: T(n) = O(n)
입력 데이터가 이미 양수 순서인 경우
최악의 사례: T (n) = O(n2)
입력 데이터가 역순일 때
평균 상황: T(n) = O(n2)
2. Selection Sort
최고의 성능을 보이는 안정적인 정렬 중 하나 알고리즘은 어떤 데이터를 입력하더라도 시간복잡도는 O(n²)이기 때문에, 데이터 크기가 작을수록 좋습니다. 유일한 장점은 추가 메모리 공간을 차지하지 않는다는 것입니다. 이론적으로 말하면, 선택 정렬은 대부분의 사람들이 정렬할 때 생각하는 가장 일반적인 정렬 방법일 수도 있습니다.
(1) 알고리즘 소개
Selection-sort는 간단하고 직관적인 정렬 알고리즘입니다. 작동 방식: 먼저 정렬되지 않은 시퀀스에서 가장 작은(큰) 요소를 찾아 정렬된 시퀀스의 시작 위치에 저장한 다음, 정렬되지 않은 나머지 요소에서 계속해서 가장 작은(큰) 요소를 찾아 넣습니다. 정렬된 순서로 끝납니다. 모든 요소가 정렬될 때까지 계속됩니다.
(2) 알고리즘 설명 및 구현
n 레코드의 직접 선택 정렬은 n-1 직접 선택 정렬 패스를 통해 정렬된 결과를 얻을 수 있습니다. 구체적인 알고리즘은 다음과 같습니다:
. 초기 상태: 정렬되지 않은 영역은 R[1..n]이고, 정렬된 영역은 비어 있습니다(i=1). ,2,3 ...n-1) 처음에는 현재 정렬된 영역과 정렬되지 않은 영역이 각각 R[1..i-1] 및 R(i..n)입니다. 이러한 정렬 연산은 현재 무질서한 영역에서 키가 가장 작은 레코드 R[k]를 선택하여 무질서한 영역의 첫 번째 레코드 R과 교환함으로써 R[1..i]와 R[i+1 .. n) 각각 레코드 수가 1만큼 증가한 새로운 정렬된 영역과 1만큼 감소된 새로운 정렬되지 않은 영역이 됩니다.n-1 패스가 끝나고 배열이 정렬됩니다.
Javascript 코드 구현:
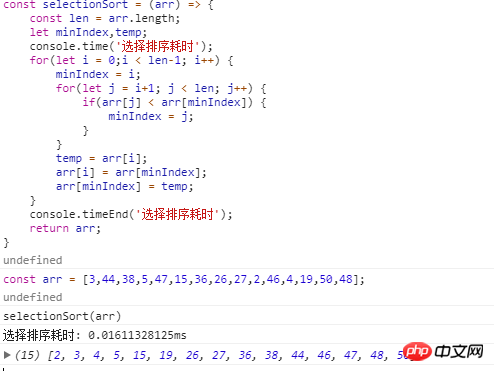
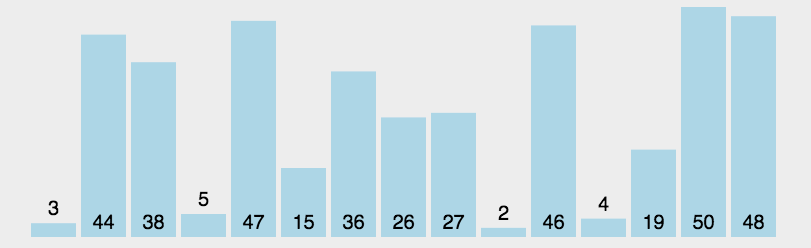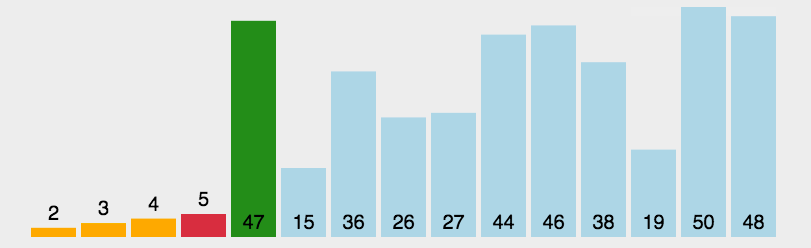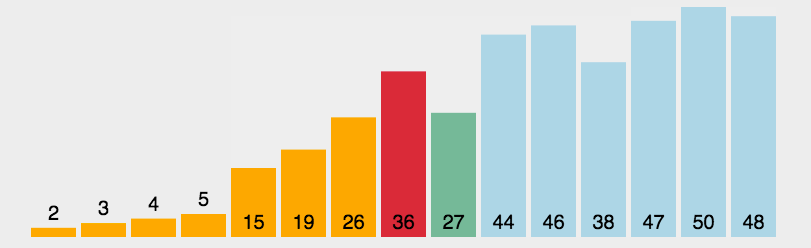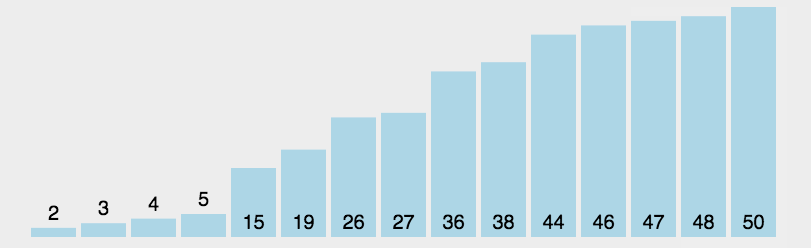
(3) 알고리즘 분석
최상의 경우: T(n) = O(n2) 최악의 경우: T(n) = O(n2) 평균 경우: T( n) = O(n2)
위 내용은 JavaScript에서 일반적으로 사용되는 기본 정렬 알고리즘의 분석 예의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!