물리학에서 이중 스프링 질량 에너지 시스템을 해결하기 위한 Python 코드 예제

이 글은 물리학에서 이중 스프링 질량 에너지 시스템을 해결하기 위해 Python을 사용하는 방법에 대한 관련 정보를 주로 소개합니다. 이 글은 모든 사람의 학습이나 작업에 대한 특정 참고 학습 가치를 제공합니다. 친구가 필요하고, 편집자를 따라가서 함께 배워보세요.

머리말

이 글은 물리학에서 이중 스프링 질량 에너지 시스템을 해결하기 위해 Python을 사용하는 것과 관련된 내용을 주로 소개하며, 참고 및 연구를 위해 공유합니다. 아래에서는 많은 말을 하지 않겠습니다. , 세부 사항을 살펴 보겠습니다.

물리적 모델은 다음과 같습니다:

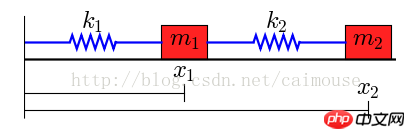
이 시스템에는 두 개의 물체가 있으며, 질량은 각각 m1과 m2이고 두 개의 스프링으로 서로 연결되어 있으며 망원경 시스템은 k1과 k2이며 왼쪽 끝입니다. 결정된. 외력이 없다고 가정하면 두 스프링의 길이는 L1과 L2입니다.

두 물체에는 중력이 있으므로 평면에 마찰이 생기고 마찰계수는 각각 b1과 b2가 됩니다. 따라서 다음과 같이 미분방정식을 작성할 수 있습니다.

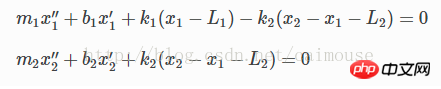
이것은 2차 미분방정식입니다. 이를 Python을 사용하여 풀려면 1차 미분방정식으로 변환해야 합니다. 따라서 다음 두 가지 변수가 도입됩니다.

이 두 변수는 이동 속도와 동일합니다. 연산을 통해 이렇게 바꿀 수 있습니다:

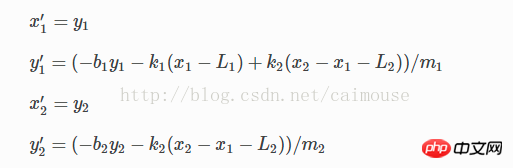
이때 선형방정식을 벡터배열로 바꿀 수 있고, 파이썬을 이용해 정의할 수 있습니다.

코드는 다음과 같습니다.

# Use ODEINT to solve the differential equations defined by the vector field 
from scipy.integrate import odeint 
 
def vectorfield(w, t, p): 
 """ 
 Defines the differential equations for the coupled spring-mass system. 
 
 Arguments: 
  w : vector of the state variables: 
     w = [x1,y1,x2,y2] 
  t : time 
  p : vector of the parameters: 
     p = [m1,m2,k1,k2,L1,L2,b1,b2] 
 """ 
 x1, y1, x2, y2 = w 
 m1, m2, k1, k2, L1, L2, b1, b2 = p 
 
 # Create f = (x1',y1',x2',y2'): 
 f = [y1, 
   (-b1 * y1 - k1 * (x1 - L1) + k2 * (x2 - x1 - L2)) / m1, 
   y2, 
   (-b2 * y2 - k2 * (x2 - x1 - L2)) / m2] 
 return f 
 
# Parameter values 
# Masses: 
m1 = 1.0 
m2 = 1.5 
# Spring constants 
k1 = 8.0 
k2 = 40.0 
# Natural lengths 
L1 = 0.5 
L2 = 1.0 
# Friction coefficients 
b1 = 0.8 
b2 = 0.5 
 
# Initial conditions 
# x1 and x2 are the initial displacements; y1 and y2 are the initial velocities 
x1 = 0.5 
y1 = 0.0 
x2 = 2.25 
y2 = 0.0 
 
# ODE solver parameters 
abserr = 1.0e-8 
relerr = 1.0e-6 
stoptime = 10.0 
numpoints = 250 
 
# Create the time samples for the output of the ODE solver. 
# I use a large number of points, only because I want to make 
# a plot of the solution that looks nice. 
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)] 
 
# Pack up the parameters and initial conditions: 
p = [m1, m2, k1, k2, L1, L2, b1, b2] 
w0 = [x1, y1, x2, y2] 
 
# Call the ODE solver. 
wsol = odeint(vectorfield, w0, t, args=(p,), 
    atol=abserr, rtol=relerr) 
 
with open('two_springs.dat', 'w') as f: 
 # Print & save the solution. 
 for t1, w1 in zip(t, wsol):   
  out = '{0} {1} {2} {3} {4}\n'.format(t1, w1[0], w1[1], w1[2], w1[3]); 
  print(out) 
  f.write(out);

여기에 결과를 출력합니다. two_springs.dat 파일로 가서 데이터를 그림으로 표시하는 프로그램을 작성하면 코드는 다음과 같습니다.

# Plot the solution that was generated 
 
from numpy import loadtxt 
from pylab import figure, plot, xlabel, grid, hold, legend, title, savefig 
from matplotlib.font_manager import FontProperties 
 
t, x1, xy, x2, y2 = loadtxt('two_springs.dat', unpack=True) 
 
figure(1, figsize=(6, 4.5)) 
 
xlabel('t') 
grid(True) 
lw = 1 
 
plot(t, x1, 'b', linewidth=lw) 
plot(t, x2, 'g', linewidth=lw) 
 
legend((r'$x_1$', r'$x_2$'), prop=FontProperties(size=16)) 
title('Mass Displacements for the\nCoupled Spring-Mass System') 
savefig('two_springs.png', dpi=100)

마지막으로, 다음과 같이 출력된 png 그림을 확인해 보겠습니다.

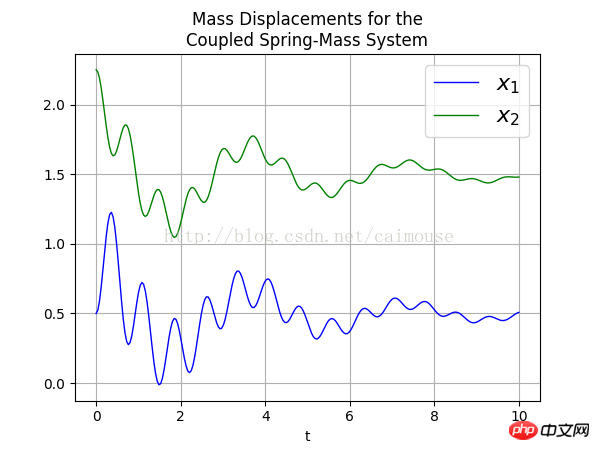
요약

위 내용은 물리학에서 이중 스프링 질량 에너지 시스템을 해결하기 위한 Python 코드 예제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!