Java에서 최단 경로 알고리즘을 위한 Dijkstra 알고리즘 구현

이 글에서는 주로 Java에서 최단 경로 알고리즘을 구현한 Dijkstra 알고리즘을 소개합니다. Dijkstra 알고리즘은 단일 시작 전체 경로 알고리즘입니다.

머리말

Dijkstra의 알고리즘은 잘 알려진 최단 경로 알고리즘이며 단일 시작 전체 경로 알고리즘입니다. 이 알고리즘은 '탐욕 알고리즘'의 성공적인 사례라고 불린다. 이 기사에서는 가장 널리 사용되는 언어로 이 훌륭한 알고리즘을 소개하고 Java 구현 코드를 제공하려고 합니다.

1. 지식 준비:

1. 그래프를 나타내는 데이터 구조

이 알고리즘에서는 저자가 인접 행렬을 사용합니다.

그래프의 인접 행렬 저장 방법은 두 개의 배열을 사용하여 그래프를 표현하는 것입니다. 1차원 배열은 그래프에 정점 정보를 저장하고, 2차원 배열(인접 행렬)은 그래프에 모서리 또는 호 정보를 저장합니다.

그래프 G에 n개의 정점이 있다고 가정하면 인접 행렬은 다음과 같이 정의되는 n*n 정사각형 행렬입니다.

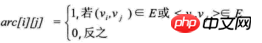
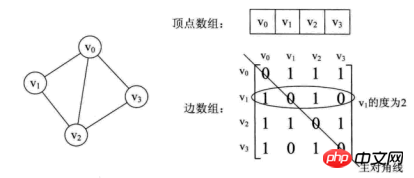
위에서 볼 수 있듯이 무향 그래프의 가장자리 배열은 대칭 행렬입니다. 소위 대칭 행렬은 n차 행렬의 요소가 aij = aji를 충족한다는 것을 의미합니다. 즉, 행렬의 왼쪽 위 모서리부터 오른쪽 아래 모서리까지의 주대각선이 축이고, 오른쪽 위 모서리에 있는 요소와 왼쪽 아래 모서리에 해당하는 요소가 모두 동일합니다.

이 매트릭스를 통해 사진 속 정보를 쉽게 알 수 있습니다.

(1) 두 정점에 가장자리가 있는지 없는지 확인하는 것은 매우 쉽습니다.

(2) 특정 정점의 차수를 아는 것은 실제로 정점 vi가 i번째 행에 있거나 또는 (i번째 열) 인접 행렬의 요소인 out-degree와 out-degree의 합, 정점 vi의 in-degree는 1이며, 이는 정확히 i번째 열에 있는 숫자의 합입니다. 정점 vi의 진출 차수는 2이며, 이는 i번째 행에 있는 숫자의 합입니다.

유향 그래프의 정의도 비슷하므로 자세한 내용은 다루지 않겠습니다.

2. 단일 시작점 전체 경로

소위 단일 시작점 전체 경로는 시작점에서 시작하여 그래프의 모든 노드까지의 최단 경로를 말합니다.

3. 그래프 이론의 기본 지식(관련 정보는 독자가 직접 찾아야 함)

4. 보완 완화 조건

스칼라 d1, d2,...,dN이 dj< =di + aij, (i, j)는 A,

에 속하며 P는 i1이 시작점이고 ik가 끝점인 도로입니다.

dj = di + aij이면 모든 측면에 적용됩니다(i, j) P의 다음 P i1에서 ik까지의 최단 경로입니다. 그 중에서 위의 두 방정식을 만족하는 최단경로 문제의 상보적 완화조건을 호칭한다.

2. 알고리즘 아이디어

1. G = (V, E)를 가중 무방향 그래프로 둡니다. G에 두 개의 인접한 노드가 있는 경우 i와 j입니다. aij(여기서부터 나중에 아래 첨자로 표현됨)는 노드 i에서 노드 j까지의 가중치이며, 이 알고리즘에서는 거리로 이해될 수 있습니다. 각 노드에는 시작점에서 특정 경로까지의 거리를 나타내는 di(노드 라벨) 값이 있습니다. 2. 알고리즘에는 처음에 방문하지 않은 노드 목록을 저장하는 데 사용되는 배열 V가 있으며, 이를 일시적으로 후보 목록이라고 합니다. 시작 노드로 노드 1을 선택합니다. 처음에는 노드 1의 경우 d1=0이고 다른 노드의 경우 di=무한대이며 V는 모든 노드입니다. 조건을 초기화한 후 반복 알고리즘을 시작하고 V가 공집합이 되면 중지합니다. 구체적인 반복 단계는 다음과 같습니다.

후보 목록에서 d 값이 가장 작은 노드 di를 제거합니다. (이 예에서 V의 데이터 구조는 우선순위 큐를 사용하여 최소값 dequeue를 구현합니다. 이전 기사에서 소개한 Fibonacci 쌍을 사용하는 것이 가장 좋으며 성능이 크게 향상됩니다.) V가 제거된 노드를 제외하고 이 노드에서 시작하는 모든 간선에 대해 (i, j)는 A에 속합니다. dj > di + aij(완화 조건 위반)이면

dj = di + aij , ( j가 V에서 제거된 경우 이는 최소 거리가 계산되었으며 이 계산에 참여하지 않는다는 의미입니다.)

알고리즘의 운영 엔지니어링에서 노드의 d 값이 단조롭게 증가하지 않는 것을 볼 수 있습니다

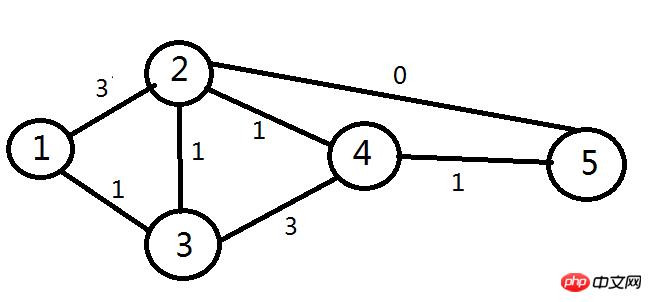
구체적인 알고리즘 다이어그램은 다음과 같습니다

　

3. Java 코드 구현

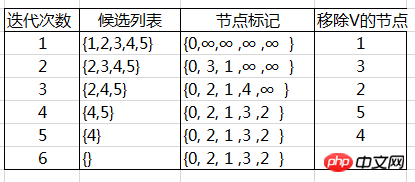
public class Vertex implements Comparable<Vertex>{

  /**
   * 节点名称(A,B,C,D)
   */
  private String name;
  
  /**
   * 最短路径长度
   */
  private int path;
  
  /**
   * 节点是否已经出列(是否已经处理完毕)
   */
  private boolean isMarked;
  
  public Vertex(String name){
    this.name = name;
    this.path = Integer.MAX_VALUE; //初始设置为无穷大
    this.setMarked(false);
  }
  
  public Vertex(String name, int path){
    this.name = name;
    this.path = path;
    this.setMarked(false);
  }
  
  @Override
  public int compareTo(Vertex o) {
    return o.path > path?-1:1;
  }
}

public class Graph {

  /*
   * 顶点
   */
  private List<Vertex> vertexs;

  /*
   * 边
   */
  private int[][] edges;

  /*
   * 没有访问的顶点
   */
  private Queue<Vertex> unVisited;

  public Graph(List<Vertex> vertexs, int[][] edges) {
    this.vertexs = vertexs;
    this.edges = edges;
    initUnVisited();
  }
  
  /*
   * 搜索各顶点最短路径
   */
  public void search(){
    while(!unVisited.isEmpty()){
      Vertex vertex = unVisited.element();
      //顶点已经计算出最短路径，设置为"已访问"
     　　vertex.setMarked(true);  
      //获取所有"未访问"的邻居
      　　List<Vertex> neighbors = getNeighbors(vertex);  
      //更新邻居的最短路径
      updatesDistance(vertex, neighbors);    
      pop();
    }
    System.out.println("search over");
  }
  
  /*
   * 更新所有邻居的最短路径
   */
  private void updatesDistance(Vertex vertex, List<Vertex> neighbors){
    for(Vertex neighbor: neighbors){
      updateDistance(vertex, neighbor);
    }
  }
  
  /*
   * 更新邻居的最短路径
   */
  private void updateDistance(Vertex vertex, Vertex neighbor){
    int distance = getDistance(vertex, neighbor) + vertex.getPath();
    if(distance < neighbor.getPath()){
      neighbor.setPath(distance);
    }
  }

  /*
   * 初始化未访问顶点集合
   */
  private void initUnVisited() {
    unVisited = new PriorityQueue<Vertex>();
    for (Vertex v : vertexs) {
      unVisited.add(v);
    }
  }

  /*
   * 从未访问顶点集合中删除已找到最短路径的节点
   */
  private void pop() {
    unVisited.poll();
  }

  /*
   * 获取顶点到目标顶点的距离
   */
  private int getDistance(Vertex source, Vertex destination) {
    int sourceIndex = vertexs.indexOf(source);
    int destIndex = vertexs.indexOf(destination);
    return edges[sourceIndex][destIndex];
  }

  /*
   * 获取顶点所有(未访问的)邻居
   */
  private List<Vertex> getNeighbors(Vertex v) {
    List<Vertex> neighbors = new ArrayList<Vertex>();
    int position = vertexs.indexOf(v);
    Vertex neighbor = null;
    int distance;
    for (int i = 0; i < vertexs.size(); i++) {
      if (i == position) {
        //顶点本身，跳过
        continue;
      }
      distance = edges[position][i];  //到所有顶点的距离
      if (distance < Integer.MAX_VALUE) {
        //是邻居(有路径可达)
        neighbor = getVertex(i);
        if (!neighbor.isMarked()) {
          //如果邻居没有访问过，则加入list;
          neighbors.add(neighbor);
        }
      }
    }
    return neighbors;
  }

  /*
   * 根据顶点位置获取顶点
   */
  private Vertex getVertex(int index) {
    return vertexs.get(index);
  }

  /*
   * 打印图
   */
  public void printGraph() {
    int verNums = vertexs.size();
    for (int row = 0; row < verNums; row++) {
      for (int col = 0; col < verNums; col++) {
        if(Integer.MAX_VALUE == edges[row][col]){
          System.out.print("X");
          System.out.print(" ");
          continue;
        }
        System.out.print(edges[row][col]);
        System.out.print(" ");
      }
      System.out.println();
    }
  }
}

public class Test {

  public static void main(String[] args){
    List<Vertex> vertexs = new ArrayList<Vertex>();
    Vertex a = new Vertex("A", 0);
    Vertex b = new Vertex("B");
    Vertex c = new Vertex("C");
    Vertex d = new Vertex("D");
    Vertex e = new Vertex("E");
    Vertex f = new Vertex("F");
    vertexs.add(a);
    vertexs.add(b);
    vertexs.add(c);
    vertexs.add(d);
    vertexs.add(e);
    vertexs.add(f);
    int[][] edges = {
        {Integer.MAX_VALUE,6,3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {6,Integer.MAX_VALUE,2,5,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {3,2,Integer.MAX_VALUE,3,4,Integer.MAX_VALUE},
        {Integer.MAX_VALUE,5,3,Integer.MAX_VALUE,5,3},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,4,5,Integer.MAX_VALUE,5},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,5,Integer.MAX_VALUE}
    
    };
    Graph graph = new Graph(vertexs, edges);
    graph.printGraph();
    graph.search();
  }
  
}

위 내용은 Java에서 최단 경로 알고리즘을 위한 Dijkstra 알고리즘 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!