인공 신경망은 동물 신경망의 행동 특성을 모방하고 분산 병렬 정보 처리를 수행하는 알고리즘 수학적 모델입니다. 이러한 종류의 네트워크는 다수의 내부 노드 간의 상호 연결된 관계를 조정하여 정보 처리 목적을 달성하기 위해 시스템의 복잡성에 의존하며 자체 학습 및 적응 기능을 갖추고 있습니다. 이 글은 주로 신경망의 이론적 기초와 Python 구현에 대한 자세한 설명을 소개하며, 도움이 필요한 친구들이 참고할 수 있기를 바랍니다.
1. 다층 순방향 신경망
다층 순방향 신경망은 출력층, 은닉층, 출력층의 세 부분으로 구성됩니다.
입력층. 훈련 세트로 구성됩니다. 인스턴스 특징 벡터가 전달되고, 연결 노드의 가중치를 통해 다음 레이어로 전달됩니다. 이전 레이어의 출력은 다음 레이어의 입력입니다. 입력 레이어가 하나 뿐이고 출력 레이어도 하나뿐입니다.
입력 레이어를 제외하고 은닉 레이어 수와 출력 레이어 수의 합은 n이므로 신경망을 n 레이어 신경망이라고 합니다. 다음 그림은
한 레이어의 가중 합산, 비선형 방정식에 따른 변환 및 출력을 보여줍니다. 이론적으로 숨겨진 레이어가 충분하고 훈련 세트가 충분히 크다면 모든 방정식을 시뮬레이션할 수 있습니다.
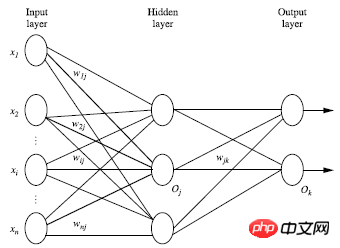
2. 신경망 구조 설계
사용 신경망을 만들기 전에 신경망의 레이어 수와 각 레이어의 단위 수를 결정해야 합니다.
속도를 높이려면; 학습 과정에서 특징 벡터는 일반적으로 입력 레이어에 전달되기 전에 0과 1 사이로 표준화되어야 합니다.
이산 유형 변수는 고유값에 해당하는 각 입력 단위에 할당된 가능한 값으로 인코딩될 수 있습니다
예를 들어 고유값 A는 세 개의 값(a0, a1, a2)을 가질 수 있으며, 3개의 입력 단위를 사용하여 A를 나타낼 수 있습니다
A=a0이면 a0을 나타내는 단위 값은 1이고 나머지는 0입니다.
A=a1이면 a1을 나타내는 단위 값은 1이고 나머지는 0입니다.
A=a2인 경우 a2를 나타내는 단위 값은 0 1이고 나머지는 0입니다. 분류 문제와 회귀 문제를 모두 해결합니다. 분류 문제의 경우 두 개의 범주가 있는 경우 하나의 출력 단위(0과 1)를 사용하여 두 개의 범주를 각각 나타낼 수 있습니다. 두 개 이상의 범주가 있는 경우 각 범주는 하나의 출력 단위로 표시되므로 단위 수는 다음과 같습니다. 출력 레이어의 수량은 일반적으로 하나의 카테고리와 같습니다.
최적의 히든 레이어 수를 설계하는 명확한 규칙은 없습니다. 실험은 일반적으로 실험 테스트 오류와 정확성을 기반으로 개선됩니다. 
정확도는 어떻게 계산하나요? 가장 간단한 방법은 훈련 세트와 테스트 세트를 사용하여 모델을 얻는 것입니다. 테스트 세트는 테스트 결과를 얻기 위해 모델에 입력됩니다. 정확도를 얻기 위한 테스트 세트입니다. 기계학습 분야에서 흔히 사용되는 방법은 교차 검증 방법입니다. 데이터 세트는 2개 부분으로 나누어지지 않고 10개 부분으로 나눌 수 있습니다.
첫 번째: 첫 번째 부분은 테스트 세트로 사용되고 나머지 9개 부분은 훈련 세트로 사용됩니다. 시간: 두 번째 부분은 테스트 세트로 사용되고 나머지 9개 부분은 훈련 세트로 사용됩니다....
10번의 훈련 후에 10세트의 정확도가 얻어집니다. 10개의 데이터 세트가 얻어졌습니다. 여기서 10은 특별한 경우입니다. 일반적으로 데이터를 k개 부분으로 나누는 알고리즘을 K-foldcrossvalidation이라고 합니다. 즉, 매번 k개 부분 중 하나를 테스트 세트로 선택하고 나머지 k-1개 부분을 사용하는 것입니다. 훈련 세트를 k번 반복하여 최종적으로 평균 정확도를 얻는 것이 더 과학적이고 정확한 방법입니다.

반복을 통해 훈련 세트의 인스턴스를 처리합니다. 신경망을 통과한 후 예측 값과 실제 값의 차이를 비교합니다. 출력 레이어 = >숨겨진 레이어 =>입력 레이어) 오류를 최소화하고 각 연결의 가중치를 업데이트합니다. 4.1, 알고리즘에 대한 자세한 소개
입력: 데이터 세트, 학습 속도, 다중 레이어;
출력: 훈련된 신경망 가중치 및 편향 초기화: -1과 1(또는 기타) 사이에서 무작위로 초기화되며 각 단위는 각 훈련 인스턴스 X에 대해 편향을 갖습니다. 1, 입력 레이어에서 전달: 신경망 회로도와 결합된 분석:히든 레이어에서 출력 레이어로: 

두 수식을 요약하면 다음과 같습니다.

Ij는 현재 레이어의 단위 값, Oi는 이전 레이어의 단위 값, wij는 두 레이어를 연결하는 가중치 값입니다. 두 개의 단위 값 sitaj는 각 레이어의 편향 값입니다. 각 레이어의 출력에 대해 비선형 변환을 수행해야 합니다. 회로도는 다음과 같습니다.

현재 레이어의 출력은 Ij이고, f는 활성화 함수라고도 알려진 비선형 변환 함수입니다.

즉, 각 레이어의 출력은 다음과 같습니다.

이렇게 하면 순방향 입력값을 통해 각 레이어의 출력값을 얻을 수 있습니다.
2. 오류 기반 역방향 전송 출력 계층의 경우: Tk는 실제 값이고 Ok는 예측 값입니다.

편향된 업데이트:

3. 종료 조건
편향된 업데이트가 특정 임계값보다 낮습니다.  예측 오류율이 특정 임계값보다 낮습니다.
예측 오류율이 특정 임계값보다 낮습니다.
 위에서 언급한 비선형 변환 함수 f는 일반적으로 두 가지 함수를 사용할 수 있습니다:
위에서 언급한 비선형 변환 함수 f는 일반적으로 두 가지 함수를 사용할 수 있습니다:
(1) tanh(x) 함수:
tanh(x)=sinh(x)/cosh(x)
sinh(x)=(exp(x)-exp(-x))/2
cosh(x)=(exp(x)+exp(-x))/2
(2) 위에서 사용된 논리 함수 이 기사는 논리 함수입니다
5. BP 신경망의 Python 구현
은 비선형 변환 함수를 정의하기 위해 먼저 numpy 모듈을 가져와야 합니다
import numpy as np
. 함수도 필요하므로 함께 정의
def tanh(x): return np.tanh(x) def tanh_deriv(x): return 1.0 - np.tanh(x)*np.tanh(x) def logistic(x): return 1/(1 + np.exp(-x)) def logistic_derivative(x): return logistic(x)*(1-logistic(x))
객체 지향을 사용하고 주로 비선형 함수를 선택하여 BP 신경망의 형태(레이어 수, 각 레이어에 단위 수)를 설계하고, 가중치를 초기화합니다. 레이어는 각 레이어의 단위 수를 포함하는 목록입니다.
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
"""
:param layers: A list containing the number of units in each layer.
Should be at least two values
:param activation: The activation function to be used. Can be
"logistic" or "tanh"
"""
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)알고리즘 구현
def fit(self, X, y, learning_rate=0.2, epochs=10000):
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1]+1])
temp[:, 0:-1] = X
X = temp
y = np.array(y)
for k in range(epochs):
i = np.random.randint(X.shape[0])
a = [X[i]]
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)예측 구현
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0]+1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return a예측을 위해 일련의 숫자를 제공하고, 위의 프로그램 파일은 BP
라는 이름으로 저장됩니다.
아아아아 결과는 다음과 같습니다. 간단한 신경망을 구현하는 JavaScript 그림과 텍스트로 네트워크 알고리즘에 대한 자세한 설명위 내용은 신경망의 이론적 기초와 Python 구현 방법에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!