PHP 기반 시뮬레이션 곡선 알고리즘에 대한 자세한 설명-PHP 튜토리얼-php.cn

PHP 기반 시뮬레이션 곡선 알고리즘에 대한 자세한 설명

小云云

풀어 주다： 2023-03-19 20:28:01

원래의

1782명이 탐색했습니다.

이 글은 주로 PHP를 기반으로 한 다중 선형 회귀 시뮬레이션 곡선 알고리즘을 소개하며, 관련 PHP 구현 기술을 구체적인 예를 들어 설명합니다. 그것이 모두에게 도움이 되기를 바랍니다.

다중 선형 회귀 모델: y = b1x1 + b2x2 + b3x3 +... +bnxn;

우리는 일련의 데이터를 기반으로 합니다: 유사 arr_x = [[1, 2, 3, 4, 5] , [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; arr_y = [5, 10, 15]; 우리가 최종적으로 얻고자 하는 것은 값을 포함하는 배열입니다. b1에서 bn까지;

방법: 최소 제곱법을 사용합니다

공식: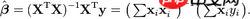공식의 전반부만 사용합니다. 즉, 행렬을 사용하여 계산합니다

공식의 X는 arr_x이며 다음과 같이 할 수 있습니다. 2차원 배열을 행렬로 간주하고, 수식에서 y는 arr_y이므로 행렬(5, 10, 15)로 간주할 수도 있지만 세로로 작성해야 합니다.

그런 다음 공식에 따라 행렬 곱셈, 전치 및 반전을 사용해야 한다는 것을 알게 되므로 다음 코드가 하나씩 제공됩니다.

public function get_complement($data, $i, $j) {
  /* x和y为矩阵data的行数和列数 */
  $x = count($data);
  $y = count($data[0]);
  /* data2为所求剩余矩阵 */
  $data2 =[];
  for ($k = 0; $k < $x -1; $k++) {
    if ($k < $i) {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k][$kk];
        } else {
          $data2[$k][$kk] = $data[$k][$kk +1];
        }
      }
    } else {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k +1][$kk];
        } else {
          $data2[$k][$kk] = $data[$k +1][$kk +1];
        }
      }
    }
  }
  return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
  $ans = 0;
  if (count($data[0]) === 2) {
    $ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
  } else {
    for ($i = 0; $i < count($data[0]); $i++) {
      $data_temp = $this->get_complement($data, 0, $i);
      if ($i % 2 === 0) {
        $ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
      } else {
        $ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
      }
    }
  }
  return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      if (($i + $j) % 2 === 0) {
        $data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
      } else {
        $data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
      }
    }
  }
  return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
  $i = count($data);
  $j = count($data[0]);
  $data2 =[];
  for ($k2 = 0; $k2 < $j; $k2++) {
    for ($k1 = 0; $k1 < $i; $k1++) {
      $data2[$k2][$k1] = $data[$k1][$k2];
    }
  }
  /*将矩阵转置便可得到伴随矩阵*/
  return $data2;
}
/*求矩阵的逆，输入参数为原矩阵*/
public function inv($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  $det_val = $this->cal_det($data);
  $data2 = $this->ajoint($data);
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      $data2[$i][$j] = $data2[$i][$j] / $det_val;
    }
  }
  return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
  /*$data1 为左乘矩阵*/
  $m1 = count($data1);
  $n1 = count($data1[0]);
  $m2 = count($data2);
  $n2 = count($data2[0]);
  $data_new =[];
  if ($n1 !== $m2) {
    return false;
  } else {
    for ($i = 0; $i <= $m1 -1; $i++) {
      for ($k = 0; $k <= $n2 -1; $k++) {
        $data_new[$i][$k] = 0;
        for ($j = 0; $j <= $n1 -1; $j++) {
          $data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
        }
      }
    }
  }
  return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
  $final =[];
  $arr_x_t = $this->trans($arr_x);
  $result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
  foreach ($result as $key => $val) {
    foreach ($val as $_k => $_v) {
      $final[] = $_v;
    }
  }
  return $final;
}

로그인 후 복사

마지막 getParams() 방법이 마지막 방법입니다. b 매개변수 배열인 경우 2차원 배열 arr_x와 1차원 배열 arr_y를 전달하면 됩니다.

일반적으로 빅데이터를 기반으로 다음과 같은 발전과 동향을 시뮬레이션하고 예측하는 빅데이터 분석에 사용됩니다.