CSS는 모든 크기, 방향 및 각도의 화살표 코드를 구현합니다.

이 기사에서는 CSS를 사용하여 모든 크기, 방향 및 각도의 화살표를 구현하는 데 대한 관련 정보를 주로 소개합니다. 이제 편집자는 이를 여러분과 공유하고 참고할 수 있기를 바랍니다. 당신을 도울 수 있습니다.

웹 개발에서는 드롭다운 화살표

나 오른쪽 화살표

와 같은 화살표가 자주 사용됩니다. 일반적으로 CSS로 구현됩니다:

{  
        display: inline-block;  
        margin: 72px;  
        border-top: 24px solid;
        border-right: 24px solid;  
        width: 120px;
        height: 120px;  
        transform: rotate(45deg); 
    }

이는 p의 border-top과 border-right를 사용한 다음 p를 회전시켜 달성되기 때문입니다.

모든 각도의 화살표

질문입니다. 120도 각도의 화살표가 필요한 경우 어떻게 해야 합니까? border-top과 border-right는 항상 90도이므로 회전만으로는 작동하지 않습니다. 먼저 p를 45도 회전하여 마름모로 만든 다음 어떤 각도에 도달하도록 늘려서 어떤 각도에서든 화살표를 얻을 수 있습니다. 회전(rotation)과 스케일링(scaling) 두 가지 변환을 사용하므로 변환 행렬 transform: 행렬(a,b,c,d,e,f)를 사용해야 합니다. 여기에 있는 6개의 변수는 3차원 변환 행렬을 형성합니다.transform: matrix(a,b,c,d,e,f) 这个变换矩阵。 这里的6个变量组成了一个3介的变换矩阵

任意点p(x,y)的平移， 旋转， 伸缩变换以及他们的各种组合都可以通过这个变换矩阵做到：

注：这里用齐次坐标 来表达一个点。 简单说就是p(x, y) 表示为p'(x', y', 1)

平移矩阵

v(x, y) 沿着x轴平移tx， 沿着y轴平移ty。 则有：

x' = x + tx
y' = y + ty

所以平移矩阵：

旋转矩阵

v(x, y) 点绕原点旋转θ到v'(x', y')

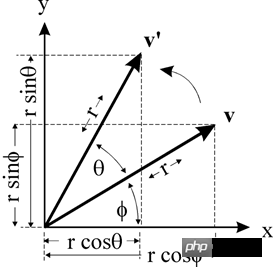
则有：

x = r * cos(ϕ )
y = r * sin(ϕ )

x' = r * cos(θ + ϕ) = r * cos(θ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // 余弦公式
y' = r * sin(θ + ϕ) = r * sin(θ) * cos(ϕ) + r * cos(θ) * sin(ϕ ) // 正弦公式

所以：

x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos(θ)

所以旋转矩阵：

伸缩矩阵

假设x轴，y轴的伸缩率分别是kx， ky。 则有：

x' = x * kx
y' = y * ky

所以：

复合变换

如果是对p(x, y)先平移(变换矩阵A)， 然后旋转(变换矩阵B)， 然后伸缩(变换矩阵C)呢?

p' =C(B(Ap)) ==> p' = (CBA)p //矩阵乘法结合率

现在任意角度o的箭头就很简单了：

先把p旋转45度 成为 菱形， 变换为 M1 伸缩x轴， y轴 :

x' = size * cos(o/2) = x * √2 *  cos(o/2)
y' = size * sin(o/2) = y *  √2  * sin(o/2)

即： kx = √2 * cos(o/2); ky = √2 * sin(o/2) 这样就得到了任意角度的箭头。 变换为 M2

如果箭头的方向不是指向右侧， 在进行一次旋转就可以得到任意方向的箭头。变换为 M3

那么由于 p' =C(B(Ap)) ==> p' = (CBA)p이 변환 행렬을 통해 모든 점 p(x,y)의 이동, 회전, 확장 변환 및 다양한 조합을 달성할 수 있습니다.

참고: 여기서는 동차를 사용하여 점을 표현합니다. 좌표. 간단히 말해서 p(x, y)는 p'(x', y', 1)

Translation 행렬

v(x, y)는 x축을 따라 tx를 이동하고 y축을 따라 ty를 이동합니다. . 그러면 다음과 같습니다:

x' = x + tx

y' = y + ty

그래서 변환 행렬:

rotation 행렬

v(x, y) 점이 회전합니다. θ 원점을 중심으로 v'(x', y')

그러면:

x = r * cos(ψ )

y = r * sin(ψ )

x' = r * cos(θ + ψ) = r * cos(θ) * cos(² ) - r * sin(θ) * sin(² ) // 코사인 공식

y' = r * sin(θ + ф) = r * sin(θ) * cos(ф) + r * cos(θ ) * sin (ф ) // 사인 공식

So:

x' = x * cos(θ) - y * sin(θ)y' = x * sin(θ) + y * cos (θ)

회전 행렬은 다음과 같습니다.

스트레칭 행렬 x축과 y축의 크기 조정 비율이 각각 kx와 ky라고 가정합니다. 다음은 다음과 같습니다: x' = x * kx복합 변환p(x, y)가 먼저 변환되는 경우 행렬 A ), 회전(변환 행렬 B), 그런 다음 늘이기(변환 행렬 C)?M1즉: kx = √ 2 * cos (o/2); ky = √2 * sin(o/2) 이것은 어떤 각도에서도 화살표를 제공합니다. 로 변신 화살표 방향이 오른쪽이 아닌 경우 회전을 하면 어떤 방향으로든 화살표를 얻을 수 있습니다. 로 변환됩니다. 그러면 p' =C(B(Ap)) ==> p' = (CBA)p이므로 먼저 M3 M1을 계산할 수 있습니다. p에 대한 해당 변환을 수행하면 어떤 각도와 방향에서도 화살표를 얻을 수 있습니다. p의 너비와 높이는 화살표의 변 길이를 조정하면 임의의 변 길이로 화살표를 얻을 수 있습니다. 사용 편의성을 위해 이 화살표는 React 구성 요소로 캡슐화됩니다. ㅋㅋㅋ nametypedefault

	y' = y * ky	그래서:
p' =C(B(Ap)) ==> p' = (CBA)p //행렬 곱셈 조합 비율	이제 모든 각도 o의 화살표는 매우 간단합니다.	먼저 p를 45도 회전하여 마름모로 변환하고	로 변환합니다. x축, y축:
npm install rc-arrow --save	M2		M3
M2			React 구성 요소

🎜설명 🎜🎜🎜🎜🎜🎜degree🎜🎜number🎜🎜90🎜🎜화살표의 각도, 각도계🎜🎜🎜🎜offsetDegree🎜🎜number🎜🎜0🎜🎜화살표의 방향, 기본값은 오른쪽🎜 🎜 🎜🎜color🎜🎜string 🎜🎜-🎜🎜화살표 색상🎜🎜🎜🎜size🎜🎜string🎜🎜10px🎜🎜화살표 길이🎜🎜🎜🎜

安装使用

npm install rc-arrow --save

import Arrow from 'rc-arrow'

class Hw extends Component {
    render() {
        return (
            <Arrow size="20px" color="red"/>
        )
    }
}

相关推荐：

纯CSS3实现网页中常见的小箭头实例

用css3制作网页中常见的小箭头的方法

JavaScript箭头函数的用法介绍

위 내용은 CSS는 모든 크기, 방향 및 각도의 화살표 코드를 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!