JavaScript_javascript 팁에서 수치 정밀도 손실 문제를 해결하는 방법

이 글은 세 부분으로 나누어져 있습니다

• JS 수치 정밀도 손실과 관련된 몇 가지 일반적인 문제
• JS 수치 정밀도가 떨어지는 이유
• 솔루션(하나의 객체, 하나의 기능)

1. JS 디지털 정밀도 손실의 대표적인 문제점

1. 두 개의 간단한 부동 소수점 숫자 추가

0.1 + 0.2 != 0.3 // true

이것은 실제로 Firebug 문제가 아닙니다. 경고를 사용해 볼 수 있습니다(하하, 농담입니다).

Java 연산 결과 보기

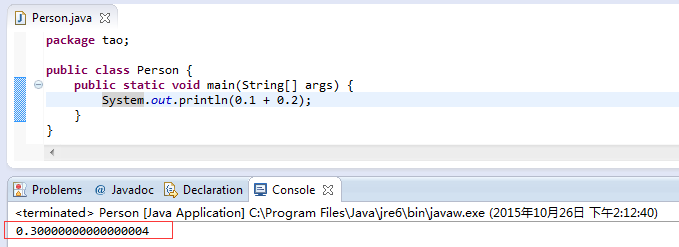
파이썬을 다시 살펴보세요

2. 큰 정수 연산

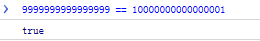
16자리 숫자와 17자리 숫자가 같다는 것은 말이 되지 않습니다.

또 다른 예

var x = 9007199254740992
x + 1 == x // ？

결과 보기

세 가지 견해가 다시 전복되었습니다.

3. toFixed 는 반올림되지 않습니다. (Chrome)

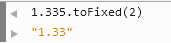
Chrome 가격이 다른 브라우저와 일치하지 않는 온라인 사례가 있었습니다

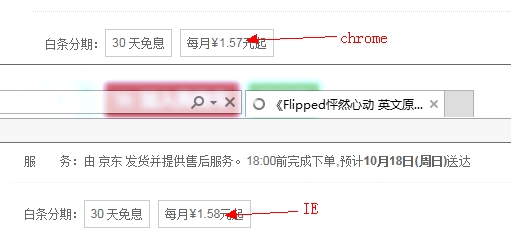
2. JS 숫자의 정밀도가 떨어지는 이유

컴퓨터의 바이너리 구현 및 비트 제한으로 인해 유한하게 표현할 수 없는 일부 숫자가 제한됩니다. 파이 3.1415926..., 1.3333... 등과 같은 일부 무리수를 유한하게 표현할 수 없는 것과 같습니다. JS는 IEEE 754 사양을 따르고 배정밀도 저장소를 사용하며 64비트를 차지합니다. 사진과 같이

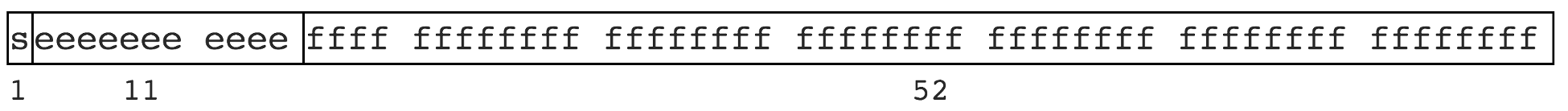
의미

• 부호 비트를 표현하기 위해 1비트가 사용됩니다
• 지수를 표현하기 위해 11비트가 사용됩니다
• 52비트는 가수를 나타냅니다

부동 소수점 숫자(예:

)

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

이때 반올림은 십진수만 흉내낼 수 있는데, 이진수는 0과 1 두 개의 숫자만 있어서 반올림하면 0과 1이 됩니다. 이는 컴퓨터의 일부 부동 소수점 연산에서 오류 및 정밀도 손실의 근본 원인입니다.

큰 정수의 정밀도 손실은 본질적으로 부동 소수점 숫자의 정밀도와 동일합니다. 최대 가수 자릿수는 52입니다. 따라서 JS에서 정확하게 표현할 수 있는 가장 큰 정수는 Math.pow(2, 53)입니다. , 십진수로는 9007199254740992입니다.

9007199254740992보다 큰 경우 정밀도가 떨어질 수 있습니다

9007199254740992  >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

사실

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

결과는 사진과 같습니다

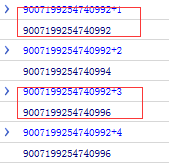
위에서 보면 유한해 보이는 숫자가 컴퓨터의 이진수 표현에서는 무한하다는 것을 알 수 있습니다. 저장 자릿수 제한으로 인해 "반올림"이 발생하고 정밀도 손실이 발생합니다.

3. 해결 방법

정수의 경우 프런트엔드 문제가 발생할 확률은 상대적으로 낮을 수 있습니다. 결국 연산 결과가 Math.pow(2, 53)를 초과하지 않는 한 매우 큰 정수를 사용해야 하는 비즈니스 요구는 거의 없습니다. 정확성은 손실되지 않습니다.

소수점의 경우 프런트엔드에서 문제가 발생할 가능성이 여전히 많습니다. 특히 일부 전자상거래 웹사이트에서 금액과 같은 데이터가 포함되는 경우 더욱 그렇습니다. 해결 방법: 소수를 정수에 넣은 다음(곱하기) 다시 원래의 배수로 줄입니다(나누기)

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

다음은 소수 덧셈, 뺄셈, 곱셈, 나눗셈 연산에서 정밀도 손실을 방지하기 위해 작성한 개체입니다. 물론 변환된 정수는 여전히 9007199254740992를 초과할 수 없습니다.

/**
 * floatObj 包含加减乘除四个方法，能确保浮点数运算不丢失精度
 *
 * 我们知道计算机编程语言里浮点数计算会存在精度丢失问题（或称舍入误差），其根本原因是二进制和实现位数限制有些数无法有限表示
 * 以下是十进制小数对应的二进制表示
 *  0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
 *  0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
 * 计算机里每种数据类型的存储是一个有限宽度，比如 JavaScript 使用 64 位存储数字类型，因此超出的会舍去。舍去的部分就是精度丢失的部分。
 *
 * ** method **
 * add / subtract / multiply /divide
 *
 * ** explame **
 * 0.1 + 0.2 == 0.30000000000000004 （多了 0.00000000000004）
 * 0.2 + 0.4 == 0.6000000000000001 （多了 0.0000000000001）
 * 19.9 * 100 == 1989.9999999999998 （少了 0.0000000000002）
 *
 * floatObj.add(0.1, 0.2) >> 0.3
 * floatObj.multiply(19.9, 100) >> 1990
 *
 */
var floatObj = function() {

 /*
  * 判断obj是否为一个整数
  */
 function isInteger(obj) {
  return Math.floor(obj) === obj
 }

 /*
  * 将一个浮点数转成整数，返回整数和倍数。如 3.14 >> 314，倍数是 100
  * @param floatNum {number} 小数
  * @return {object}
  * {times:100, num: 314}
  */
 function toInteger(floatNum) {
  var ret = {times: 0, num: 0}
  if (isInteger(floatNum)) {
   ret.num = floatNum
   return ret
  }
  var strfi = floatNum + ''
  var dotPos = strfi.indexOf('.')
  var len = strfi.substr(dotPos+1).length
  var times = Math.pow(10, len)
  var intNum = parseInt(floatNum * times + 0.5, 10)
  ret.times = times
  ret.num = intNum
  return ret
 }

 /*
  * 核心方法，实现加减乘除运算，确保不丢失精度
  * 思路：把小数放大为整数（乘），进行算术运算，再缩小为小数（除）
  *
  * @param a {number} 运算数1
  * @param b {number} 运算数2
  * @param digits {number} 精度，保留的小数点数，比如 2, 即保留为两位小数
  * @param op {string} 运算类型，有加减乘除（add/subtract/multiply/divide）
  *
  */
 function operation(a, b, digits, op) {
  var o1 = toInteger(a)
  var o2 = toInteger(b)
  var max = o1.times > o2.times ? o1.times : o2.times
  var result = null
  switch (op) {
   case 'add':
    result = o1.num + o2.num
    break
   case 'subtract':
    result = o1.num - o2.num
    break
   case 'multiply':
    result = o1.num * o2.num
    break
   case 'divide':
    result = o1.num / o2.num
    break
  }
  return result / max
 }

 // 加减乘除的四个接口
 function add(a, b, digits) {
  return operation(a, b, digits, 'add')
 }
 function subtract(a, b, digits) {
  return operation(a, b, digits, 'subtract')
 }
 function multiply(a, b, digits) {
  return operation(a, b, digits, 'multiply')
 }
 function divide(a, b, digits) {
  return operation(a, b, digits, 'divide')
 }

 // exports
 return {
  add: add,
  subtract: subtract,
  multiply: multiply,
  divide: divide
 }

}();

ToFixed는 다음과 같이 고정됩니다

// toFixed 修复
function toFixed(num, s) {
 var times = Math.pow(10, s)
 var des = num * times + 0.5
 des = parseInt(des, 10) / times
 return des + ''
}

이상은 JavaScript 수치 정밀도 손실 문제에 대한 것입니다. 일반적인 문제를 분석하고, 수치 정밀도 손실의 원인을 분석하고, 모든 사람의 학습에 도움이 되기를 바랍니다.