PHP는 몇 가지 일반적인 정렬 알고리즘을 구현합니다.
교환 정렬: 교환 정렬의 기본 아이디어는 두 레코드의 키 값을 비교하는 것입니다. 두 레코드의 키 값이 역순이면 두 레코드를 더 작은 레코드로 교환합니다. 키 값이 순서대로 앞으로 이동합니다. 키 값이 큰 레코드는 순서의 뒤로 이동합니다. 1. 버블 정렬
버블 정렬(버블 정렬, 대만어 번역: 버블 정렬 또는 버블 정렬)은 간단한
정렬 알고리즘
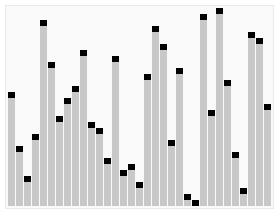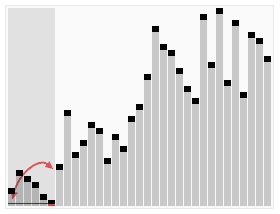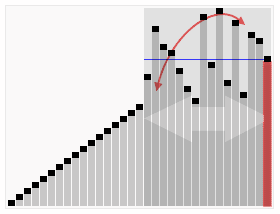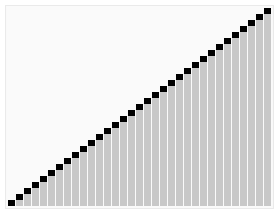
입니다. 정렬할 시퀀스를 반복적으로 살펴보며 한 번에 두 요소를 비교하고 순서가 잘못된 경우 교체합니다. 더 이상 교환이 필요하지 않을 때까지 어레이 방문 작업이 반복됩니다. 이는 어레이가 정렬되었음을 의미합니다. 이 알고리즘의 이름은 작은 요소가 스와핑을 통해 배열의 맨 위로 천천히 "부동"된다는 사실에서 유래되었습니다. 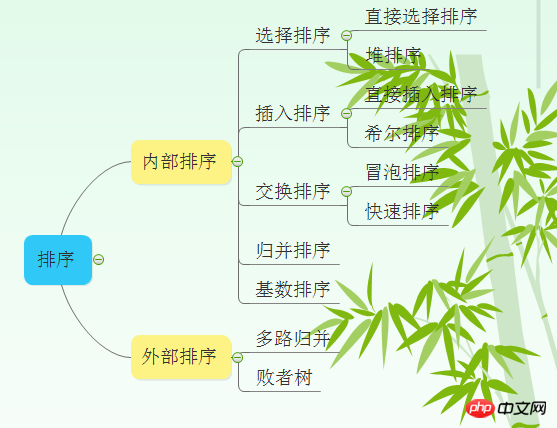
인접한 요소를 비교합니다. 첫 번째 것이 두 번째 것보다 크면 둘 다 교환하세요.
시작의 첫 번째 쌍부터 끝의 마지막 쌍까지 인접한 요소의 각 쌍에 대해 동일한 작업을 수행합니다. 이때 마지막 요소가 가장 큰 숫자가 되어야 합니다.
마지막 요소를 제외한 모든 요소에 대해 위 단계를 반복합니다.
비교할 숫자 쌍이 더 이상 없을 때까지 매번 요소 수를 줄여 위 단계를 계속 반복하세요.
- 버블 정렬은 이해하기 가장 간단하지만 시간 복잡도(O(n^2))도 가장 큰 것 중 하나입니다. 구현 코드는 다음과 같습니다.
<br/>
로그인 후 복사로그인 후 복사로그인 후 복사$arr=array(1,43,54,62,21,66,32,78,36,76,39) function
getpao(- $arr
) {
$len
=- count
($arr); //비워두기 설정
//이 레이어 루프는 버블링이 필요한 라운드 수를 제어합니다
for
(- $i
=1;$i<$len;$i++) //이 레이어는 반복에 사용됩니다. 숫자에 필요한 횟수를 제어하려면 라운드마다 비교 예정
for($k=0;$k<$len-$i; $k++)
{
if($arr[$k]> $arr[$k+1] )
{
$tmp=$arr[ $k+1];
$arr[$k+1]=$arr[$k];
}}}} $ arr; 2. Quick sort
소개:
- Quick Sort는
Tony Hall이 개발한 정렬 알고리즘입니다. 평균적으로 n
항목을 정렬하려면 Ο - (
n log n
)번의 비교가 필요합니다. 최악의 경우에는 Ο - (
n2) 비교가 필요하지만 이런 상황은 흔하지 않습니다. 실제로 퀵 정렬은 내부 루프가 대부분의 아키텍처에서 효율적으로 구현될 수 있고 대부분의 실제 데이터에서 2차 항의 가능성이 필요한 시간을 줄이는 설계 선택을 지시합니다. 단계:
시퀀스에서 "피벗"이라는 요소를 선택합니다.
시퀀스를 재정렬합니다. 피벗 값보다 작은 모든 요소는 피벗 앞에 배치되고 피벗보다 큰 모든 요소는 값은 베이스 뒤에 배치됩니다(같은 숫자가 양쪽에 올 수 있음). 이 파티션이 종료된 후 베이스는 시퀀스의 중간에 있습니다. 이것을 partition 작업이라고 합니다.
기본 값보다 작은 요소의 하위 배열과 기본 값보다 큰 요소의 하위 배열을 재귀적으로 정렬합니다.
퀵 정렬도 효율적인 정렬 알고리즘이고, 시간 복잡도도 O(nlogn)입니다. 코드는 다음과 같습니다:
functionquick_sort($arr) {
-
$ 길이 - =
count ($arr) 1) {
- ㅋㅋ >
//첫 번째 요소 선택
-
$base_num =
$arr [0]
//모두 탐색 눈금자를 제외한 요소를 크기에 따라 두 개의 배열에 넣습니다. -
= 배열 ();// 자보다 작은
$right_array = array
( );//
if($base_num > $arr[$i]) { //넣어 왼쪽 배열에
] else { 그렇죠 G i $ right_array
- [] =
$ ar [ $ i] }}
/ /The n 왼쪽에서도 동일한 정렬을 수행 및 오른쪽 배열 각각-
= Quick_sort($left_array)
$right_array = Quick_sort($right_array
) ; //왼쪽 눈금자를 오른쪽 눈금자와 병합
return array_merge($left_array, array($base_num), $right_array)
}
선택 정렬
선택 정렬에는 직접 선택 정렬과 힙 정렬의 두 가지 유형이 있습니다. 선택 정렬의 기본 아이디어는 매번 n-i+ 1 ( i=1,2,3,...,n-1) 레코드, 가장 작은 키 값을 가진 레코드를 순서대로 i 번째 레코드로 선택
3. 선택 정렬
소개:
선택 정렬은 간단하고 직관적인 정렬 알고리즘입니다. 작동 방식은 다음과 같습니다. 먼저 정렬되지 않은 시퀀스에서 가장 작은 요소를 찾아 정렬된 시퀀스의 시작 부분에 저장한 다음, 정렬되지 않은 나머지 요소에서 계속해서 가장 작은 요소를 찾아 정렬된 시퀀스의 끝에 넣습니다. 모든 요소가 정렬될 때까지 계속됩니다.
 <br/>
<br/>선택 정렬도 비교적 이해하기 쉽고, 시간 복잡도도 O(n^2)입니다. 구현 코드는 다음과 같습니다.
<br/>
로그인 후 복사로그인 후 복사로그인 후 복사[php] view plain 복사
<br/>
function select_sort($arr) {
//구현 아이디어 이중 루프가 완료되고 외부 제어 라운드 수는 현재 최소값입니다. 내부 레이어에서 제어하는 비교 횟수
//$i 현재 최소값의 위치, 비교에 참여해야 하는 요소
for ($i =0, $len=count($arr); -1 ; $i ++ ) { $i
; /$j는 현재 $i 다음의 요소와 비교되어야 합니다. ㅋㅋ ~ // $arr[$p] +
// 알려진 최소값을 비교에 사용해야 합니다.
//현재 최소값 위치가 결정되어 $p에 저장되었습니다. ㅋㅋㅋ ($ p !=
$i) {
$p- ];
[$p] = $arr[$i];
[$i] = $tmp;
//최종 결과 반환
return $arr
}
4. <br/>
소개:
스태킹 정렬(Heapsort)은 heap의 데이터 구조를 사용하여 설계된 정렬 알고리즘을 말합니다. 힙은 완전 이진 트리에 근접하면서 힙 속성을 동시에 만족하는 구조입니다. 즉, 하위 노드의 키 값이나 인덱스는 항상 더 작습니다(또는 더 큽니다). ) 상위 노드보다.
단계:
힙 정렬은 배열의 특성을 이용하여 지정된 인덱스에서 요소를 빠르게 찾는 스택 트리(힙)와 같은 데이터 구조를 사용하여 설계된 정렬 알고리즘을 말합니다. 힙은 큰 루트 힙과 작은 루트 힙으로 나누어지며 이는 완전한 이진 트리입니다. 큰 루트 힙의 요구 사항은 각 노드의 값이 해당 상위 노드의 값, 즉 A[PARENT[i]] >= A[i]보다 크지 않아야 한다는 것입니다. 배열의 비내림차순 정렬에서는 큰 루트 힙의 요구 사항에 따라 최대값이 힙의 맨 위에 있어야 하기 때문에 큰 루트 힙을 사용해야 합니다.
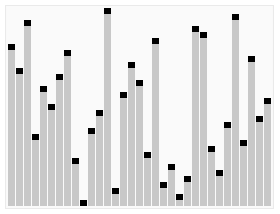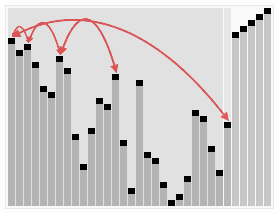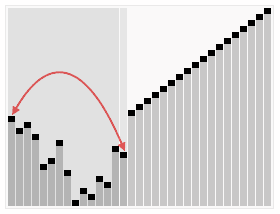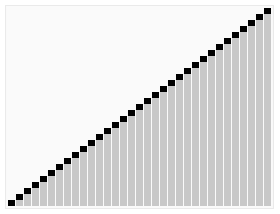
정렬 효과:

 <br/>
<br/>堆排序是一种高效的排序算法,它的时间复杂度是O(nlogn)。原理是:先把数组转为一个最大堆,然后把第一个元素跟第i元素交换,然后把剩下的i-1个元素转为最大堆,然后再把第一个元素与第i-1个元素交换,以此类推。实现代码如下:
function heapSort($arr) { $len = count($arr); // 先建立最大堆 for ($i = floor(($len - 1) / 2); $i >= 0; $i--) { $s = $i; $childIndex = $s * 2 + 1; while ($childIndex < $len) { // 在父、左子、右子中 ,找到最大的 if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1; } else { break; } } } // 从最后一个元素开始调整 for ($i = $len - 1; $i > 0; $i--) { $t = $arr[$i]; $arr[$i] = $arr[0]; $arr[0] = $t; // 调整第一个元素 $s = 0; $childIndex = 1; while ($childIndex < $i) { // 在父、左子、右子中 ,找到最大的 if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1; } else { break; } } } return $arr; }$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8]; print_r(bubbleSort($arr));로그인 후 복사<br/>
<br/>
插入排序
五、插入排序
介绍:
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
步骤:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素(已排序)大于新元素,将该元素移到下一位置
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置中
重复步骤2
 <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:[php]일반 보기copy
<br/>
function insert_sort($arr) {
//어떤 부분을 구별 정렬되었습니다
//정렬되지 않은 부분
//정렬해야 할 요소 중 하나를 찾으세요
//이 요소는 두 번째 요소에서 시작하여 정렬이 필요한 마지막 요소로 끝납니다
//루프를 사용하여 표시할 수 있습니다
//i 루프는 삽입해야 하는 요소를 매번 제어합니다. 삽입해야 하는 요소를 제어하면
//간접적으로 배열이 2개로 나누어졌습니다. , 그리고 아래 첨자가 현재 것(왼쪽에 있는 것)보다 작으면 정렬된 시퀀스입니다
for($i=1, $len=count($arr); $i <$ len; $i++) {
//비교해야 할 현재 요소 값을 가져옵니다.
$tmp = $arr[$i]
-
//내부 루프 비교 및 삽입 제어
for($j=$i- 1;$j>=0;$ j --) {
//$arr[$i];//삽입할 요소; $arr[$j] //비교할 요소
-
if( $tmp <$arr[$j]) {
-
- //다음 요소를 이전 요소와 교환
[$j ] $arr[$j] =
$ tmp- ;
} else {
//如果碰到不需要移动的元素
//由于是已经排序好是数组,则前面的就不需要再次比较了。
break;
}
}
}
//将这个元素 插入到已经排序好的序列内。
//返回
return $arr;
}
<br/>
로그인 후 복사로그인 후 복사로그인 후 복사六、希尔排序
介绍:
希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1、插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
2、但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位>
排序效果:
 <br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:
<br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:function shellSort($arr) { $len = count($arr); $stepSize = floor($len / 2); while ($stepSize >= 1) { for ($i = $stepSize; $i < $len; $i++) { if ($arr[$i] < $arr[$i - $stepSize]) { $t = $arr[$i]; $j = $i - $stepSize; while ($j >= 0 && $t < $arr[$j]) { $arr[$j + $stepSize] = $arr[$j]; $j -= $stepSize; } $arr[$j + $stepSize] = $t; } } // 缩小步长,再进行插入排序 $stepSize = floor($stepSize / 2); } return $arr; }$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8]; print_r(bubbleSort($arr));로그인 후 복사<br/>
七、归并排序
介绍:
归并排序(Merge sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(pide and Conquer)的一个非常典型的应用
步骤:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
排序效果:
 <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:我们先来看看主函数部分:
//交换函数function swap(array &$arr,$a,$b){ $temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp; }//归并算法总函数function MergeSort(array &$arr){ $start = 0; $end = count($arr) - 1; MSort($arr,$start,$end); }로그인 후 복사在总函数中,我们只调用了一个 MSort() 函数,因为我们要使用递归调用,所以将 MSort() 封装起来。
下面我们来看看 MSort() 函数:
function MSort(array &$arr,$start,$end){ //当子序列长度为1时,$start == $end,不用再分组 if($start < $end){ $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end] MSort($arr,$start,$mid); //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid] MSort($arr,$mid + 1,$end); //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end] Merge($arr,$start,$mid,$end); //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end] } }로그인 후 복사上面的 MSort() 函数实现将数组分半再分半(直到子序列长度为1),然后将子序列合并起来。
现在是我们的归并操作函数 Merge() :
//归并操作function Merge(array &$arr,$start,$mid,$end){ $i = $start; $j=$mid + 1; $k = $start; $temparr = array(); while($i!=$mid+1 && $j!=$end+1) { if($arr[$i] >= $arr[$j]){ $temparr[$k++] = $arr[$j++]; } else{ $temparr[$k++] = $arr[$i++]; } } //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中 while($i != $mid+1){ $temparr[$k++] = $arr[$i++]; } //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中 while($j != $end+1){ $temparr[$k++] = $arr[$j++]; } for($i=$start; $i<=$end; $i++){ $arr[$i] = $temparr[$i]; } }로그인 후 복사到了这里,我们的归并算法就完了。我们调用试试:
$arr = array(9,1,5,8,3,7,4,6,2); MergeSort($arr); var_dump($arr);
로그인 후 복사相关推荐:
위 내용은 PHP는 몇 가지 일반적인 정렬 알고리즘을 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7677
7677
 15
15
 1393
1393
 52
52
 1207
1207
 24
24
 91
91
 11
11
 73
73
 19
19
 Ubuntu 및 Debian용 PHP 8.4 설치 및 업그레이드 가이드
Dec 24, 2024 pm 04:42 PM
Ubuntu 및 Debian용 PHP 8.4 설치 및 업그레이드 가이드
Dec 24, 2024 pm 04:42 PM
PHP 8.4는 상당한 양의 기능 중단 및 제거를 통해 몇 가지 새로운 기능, 보안 개선 및 성능 개선을 제공합니다. 이 가이드에서는 Ubuntu, Debian 또는 해당 파생 제품에서 PHP 8.4를 설치하거나 PHP 8.4로 업그레이드하는 방법을 설명합니다.
 이전에 몰랐던 후회되는 PHP 함수 7가지
Nov 13, 2024 am 09:42 AM
이전에 몰랐던 후회되는 PHP 함수 7가지
Nov 13, 2024 am 09:42 AM
숙련된 PHP 개발자라면 이미 그런 일을 해왔다는 느낌을 받을 것입니다. 귀하는 상당한 수의 애플리케이션을 개발하고, 수백만 줄의 코드를 디버깅하고, 여러 스크립트를 수정하여 작업을 수행했습니다.
 PHP 개발을 위해 Visual Studio Code(VS Code)를 설정하는 방법
Dec 20, 2024 am 11:31 AM
PHP 개발을 위해 Visual Studio Code(VS Code)를 설정하는 방법
Dec 20, 2024 am 11:31 AM
VS Code라고도 알려진 Visual Studio Code는 모든 주요 운영 체제에서 사용할 수 있는 무료 소스 코드 편집기 또는 통합 개발 환경(IDE)입니다. 다양한 프로그래밍 언어에 대한 대규모 확장 모음을 통해 VS Code는
 JWT (JSON Web Tokens) 및 PHP API의 사용 사례를 설명하십시오.
Apr 05, 2025 am 12:04 AM
JWT (JSON Web Tokens) 및 PHP API의 사용 사례를 설명하십시오.
Apr 05, 2025 am 12:04 AM
JWT는 주로 신분증 인증 및 정보 교환을 위해 당사자간에 정보를 안전하게 전송하는 데 사용되는 JSON을 기반으로 한 개방형 표준입니다. 1. JWT는 헤더, 페이로드 및 서명의 세 부분으로 구성됩니다. 2. JWT의 작업 원칙에는 세 가지 단계가 포함됩니다. JWT 생성, JWT 확인 및 Parsing Payload. 3. PHP에서 인증에 JWT를 사용하면 JWT를 생성하고 확인할 수 있으며 사용자 역할 및 권한 정보가 고급 사용에 포함될 수 있습니다. 4. 일반적인 오류에는 서명 검증 실패, 토큰 만료 및 대형 페이로드가 포함됩니다. 디버깅 기술에는 디버깅 도구 및 로깅 사용이 포함됩니다. 5. 성능 최적화 및 모범 사례에는 적절한 시그니처 알고리즘 사용, 타당성 기간 설정 합리적,
 PHP에서 HTML/XML을 어떻게 구문 분석하고 처리합니까?
Feb 07, 2025 am 11:57 AM
PHP에서 HTML/XML을 어떻게 구문 분석하고 처리합니까?
Feb 07, 2025 am 11:57 AM
이 튜토리얼은 PHP를 사용하여 XML 문서를 효율적으로 처리하는 방법을 보여줍니다. XML (Extensible Markup Language)은 인간의 가독성과 기계 구문 분석을 위해 설계된 다목적 텍스트 기반 마크 업 언어입니다. 일반적으로 데이터 저장 AN에 사용됩니다
 문자열로 모음을 계산하는 PHP 프로그램
Feb 07, 2025 pm 12:12 PM
문자열로 모음을 계산하는 PHP 프로그램
Feb 07, 2025 pm 12:12 PM
문자열은 문자, 숫자 및 기호를 포함하여 일련의 문자입니다. 이 튜토리얼은 다른 방법을 사용하여 PHP의 주어진 문자열의 모음 수를 계산하는 방법을 배웁니다. 영어의 모음은 A, E, I, O, U이며 대문자 또는 소문자 일 수 있습니다. 모음이란 무엇입니까? 모음은 특정 발음을 나타내는 알파벳 문자입니다. 대문자와 소문자를 포함하여 영어에는 5 개의 모음이 있습니다. a, e, i, o, u 예 1 입력 : String = "Tutorialspoint" 출력 : 6 설명하다 문자열의 "Tutorialspoint"의 모음은 u, o, i, a, o, i입니다. 총 6 개의 위안이 있습니다
 PHP에서 늦은 정적 결합을 설명하십시오 (정적 : :).
Apr 03, 2025 am 12:04 AM
PHP에서 늦은 정적 결합을 설명하십시오 (정적 : :).
Apr 03, 2025 am 12:04 AM
정적 바인딩 (정적 : :)는 PHP에서 늦은 정적 바인딩 (LSB)을 구현하여 클래스를 정의하는 대신 정적 컨텍스트에서 호출 클래스를 참조 할 수 있습니다. 1) 구문 분석 프로세스는 런타임에 수행됩니다. 2) 상속 관계에서 통화 클래스를 찾아보십시오. 3) 성능 오버 헤드를 가져올 수 있습니다.
 php magic 방법 (__construct, __destruct, __call, __get, __set 등)이란 무엇이며 사용 사례를 제공합니까?
Apr 03, 2025 am 12:03 AM
php magic 방법 (__construct, __destruct, __call, __get, __set 등)이란 무엇이며 사용 사례를 제공합니까?
Apr 03, 2025 am 12:03 AM
PHP의 마법 방법은 무엇입니까? PHP의 마법 방법은 다음과 같습니다. 1. \ _ \ _ Construct, 객체를 초기화하는 데 사용됩니다. 2. \ _ \ _ 파괴, 자원을 정리하는 데 사용됩니다. 3. \ _ \ _ 호출, 존재하지 않는 메소드 호출을 처리하십시오. 4. \ _ \ _ get, 동적 속성 액세스를 구현하십시오. 5. \ _ \ _ Set, 동적 속성 설정을 구현하십시오. 이러한 방법은 특정 상황에서 자동으로 호출되어 코드 유연성과 효율성을 향상시킵니다.




 <br/>
<br/>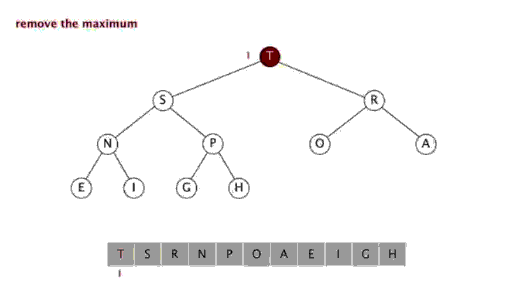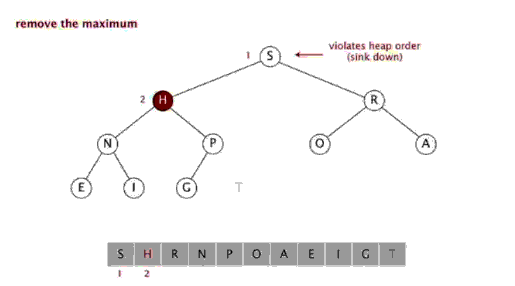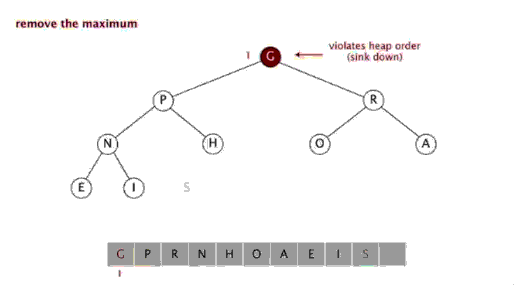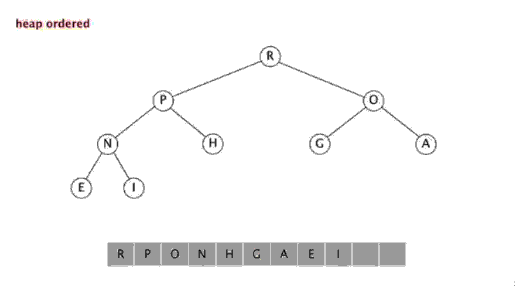
 <br/>
<br/> <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下: <br/>
<br/> <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下: