이진 힙은 특별한 종류의 힙입니다. 이진 힙은 완전 이진 트리 또는 대략 완전한 이진 트리입니다. 이진 힙에는 최대 힙과 최소 힙의 두 가지 유형이 있습니다. 상위 노드의 키 값은 다음과 같습니다. 항상 하위 노드의 키 값보다 크거나 같습니다. 최소 힙: 상위 노드의 키 값은 항상 하위 노드의 키 값보다 작거나 같습니다.
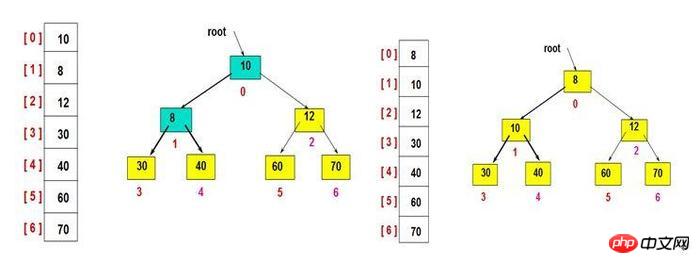
Small top heap-(인터넷 사진)
바이너리 힙은 일반적으로 배열로 표현됩니다(위 그림 참조). 예를 들어 배열에서 루트 노드의 위치는 0이고, n번째 위치의 자식 노드는 각각 2n+1과 2n+2에 있습니다. 따라서 0번째 위치의 자식 노드는 1과 2에 있고, 1의 자식 노드는 3과 4에 있습니다. 저장 방법을 사용하면 상위 노드와 하위 노드를 쉽게 찾을 수 있습니다.
여기에서는 구체적인 개념적 문제에 대해 자세히 다루지 않겠습니다. 바이너리 힙에 대해 궁금한 점이 있으면 이 데이터 구조를 잘 이해할 수 있습니다. 다음으로 위의 내용을 구현하고 해결하기 위해 PHP 코드를 사용하겠습니다. topN 문제의 차이점을 확인하려면 먼저 정렬 방법을 사용하여 구현하고 작동 방식을 확인하세요.
빠른 정렬 알고리즘을 사용하여 TopN 구현
//为了测试运行内存调大一点ini_set('memory_limit', '2024M');//实现一个快速排序函数function quick_sort(array $array){
$length = count($array); $left_array = array(); $right_array = array(); if($length <= 1){ return $array;
} $key = $array[0]; for($i=1;$i<$length;$i++){ if($array[$i] > $key){ $right_array[] = $array[$i];
}else{ $left_array[] = $array[$i];
}
} $left_array = quick_sort($left_array); $right_array = quick_sort($right_array); return array_merge($right_array,array($key),$left_array);
}//构造500w不重复数for($i=0;$i<5000000;$i++){ $numArr[] = $i;
}//打乱它们shuffle($numArr);//现在我们从里面找到top10最大的数var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());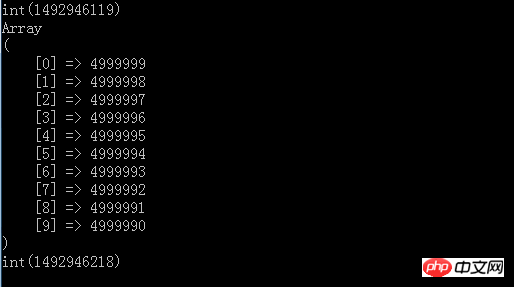
실행 후 결과
위에서 상위 10개의 결과가 출력되고 실행 시간이 99초 정도 출력되는 것을 볼 수 있는데, 이는 모든 숫자를 메모리에 로드할 수 있다면 5kw 또는 5억 숫자의 파일이 있는 경우 분명히 문제가 있을 것입니다.
이진 힙 알고리즘을 사용하여 TopN을 구현합니다
구현 과정
1, 먼저 10개 또는 100개의 숫자를 배열로 읽어옵니다. 이것이 topN 숫자입니다.
2. 이 배열에서 작은 상위 힙 구조를 생성하려면 이 함수를 호출하세요.
3. 파일이나 배열의 나머지 숫자를 모두 순서대로 탐색합니다.
4 탐색할 때마다 힙 위에 있는 요소와 크기를 비교합니다. 힙 상단에 있는 요소가 힙 상단에 있는 요소보다 크면 교체하세요.
5 힙의 상단 요소를 교체한 후 계속하려면 작은 상단 힙 생성 함수를 호출하세요. 가장 작은 것을 찾아야 하기 때문에 작은 상단 힙을 생성합니다.
6. 위의 4~5단계를 반복하여 모든 순회가 완료되면 작은 상단 힙 내부에 있는 것이 가장 큰 topN이 됩니다. 상단 힙은 항상 가장 작은 것을 제외하고 가장 큰 것을 남기며, 루트 노드가 왼쪽 및 오른쪽 노드보다 작은 한, 이 작은 상단 힙 조정도 매우 빠릅니다. 7. 알고리즘 복잡도 측면에서 최악의 시나리오는 숫자를 순회할 때마다 힙의 최상위로 교체되면 정렬 속도보다 빠른 10배의 조정이 필요하며, 모든 내용이 메모리에 읽혀지는 것은 선형 순회라는 것을 알 수 있습니다.
//生成小顶堆函数function Heap(&$arr,$idx){
$left = ($idx << 1) + 1; $right = ($idx << 1) + 2; if (!$arr[$left]){ return;
} if($arr[$right] && $arr[$right] < $arr[$left]){ $l = $right;
}else{ $l = $left;
} if ($arr[$idx] > $arr[$l]){ $tmp = $arr[$idx];
$arr[$idx] = $arr[$l]; $arr[$l] = $tmp;
Heap($arr,$l);
}
}//这里为了保证跟上面一致,也构造500w不重复数/*
当然这个数据集并不一定全放在内存,也可以在
文件里面,因为我们并不是全部加载到内存去进
行排序
*/for($i=0;$i<5000000;$i++){ $numArr[] = $i;
}//打乱它们shuffle($numArr);//先取出10个到数组$topArr = array_slice($numArr,0,10);//获取最后一个有子节点的索引位置//因为在构造小顶堆的时候是从最后一个有左或右节点的位置//开始从下往上不断的进行移动构造(具体可看上面的图去理解)$idx = floor(count($topArr) / 2) - 1;//生成小顶堆for($i=$idx;$i>=0;$i--){
Heap($topArr,$i);
}
var_dump(time());//这里可以看到,就是开始遍历剩下的所有元素for($i = count($topArr); $i < count($numArr); $i++){ //每遍历一个则跟堆顶元素进行比较大小
if ($numArr[$i] > $topArr[0]){ //如果大于堆顶元素则替换
$topArr[0] = $numArr[$i]; /*
重新调用生成小顶堆函数进行维护,只不过这次是从堆顶
的索引位置开始自上往下进行维护,因为我们只是把堆顶
的元素给替换掉了而其余的还是按照根节点小于左右节点
的顺序摆放这也就是我们上面说的,只是相对调整下,并
不是全部调整一遍
*/
Heap($topArr,0);
}
}
var_dump(time());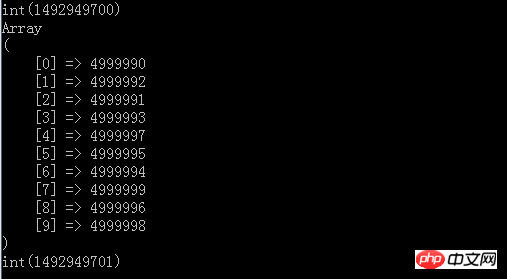 실행 후의 결과
실행 후의 결과
End 마지막으로 말씀드리고 싶은 것은
알고리즘 + 데이터 구조가 정말 매우 중요하다는 것입니다. 우리의 효율성을 향상시킵니다.
위 내용은 PHP 힙은 TopK 알고리즘 예제를 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!