이 기사의 내용은 Python을 사용하여 Jarque-Bera가 정규 분포를 따르는지 테스트하는 것입니다. 특정 참조 값이 필요합니다. 이를 참조할 수 있습니다.
정규 분포는 모집단의 정규 분포입니다. .성 테스트. 시퀀스가 정규 분포를 따르는 경우 JB 통계량:
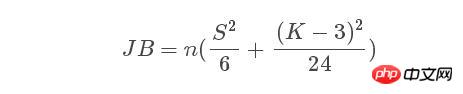
은 점근적으로 분포를 따릅니다. 여기서 n은 표본 크기이고, S와 K는 각각 확률 변수의 왜도와 첨도입니다. 계산 공식은 다음과 같습니다.
Python의 sicipy.stats에서 왜도 및 첨도 호출 의 함수는
이며, 여기서 첨도 공식은
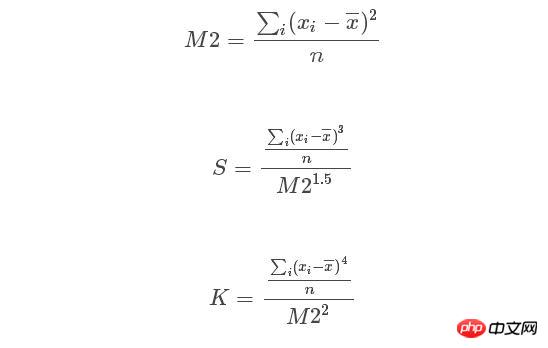 Python의 scipy 라이브러리에서 왜곡과 왜곡을 계산하는 공식을 구현하고 정규 분포 테스트를 설정해 보겠습니다.
Python의 scipy 라이브러리에서 왜곡과 왜곡을 계산하는 공식을 구현하고 정규 분포 테스트를 설정해 보겠습니다.
Codeimport numpy as npimport scipy.stats as statsdef self_JBtest(y):
# 样本规模n
n = y.size
y_ = y - y.mean() """
M2:二阶中心钜
skew 偏度 = 三阶中心矩 与 M2^1.5的比
krut 峰值 = 四阶中心钜 与 M2^2 的比
"""
M2 = np.mean(y_**2)
skew = np.mean(y_**3)/M2**1.5
krut = np.mean(y_**4)/M2**2
"""
计算JB统计量,以及建立假设检验
"""
JB = n*(skew**2/6 + (krut-3 )**2/24)
pvalue = 1 - stats.chi2.cdf(JB,df=2)
print("偏度:",stats.skew(y),skew)
print("峰值:",stats.kurtosis(y)+3,krut)
print("JB检验:",stats.jarque_bera(y)) return np.array([JB,pvalue])
y1 = stats.norm.rvs(size=10)
y2 = stats.t.rvs(size=1000,df=4)
print(self_JBtest(y1))
print(self_JBtest(y2))
=============== RESTART: C:\Users\tinysoft\Desktop\JB正态性检验.py =============== 偏度: 0.5383125387398069 0.53831253874 峰值: 2.9948926317585918 2.99489263176 JB检验: (0.48297818444514068, 0.78545737133644544) [ 0.48297818 0.78545737] 偏度: -1.0488825341925703 -1.04888253419 峰值: 13.40804986639119 13.4080498664 JB检验: (4697.0050126426095, 0.0) [ 4697.00501264 0. ]
위 내용은 Python은 Jarque-Bera가 정규 분포를 따르는지 테스트합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!