JS 이진 검색 트리 사용에 대한 자세한 설명
이번에는 JS 바이너리 검색트리 사용에 대해 자세히 설명하고, JS 바이너리 검색 트리 사용 시 주의사항은 무엇인지 살펴보겠습니다.
이진 트리란 무엇입니까
이진 트리는 트리의 각 노드가 최대 2개의 하위 노드만 가질 수 있음을 의미합니다이진 검색 트리란 무엇입니까
이진 트리를 기반으로 이진 검색 트리에는 추가 조건이 있습니다. 즉, 이진 트리에 값을 삽입할 때 삽입된 값이 현재 노드보다 작으면 왼쪽 노드에 삽입되고, 그렇지 않으면 삽입됩니다. 삽입 프로세스 중에 왼쪽 노드가 있거나 오른쪽 노드가 이미 존재하는 경우 새 노드를 만날 때까지 위의 규칙에 따라 계속 비교합니다.이진 검색 트리의 기능
고유한 데이터 구조로 인해 이진 검색 트리는 추가, 삭제 또는 검색 여부에 관계없이 O(h)의 시간 복잡도를 갖습니다. h는 이진 트리의 높이입니다. 따라서 이진 트리는 최대한 짧아야 합니다. 즉, 왼쪽 노드와 오른쪽 노드의 균형이 최대한 맞아야 합니다.이진 검색 트리 구축
이진 검색 트리를 구성하려면 먼저 이진 트리의 노드 클래스를 구성해야 합니다. 이진 트리의 특성을 보면 각 노드 클래스에는 왼쪽 노드와 오른쪽 노드, 그리고 값 자체가 있으므로 노드 클래스는 다음과 같습니다.class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}class Tree{
constructor(param = null) {
if (param) {
this.root = new Node(param);
} else {
this.root = null;
}
}
}object의 트리입니다.
왼쪽 하위 트리가 노드보다 작고 오른쪽 하위 트리가 노드보다 크다는 이진 검색 트리의 특성을 기반으로 새로운 이진 검색 트리 알고리즘을 다음과 같이 쉽게 작성할 수 있습니다.insert(key) {
if (this.root === null) {
this.root = new Node(key);
} else {
this._insertNode(this.root, key);
}
}
_insertNode(node, key) {
if (key < node.key) {
if (node.left === null) {
node.left = new Node(key);{1}
} else {
this._insertNode(node.left, key);{2}
}
} else if (key > node.key) {
if (node.right === null) {
node.right = new Node(key);{3}
} else {
this._insertNode(node.right, key);{4}
}
}
}JavaScript 함수가 값으로 전달되고, 매개변수가 기본이 아닌 유형인 경우, 여기의 객체로서 그 객체의 값은 메모리이므로 this.root의 내용은 매번 직접 변경됩니다.
이진 검색 트리 순회
이진 검색 트리는 선순(preorder), 중순(inorder), 후순(postorder)의 세 가지 순회 방법으로 나뉩니다.rreee
위의 순서는 순회입니다. 여기서 이해해야 할 것은 재귀입니다. 아시다시피 함수 실행은 데이터 구조, 즉 스택으로 추상화될 수 있습니다. 함수 실행을 위해 함수 실행을 저장하기 위해 스택이 유지됩니다. 함수가 반복될 때마다 현재 실행 환경을 스택에 푸시하고 실행 위치를 기록합니다. 위 코드를 예로 들면 다음과 같은 데이터가 있습니다 11부터 시작하여 스택에 대해 {1}을 실행한 다음 7로 이동하고 스택에 {1}을 실행한 다음 5로 이동하고 스택에 {1}을 실행한 다음 3으로 이동하여 {1을 실행합니다. }를 스택에 추가하는데 이때 노드 3의 왼쪽 자식 노드가 null인 것으로 확인되어 스택에서 튀어나오기 시작합니다. 이때 노드 3의 실행 환경이 팝업되어 {2}를 실행합니다. {3}, 3의 오른쪽 하위 노드도 null이고 {3}의 재귀 실행이 완료된 것을 확인한 다음 노드 5를 팝업하고 {2}{3}을 실행한 다음 노드 7을 팝업하고 실행합니다. {2}{3}을 스택에 추가하고 {3}을 실행할 때 노드 7에 올바른 노드가 있는 것으로 확인되었으므로 {1}을 계속 실행하고 노드 8에 대해 {1}을 다시 실행합니다. 8에는 왼쪽 자식이 없습니다. 노드, {1}이 실행되고, {2}{3}이 실행되는 식입니다. preorder와 midorder의 차이점은 노드 자체를 먼저 방문한다는 것, 즉 코드의 실행 순서가 2 1 3이라는 점입니다. 사후 주문에도 동일하게 적용되며 실행 순서는 1 3 2입니다. 순서가 이전, 도중, 이후에 관계없이 항상 왼쪽 노드가 먼저 재귀된다는 것을 찾는 것은 어렵지 않습니다. 왼쪽 노드를 순회하면 스택이 팝되고 모든 노드가 순회됩니다. 이들 사이의 유일한 차이점은 노드 자체에 액세스하는 타이밍입니다.이진 검색 트리 검색
검색은 매우 간단합니다. 왼쪽 자식 노드가 노드보다 작고 오른쪽 자식 노드가 노드보다 크다는 원칙에 따라 루프 판단을 내리면 됩니다.rreee
삭제는 더 복잡하며 다양한 상황에 따라 판단해야 합니다 먼저 노드에 왼쪽 하위 트리가 있는지 확인합니다. 왼쪽 하위 트리가 없으면 삭제된 노드를 오른쪽 하위 트리의 루트 노드로 직접 바꿉니다. 있는 경우 삭제된 노드를 오른쪽 하위 트리의 가장 작은 노드로 바꿉니다.remove(key) {
this._removeNode(this.root, key);
}
_removeNode(node, value) {
if (!node) {
return null;
}
if (value > node.key) {
node.right = this._removeNode(node.right, value);
} else if (value < node.key) {
node.left = this._removeNode(node.left, value);
} else {
// 如果没有左子树,那么将右子树根节点作为替换节点
if (!node.left) {
return node.right;
// 如果存在左子树,那么取右子树最小节点作为替换节点
} else if (node.left) {
return this._minNode(node.right);
}
}
}总结
总的来说,通过这次简单的二叉搜索树的学习,让我重新认识了递归,以前对于递归的理解只是一些简单的理论概念,这次深入实践让我对递归的理解又加深了许多。
这让我想到了数学的学习,数学的理论公式是很容易记住掌握的,如果说对一个知识点的掌握满分是十分,那么直到真正去实践它之前,只看公式的掌握只能是2分,因为公式很简单,就几句话几个原则,但是遇到的问题是千变万化的,只有真正将理论付诸实践,经过各种实践的打磨蹂躏,才能真正理解它其中的奥秘。
相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
위 내용은 JS 이진 검색 트리 사용에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7615
7615
 15
15
 1387
1387
 52
52
 88
88
 11
11
 68
68
 19
19
 29
29
 136
136
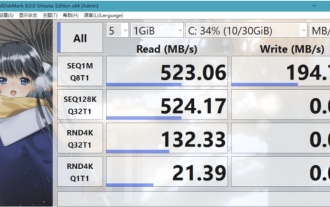 크리스탈디스크마크란 어떤 소프트웨어인가요? -크리스탈디스크마크는 어떻게 사용하나요?
Mar 18, 2024 pm 02:58 PM
크리스탈디스크마크란 어떤 소프트웨어인가요? -크리스탈디스크마크는 어떻게 사용하나요?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark는 순차 및 무작위 읽기/쓰기 속도를 빠르게 측정하는 하드 드라이브용 소형 HDD 벤치마크 도구입니다. 다음으로 편집자님에게 CrystalDiskMark 소개와 crystaldiskmark 사용법을 소개하겠습니다~ 1. CrystalDiskMark 소개 CrystalDiskMark는 기계식 하드 드라이브와 솔리드 스테이트 드라이브(SSD)의 읽기 및 쓰기 속도와 성능을 평가하는 데 널리 사용되는 디스크 성능 테스트 도구입니다. ). 무작위 I/O 성능. 무료 Windows 응용 프로그램이며 사용자 친화적인 인터페이스와 다양한 테스트 모드를 제공하여 하드 드라이브 성능의 다양한 측면을 평가하고 하드웨어 검토에 널리 사용됩니다.
 foobar2000을 어떻게 다운로드하나요? - foobar2000 사용법
Mar 18, 2024 am 10:58 AM
foobar2000을 어떻게 다운로드하나요? - foobar2000 사용법
Mar 18, 2024 am 10:58 AM
foobar2000은 언제든지 음악 리소스를 들을 수 있는 소프트웨어입니다. 모든 종류의 음악을 무손실 음질로 제공합니다. 음악 플레이어의 향상된 버전을 사용하면 더욱 포괄적이고 편안한 음악 경험을 얻을 수 있습니다. 컴퓨터에서 고급 오디오를 재생합니다. 이 장치는 보다 편리하고 효율적인 음악 재생 경험을 제공합니다. 인터페이스 디자인은 단순하고 명확하며 사용하기 쉽습니다. 또한 다양한 스킨과 테마를 지원하고, 자신의 선호도에 따라 설정을 개인화하며, 다양한 오디오 형식의 재생을 지원하는 전용 음악 플레이어를 생성합니다. 또한 볼륨을 조정하는 오디오 게인 기능도 지원합니다. 과도한 볼륨으로 인한 청력 손상을 방지하려면 자신의 청력 상태에 따라 조정하십시오. 다음엔 내가 도와줄게
 NetEase 메일박스 마스터를 사용하는 방법
Mar 27, 2024 pm 05:32 PM
NetEase 메일박스 마스터를 사용하는 방법
Mar 27, 2024 pm 05:32 PM
NetEase Mailbox는 중국 네티즌들이 널리 사용하는 이메일 주소로, 안정적이고 효율적인 서비스로 항상 사용자들의 신뢰를 얻어 왔습니다. NetEase Mailbox Master는 휴대폰 사용자를 위해 특별히 제작된 이메일 소프트웨어로 이메일 보내기 및 받기 프로세스를 크게 단순화하고 이메일 처리를 더욱 편리하게 만듭니다. 따라서 NetEase Mailbox Master를 사용하는 방법과 그 기능이 무엇인지 아래에서 이 사이트의 편집자가 자세한 소개를 제공하여 도움을 드릴 것입니다! 먼저, 모바일 앱스토어에서 NetEase Mailbox Master 앱을 검색하여 다운로드하실 수 있습니다. App Store 또는 Baidu Mobile Assistant에서 "NetEase Mailbox Master"를 검색한 후 안내에 따라 설치하세요. 다운로드 및 설치가 완료되면 NetEase 이메일 계정을 열고 로그인합니다. 로그인 인터페이스는 아래와 같습니다.
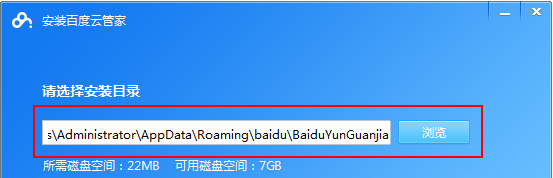 Baidu Netdisk 앱 사용 방법
Mar 27, 2024 pm 06:46 PM
Baidu Netdisk 앱 사용 방법
Mar 27, 2024 pm 06:46 PM
오늘날 클라우드 스토리지는 우리의 일상 생활과 업무에 없어서는 안 될 부분이 되었습니다. 중국 최고의 클라우드 스토리지 서비스 중 하나인 Baidu Netdisk는 강력한 스토리지 기능, 효율적인 전송 속도 및 편리한 운영 경험으로 많은 사용자의 호감을 얻었습니다. 중요한 파일을 백업하고, 정보를 공유하고, 온라인으로 비디오를 시청하고, 음악을 듣고 싶은 경우 Baidu Cloud Disk는 귀하의 요구를 충족할 수 있습니다. 그러나 많은 사용자가 Baidu Netdisk 앱의 구체적인 사용 방법을 이해하지 못할 수 있으므로 이 튜토리얼에서는 Baidu Netdisk 앱 사용 방법을 자세히 소개합니다. Baidu 클라우드 네트워크 디스크 사용 방법: 1. 설치 먼저 Baidu Cloud 소프트웨어를 다운로드하고 설치할 때 사용자 정의 설치 옵션을 선택하십시오.
 Win11에서 관리자 권한을 얻는 방법에 대한 자세한 설명
Mar 08, 2024 pm 03:06 PM
Win11에서 관리자 권한을 얻는 방법에 대한 자세한 설명
Mar 08, 2024 pm 03:06 PM
Windows 운영 체제는 세계에서 가장 인기 있는 운영 체제 중 하나이며, 새로운 버전의 Win11이 많은 주목을 받았습니다. Win11 시스템에서 관리자 권한을 얻는 것은 사용자가 시스템에서 더 많은 작업과 설정을 수행할 수 있도록 하는 중요한 작업입니다. 이번 글에서는 Win11 시스템에서 관리자 권한을 얻는 방법과 권한을 효과적으로 관리하는 방법을 자세히 소개하겠습니다. Win11 시스템에서 관리자 권한은 로컬 관리자와 도메인 관리자의 두 가지 유형으로 나뉩니다. 로컬 관리자는 로컬 컴퓨터에 대한 모든 관리 권한을 갖습니다.
 BTCC 튜토리얼: BTCC 교환에서 MetaMask 지갑을 바인딩하고 사용하는 방법은 무엇입니까?
Apr 26, 2024 am 09:40 AM
BTCC 튜토리얼: BTCC 교환에서 MetaMask 지갑을 바인딩하고 사용하는 방법은 무엇입니까?
Apr 26, 2024 am 09:40 AM
MetaMask(중국어로 Little Fox Wallet이라고도 함)는 무료이며 호평을 받는 암호화 지갑 소프트웨어입니다. 현재 BTCC는 MetaMask 지갑에 대한 바인딩을 지원합니다. 바인딩 후 MetaMask 지갑을 사용하여 빠르게 로그인하고 가치를 저장하고 코인을 구매할 수 있으며 첫 바인딩에는 20 USDT 평가판 보너스도 받을 수 있습니다. BTCCMetaMask 지갑 튜토리얼에서는 MetaMask 등록 및 사용 방법, BTCC에서 Little Fox 지갑을 바인딩하고 사용하는 방법을 자세히 소개합니다. MetaMask 지갑이란 무엇입니까? 3천만 명 이상의 사용자를 보유한 MetaMask Little Fox Wallet은 오늘날 가장 인기 있는 암호화폐 지갑 중 하나입니다. 무료로 사용할 수 있으며 확장으로 네트워크에 설치할 수 있습니다.
 Oracle SQL의 나누기 연산에 대한 자세한 설명
Mar 10, 2024 am 09:51 AM
Oracle SQL의 나누기 연산에 대한 자세한 설명
Mar 10, 2024 am 09:51 AM
OracleSQL의 나눗셈 연산에 대한 자세한 설명 OracleSQL에서 나눗셈 연산은 두 숫자를 나눈 결과를 계산하는 데 사용되는 일반적이고 중요한 수학 연산입니다. 나누기는 데이터베이스 쿼리에 자주 사용되므로 OracleSQL에서 나누기 작업과 사용법을 이해하는 것은 데이터베이스 개발자에게 필수적인 기술 중 하나입니다. 이 기사에서는 OracleSQL의 나누기 작업 관련 지식을 자세히 설명하고 독자가 참고할 수 있는 특정 코드 예제를 제공합니다. 1. OracleSQL의 Division 연산
 iOS 17.4 '도난 기기 보호'의 새로운 고급 기능을 사용하는 방법을 가르쳐주세요.
Mar 10, 2024 pm 04:34 PM
iOS 17.4 '도난 기기 보호'의 새로운 고급 기능을 사용하는 방법을 가르쳐주세요.
Mar 10, 2024 pm 04:34 PM
Apple은 화요일에 iOS 17.4 업데이트를 출시하여 iPhone에 수많은 새로운 기능과 수정 사항을 추가했습니다. 업데이트에는 새로운 이모티콘이 포함되어 있으며 EU 사용자는 다른 앱 스토어에서도 해당 이모티콘을 다운로드할 수 있습니다. 또한, 업데이트는 iPhone 보안 제어를 강화하고 사용자에게 더 많은 선택권과 보호 기능을 제공하기 위해 더 많은 "도난당한 장치 보호" 설정 옵션을 도입합니다. "iOS17.3에서는 최초로 '도난 기기 보호' 기능을 도입해 사용자의 민감한 정보에 대한 보안을 강화했습니다. 사용자가 집이나 기타 친숙한 장소를 떠나 있을 때 이 기능을 사용하려면 먼저 생체 정보를 입력해야 합니다. Apple ID 암호 변경, 도난 기기 보호 끄기 등 특정 데이터에 접근하고 변경하려면 정보를 다시 입력해야 합니다.




