TensorFlow가 무작위 훈련과 배치 훈련을 구현하는 방법
이 글에서는 주로 TensorFlow가 Random Training과 Batch Training을 구현하는 방법을 소개합니다. 이제 이를 공유하고 참고용으로 제공합니다. 와서 함께 살펴보세요
TensorFlow는 모델 변수를 업데이트합니다. 한 번에 하나의 데이터 포인트에서 작동하거나 한 번에 많은 양의 데이터에서 작동할 수 있습니다. 단일 훈련 예제로 작업하면 "기발한" 학습 프로세스가 발생할 수 있지만 대규모 배치를 사용한 훈련은 계산 비용이 많이 들 수 있습니다. 어떤 유형의 훈련을 선택하느냐는 기계 학습 알고리즘의 융합에 매우 중요합니다.
TensorFlow가 역전파가 작동하도록 가변 기울기를 계산하려면 하나 이상의 샘플에서 손실을 측정해야 합니다.
Random 훈련은 훈련 데이터와 목표 데이터 쌍을 무작위로 샘플링하여 훈련을 완료합니다. 또 다른 옵션은 대규모 배치 훈련에서 기울기 계산을 위한 손실을 평균화하는 것이며, 배치 훈련 크기를 전체 데이터 세트로 한 번에 확장할 수 있습니다. 여기서는 무작위 훈련과 배치 훈련을 사용하여 회귀 알고리즘의 이전 예를 확장하는 방법을 보여줍니다.
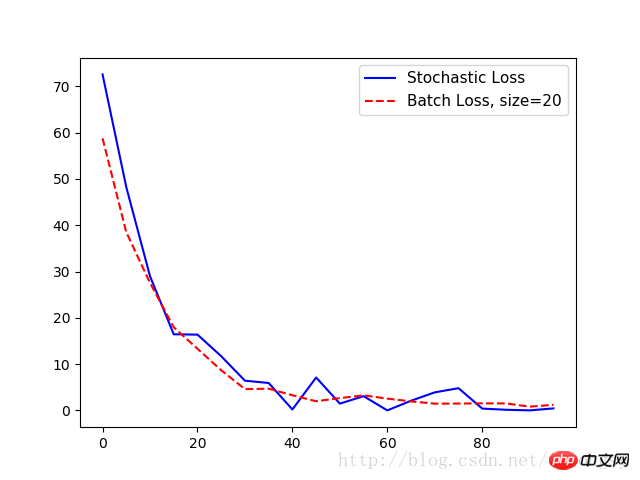
배치 훈련과 무작위 훈련의 차이점은 최적화 방법과 수렴입니다.
# 随机训练和批量训练
#----------------------------------
#
# This python function illustrates two different training methods:
# batch and stochastic training. For each model, we will use
# a regression model that predicts one model variable.
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
# 随机训练:
# Create graph
sess = tf.Session()
# 声明数据
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[1], dtype=tf.float32)
y_target = tf.placeholder(shape=[1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1]))
# 增加操作到图
my_output = tf.multiply(x_data, A)
# 增加L2损失函数
loss = tf.square(my_output - y_target)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_stochastic = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100)
rand_x = [x_vals[rand_index]]
rand_y = [y_vals[rand_index]]
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_stochastic.append(temp_loss)
# 批量训练:
# 重置计算图
ops.reset_default_graph()
sess = tf.Session()
# 声明批量大小
# 批量大小是指通过计算图一次传入多少训练数据
batch_size = 20
# 声明模型的数据、占位符
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1,1]))
# 增加矩阵乘法操作(矩阵乘法不满足交换律)
my_output = tf.matmul(x_data, A)
# 增加损失函数
# 批量训练时损失函数是每个数据点L2损失的平均值
loss = tf.reduce_mean(tf.square(my_output - y_target))
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_batch = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100, size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_batch.append(temp_loss)
plt.plot(range(0, 100, 5), loss_stochastic, 'b-', label='Stochastic Loss')
plt.plot(range(0, 100, 5), loss_batch, 'r--', label='Batch Loss, size=20')
plt.legend(loc='upper right', prop={'size': 11})
plt.show()출력:
단계 #5 A = [ 1.47604525]
손실 = [ 72.55678558]
단계 #10 A = [ 3.01128507]
손실 = [ 48.229 86221]
15단계 A = [4.27042341 ]
손실 = [ 28.97912598]
단계 #20 A = [ 5.2984333]
손실 = [ 16.44779968]
단계 #25 A = [ 6.17473984]
손실 = [ 16.373312]
단계 #30 A = [ 6 .89866304]
손실 = [ 11.71054649 ]
단계 #35 A = [ 7.39849901]
손실 = [ 6.42773056]
단계 #40 A = [ 7.84618378]
손실 = [ 5.92940331]
단계 #45 A = [ 8.15709 782]
손실 = [ 0 .2142024 ]
단계 #50 A = [ 8.54818344]
손실 = [ 7.11651039]
단계 #55 A = [ 8.82354641]
손실 = [ 1.47823763]
단계 #60 A = [ 9.07896614]
손실 = [ 3.08244276 ]
65단계 A = [ 9.24868107]
손실 = [ 0.01143846]
단계 #70 A = [ 9.36772251]
손실 = [ 2.10078788]
단계 #75 A = [ 9.49171734]
손실 = [ 3.9091370 1]
단계 #80 A = [ 9 . 6622715]
손실 = [ 4.80727625 ]
단계 #85 A = [ 9.73786926]
손실 = [ 0.39915398]
단계 #90 A = [ 9.81853104]
손실 = [ 0.14876099]
95단계 A = [ 9.90371323]
손실 = [ 0 .01657014]
단계 #100 A = [ 9.86669159]
손실 = [ 0.444787]
단계 #5 A = [[ 2.34371352]]
손실 = 58.766
단계 #10 A = [[ 3.74766445]]
손실 = 38.4875
15단계 A = [[ 4.88928795 ]]
손실 = 27.5632
20단계 A = [[ 5.82038736]]
손실 = 17.9523
25단계 A = [[ 6.58999157]]
손실 = 13.32 45
30단계 A = [[ 7.20851326 ]]
손실 = 8.68099
단계 #35 A = [[ 7.71694899]]
손실 = 4.60659
단계 #40 A = [[ 8.1296711]]
손실 = 4.70107
단계 #45 = [[ 8.47107315] ]
손실 = 3.28318
단계 #50 A = [[ 8.74283409]]
손실 = 1.99057
단계 #55 A = [[ 8.98811722]]
손실 = 2.66906
단계 #60 A = [[ 9.18062305 ]]
손실 = 3.26207
단계 #65 A = [[ 9.31655025 ]]
손실 = 2.55459
단계 #70 A = [[ 9.43130589]]
손실 = 1.95839
단계 #75 A = [[ 9.55670166]]
손실 = 1.465 04
스텝 #80A = [[ 9.6354847] ]
손실 = 1.49021
단계 #85 A = [[ 9.73470974]]
손실 = 1.53289
단계 #90 A = [[ 9.77956581]]
손실 = 1.52173
단계 #95 = [[ 9.83666706] ]
손실 = 0.819207
단계 #100 A = [[ 9.85569191]]
손실 = 1.2197
| 훈련 유형 | 장점 | 단점 |
|---|---|---|
| 무작위 훈련 | 로컬 최소값을 벗어남 | 일반적으로 업데이트 필요 수렴하려면 여러 번의 반복이 필요함 |
| 배치 훈련 | 최소 손실을 빠르게 확보 | 더 많은 컴퓨팅 리소스 소비 |
관련 권장 사항:
A tensorflow1.0 풀링 계층(풀링) 및 전체 연결 계층(고밀도)에 대한 간략한 이야기
Tensorflow 모델 저장 및 복원에 대한 간략한 토론
위 내용은 TensorFlow가 무작위 훈련과 배치 훈련을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7561
7561
 15
15
 1384
1384
 52
52
 84
84
 11
11
 60
60
 19
19
 28
28
 98
98
 오픈 소스! ZoeDepth를 넘어! DepthFM: 빠르고 정확한 단안 깊이 추정!
Apr 03, 2024 pm 12:04 PM
오픈 소스! ZoeDepth를 넘어! DepthFM: 빠르고 정확한 단안 깊이 추정!
Apr 03, 2024 pm 12:04 PM
0. 이 글은 어떤 내용을 담고 있나요? 우리는 다재다능하고 빠른 최첨단 생성 단안 깊이 추정 모델인 DepthFM을 제안합니다. DepthFM은 전통적인 깊이 추정 작업 외에도 깊이 인페인팅과 같은 다운스트림 작업에서 최첨단 기능을 보여줍니다. DepthFM은 효율적이며 몇 가지 추론 단계 내에서 깊이 맵을 합성할 수 있습니다. 이 작품을 함께 읽어보아요~ 1. 논문 정보 제목: DepthFM: FastMoncularDepthEstimationwithFlowMatching 저자: MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 인코더-디코더 아키텍처를 버리고 더 나은 결과를 얻기 위해 확산 모델을 사용하여 더 나은 결과를 얻었습니다.
Feb 07, 2024 pm 10:12 PM
인코더-디코더 아키텍처를 버리고 더 나은 결과를 얻기 위해 확산 모델을 사용하여 더 나은 결과를 얻었습니다.
Feb 07, 2024 pm 10:12 PM
현재 딥 에지 감지 네트워크는 일반적으로 다중 레벨 기능을 더 잘 추출하기 위해 업 및 다운 샘플링 모듈을 포함하는 인코더-디코더 아키텍처를 채택합니다. 그러나 이 구조는 정확하고 상세한 에지 감지 결과를 출력하기 위해 네트워크를 제한합니다. 이 문제에 대한 대응으로 AAAI2024에 대한 논문이 새로운 솔루션을 제공합니다. 논문 제목: DiffusionEdge:DiffusionProbabilisticModelforCrispEdgeDetection 저자: Ye Yunfan(국방기술대학교), Xu Kai(국립국방기술대학교), Huang Yuxing(국립국방기술대학교), Yi Renjiao(국립국방기술대학교), Cai Zhiping (국방기술대학교) 논문링크 : https://ar
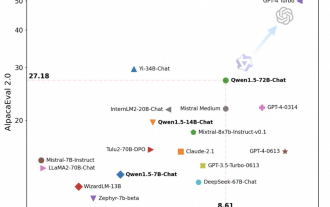 Tongyi Qianwen은 다시 오픈 소스이며 Qwen1.5는 6개 볼륨 모델을 제공하며 성능은 GPT3.5를 초과합니다.
Feb 07, 2024 pm 10:15 PM
Tongyi Qianwen은 다시 오픈 소스이며 Qwen1.5는 6개 볼륨 모델을 제공하며 성능은 GPT3.5를 초과합니다.
Feb 07, 2024 pm 10:15 PM
봄 축제에 맞춰 Tongyi Qianwen Large Model(Qwen) 버전 1.5가 온라인에 출시되었습니다. 오늘 아침, 새 버전 소식이 AI 커뮤니티의 이목을 끌었습니다. 대형 모델의 새 버전에는 0.5B, 1.8B, 4B, 7B, 14B 및 72B의 6가지 모델 크기가 포함됩니다. 그 중 가장 강력한 버전의 성능은 GPT3.5와 Mistral-Medium을 능가합니다. 이 버전에는 기본 모델과 채팅 모델이 포함되어 있으며 다국어 지원을 제공합니다. Alibaba의 Tongyi Qianwen 팀은 관련 기술이 Tongyi Qianwen 공식 웹사이트와 Tongyi Qianwen 앱에도 출시되었다고 밝혔습니다. 또한 오늘의 Qwen 1.5 릴리스에는 다음과 같은 주요 기능이 있습니다. 32K 컨텍스트 길이를 지원하고 Base+Chat 모델의 체크포인트를 엽니다.
 대형 모델도 슬라이스할 수 있으며 Microsoft SliceGPT는 LLAMA-2의 계산 효율성을 크게 높입니다.
Jan 31, 2024 am 11:39 AM
대형 모델도 슬라이스할 수 있으며 Microsoft SliceGPT는 LLAMA-2의 계산 효율성을 크게 높입니다.
Jan 31, 2024 am 11:39 AM
LLM(대형 언어 모델)은 일반적으로 수십억 개의 매개변수를 가지며 수조 개의 토큰에 대해 훈련됩니다. 그러나 이러한 모델은 훈련하고 배포하는 데 비용이 매우 많이 듭니다. 계산 요구 사항을 줄이기 위해 다양한 모델 압축 기술이 종종 사용됩니다. 이러한 모델 압축 기술은 일반적으로 증류, 텐서 분해(낮은 순위 인수분해 포함), 가지치기 및 양자화의 네 가지 범주로 나눌 수 있습니다. 가지치기 방법은 한동안 사용되어 왔지만 성능을 유지하기 위해 가지치기 후 RFT(복구 미세 조정)가 필요한 경우가 많아 전체 프로세스에 비용이 많이 들고 확장이 어렵습니다. ETH Zurich와 Microsoft의 연구원들은 SliceGPT라는 이 문제에 대한 솔루션을 제안했습니다. 이 방법의 핵심 아이디어는 가중치 행렬에서 행과 열을 삭제하여 네트워크의 임베딩을 줄이는 것입니다.
 안녕하세요, 일렉트릭 아틀라스입니다! 보스턴 다이나믹스 로봇 부활, 180도 이상한 움직임에 겁먹은 머스크
Apr 18, 2024 pm 07:58 PM
안녕하세요, 일렉트릭 아틀라스입니다! 보스턴 다이나믹스 로봇 부활, 180도 이상한 움직임에 겁먹은 머스크
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas가 공식적으로 전기 로봇 시대에 돌입했습니다! 어제 유압식 Atlas가 역사의 무대에서 "눈물을 흘리며" 물러났습니다. 오늘 Boston Dynamics는 전기식 Atlas가 작동 중이라고 발표했습니다. 상업용 휴머노이드 로봇 분야에서는 보스턴 다이내믹스가 테슬라와 경쟁하겠다는 각오를 다진 것으로 보인다. 새 영상은 공개된 지 10시간 만에 이미 100만 명이 넘는 조회수를 기록했다. 옛 사람들은 떠나고 새로운 역할이 등장하는 것은 역사적 필연이다. 올해가 휴머노이드 로봇의 폭발적인 해라는 것은 의심의 여지가 없습니다. 네티즌들은 “로봇의 발전으로 올해 개막식도 인간처럼 생겼고, 자유도도 인간보다 훨씬 크다. 그런데 정말 공포영화가 아닌가?”라는 반응을 보였다. 영상 시작 부분에서 아틀라스는 바닥에 등을 대고 가만히 누워 있는 모습입니다. 다음은 입이 떡 벌어지는 내용이다
 Gemini Pro를 따라잡고 추론 및 OCR 기능을 향상시키는 LLaVA-1.6은 너무 강력합니다.
Feb 01, 2024 pm 04:51 PM
Gemini Pro를 따라잡고 추론 및 OCR 기능을 향상시키는 LLaVA-1.6은 너무 강력합니다.
Feb 01, 2024 pm 04:51 PM
지난해 4월 위스콘신대학교 매디슨캠퍼스, 마이크로소프트 리서치, 컬럼비아대학교 연구진이 공동으로 LLaVA(Large Language and Vision Assistant)를 출시했다. LLaVA는 작은 다중 모드 명령 데이터 세트로만 교육되었지만 일부 샘플에서는 GPT-4와 매우 유사한 추론 결과를 보여줍니다. 그런 다음 10월에 원래 LLaVA에 대한 간단한 수정을 통해 11개 벤치마크에서 SOTA를 업데이트한 LLaVA-1.5를 출시했습니다. 이 업그레이드의 결과는 매우 흥미롭고 다중 모드 AI 보조 분야에 새로운 혁신을 가져옵니다. 연구팀은 추론, OCR,
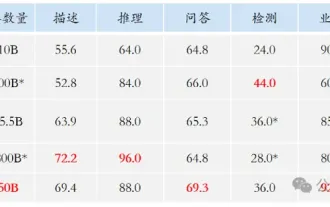 초지능의 생명력이 깨어난다! 하지만 자동 업데이트 AI가 등장하면서 엄마들은 더 이상 데이터 병목 현상을 걱정할 필요가 없습니다.
Apr 29, 2024 pm 06:55 PM
초지능의 생명력이 깨어난다! 하지만 자동 업데이트 AI가 등장하면서 엄마들은 더 이상 데이터 병목 현상을 걱정할 필요가 없습니다.
Apr 29, 2024 pm 06:55 PM
세상은 미친 듯이 큰 모델을 만들고 있습니다. 인터넷의 데이터만으로는 충분하지 않습니다. 훈련 모델은 '헝거게임'처럼 생겼고, 전 세계 AI 연구자들은 이러한 데이터를 탐식하는 사람들에게 어떻게 먹이를 줄지 고민하고 있습니다. 이 문제는 다중 모드 작업에서 특히 두드러집니다. 아무것도 할 수 없던 시기에, 중국 인민대학교 학과의 스타트업 팀은 자체 새로운 모델을 사용하여 중국 최초로 '모델 생성 데이터 피드 자체'를 현실화했습니다. 또한 이해 측면과 생성 측면의 두 가지 접근 방식으로 양측 모두 고품질의 다중 모드 새로운 데이터를 생성하고 모델 자체에 데이터 피드백을 제공할 수 있습니다. 모델이란 무엇입니까? Awaker 1.0은 중관촌 포럼에 최근 등장한 대형 멀티모달 모델입니다. 팀은 누구입니까? 소폰 엔진. 런민대학교 힐하우스 인공지능대학원 박사과정 학생인 Gao Yizhao가 설립했습니다.
 Sora 'Ke Ling'의 Kuaishou 버전이 테스트용으로 공개되었습니다. 120초가 넘는 비디오를 생성하고 물리학을 더 잘 이해하며 복잡한 움직임을 정확하게 모델링할 수 있습니다.
Jun 11, 2024 am 09:51 AM
Sora 'Ke Ling'의 Kuaishou 버전이 테스트용으로 공개되었습니다. 120초가 넘는 비디오를 생성하고 물리학을 더 잘 이해하며 복잡한 움직임을 정확하게 모델링할 수 있습니다.
Jun 11, 2024 am 09:51 AM
무엇? 주토피아는 국내 AI로 현실이 되는 걸까? 영상과 함께 노출된 것은 '켈링'이라는 국산 대형 영상세대 신형 모델이다. Sora는 유사한 기술 경로를 사용하고 자체 개발한 여러 기술 혁신을 결합하여 크고 합리적인 움직임뿐만 아니라 물리적 세계의 특성을 시뮬레이션하고 강력한 개념적 결합 능력과 상상력을 갖춘 비디오를 제작합니다. 데이터에 따르면 Keling은 최대 1080p의 해상도로 30fps에서 최대 2분의 초장 영상 생성을 지원하며 다양한 화면비를 지원합니다. 또 다른 중요한 점은 Keling이 실험실에서 공개한 데모나 비디오 결과 시연이 아니라 단편 비디오 분야의 선두주자인 Kuaishou가 출시한 제품 수준 애플리케이션이라는 점입니다. 더욱이 백지 작성이 아닌 실용성에 중점을 두고, 출시되자마자 온라인에 진출하는 데 중점을 두고 있다. 콰이잉에서는 커링의 대형 모델이 출시됐다.




