PHP는 정렬 힙 정렬 알고리즘을 구현합니다.
이 글은 주로 PHP에서 구현된 Heap Sort 알고리즘을 자세하게 소개하고 있으며, 관심 있는 친구들은 참고하시기 바랍니다.
#🎜🎜 #알고리즘 소개:# 🎜🎜# 여기서는 "Dahua 데이터 구조"의 시작 부분을 직접 인용합니다.
앞서 단순 선택 정렬에 대해 이야기했는데 정렬을 기다리고 있습니다. n개의 레코드 중에서 가장 작은 레코드를 선택하려면 다음이 필요합니다. n - 1번 비교. 이는 첫 번째 데이터를 찾아서 여러 번 비교해야 하는 것이 정상입니다. 그렇지 않으면 그것이 가장 작은 레코드인지 알 수 있습니다. 이 작업은 각 여행의 비교 결과를 저장하지 않습니다. 이전 여행에서 비교 결과가 더 무겁습니다. 한 번의 정렬 패스에서 저장되지 않았으므로 다음 정렬 패스에서 이러한 비교 작업이 반복되어 더 많은 수의 비교가 기록되었습니다. 매번 가장 작은 레코드를 선택하고 비교 결과에 따라 다른 레코드를 그에 맞게 조정할 수 있다면 전반적인 정렬 효율성이 매우 높아질 것입니다. 힙 정렬은 단순 선택 정렬을 개선한 것으로, 이러한 개선의 효과는 매우 분명합니다.기본 아이디어:
힙 정렬을 소개하기 전에 먼저 힙에 대해 소개하겠습니다.
《大话의 정의 데이터 구조: 힙은 다음 속성을 가진 완전한 이진 트리입니다. 각 노드의 값은 왼쪽 및 오른쪽 하위 노드의 값보다 크거나 같으며 큰 상단 힙(큰 루트 힙)이 됩니다. 각 노드의 왼쪽 및 오른쪽 노드의 값과 같거나 작으며 작은 최상위 힙(작은 루트 힙)이 됩니다. 이것을 보고 "힙이 완전한 이진 트리인지 아닌지"에 대한 의문도 생겼습니다. 힙은 완전한 이진 트리이므로 여전히 내 의견을 유보합니다. 여기서는 주로 저장과 계산을 용이하게 하기 위해 완전한 이진 트리 형태의 큰 루트 힙(작은 루트 힙)을 사용한다는 점만 알아야 합니다(편의성은 나중에 살펴보겠습니다).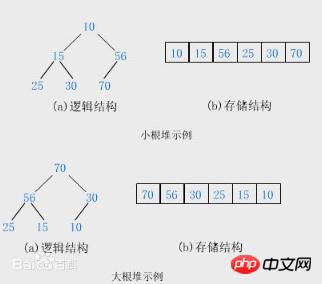 힙 정렬 알고리즘:
힙 정렬 알고리즘:
힙 정렬은 힙을 사용하는 것입니다( 큰 루트 힙 사용) 정렬 방법의 기본 아이디어는 정렬할 시퀀스를 큰 루트 힙으로 구성하는 것입니다. 이때 전체 시퀀스의 최대값은 힙 상단의 루트 노드이다. 이를 제거하고(실제로 이를 힙 배열의 마지막 요소와 교환합니다. 이때 마지막 요소는 최대값입니다.) 그런 다음 나머지 n - 1개 시퀀스를 힙으로 재구성하여 n 요소를 얻습니다. 다음으로 가장 작은 값입니다. 이것을 반복해서 실행하면 순서가 있는 시퀀스를 얻을 수 있습니다.
큰 루트 힙 정렬 알고리즘의 기본 작업: ①힙을 구축하는 것은 len/2부터 힙을 지속적으로 조정하는 과정입니다. 첫 번째 노드에 도달합니다. 여기서 len은 힙의 요소 수입니다. 힙을 만드는 과정은 선형 과정입니다. 힙을 조정하는 과정은 항상 len/2에서 0으로 호출됩니다. 이는 o(h1) + o(h2) ... + o(hlen/2)와 동일합니다. 여기서 h는 노드의 깊이를 나타내고, len/2는 노드의 수를 나타내며, 이는 합산 과정이며 결과는 선형 O(n)입니다. ②조정 힙: 조정 힙은 힙을 만드는 과정에서 사용되며, 힙 정렬 과정에서도 사용됩니다. 아이디어는 노드 i를 해당 하위 노드 left(i) 및 right(i)와 비교하고 세 개 중 가장 큰(또는 가장 작은) 값이 노드 i가 아니라 해당 하위 노드 중 하나인 경우를 선택하는 것입니다. , 거기에서 노드 i는 노드와 상호 작용한 다음 힙 조정 프로세스를 호출합니다. 이는 재귀 프로세스입니다. 힙을 조정하는 프로세스의 시간 복잡도는 힙의 깊이와 관련이 있습니다. 깊이 방향을 따라 조정되기 때문에 lgn의 작업입니다. 3힙 정렬: 위의 두 가지 과정을 통해 힙 정렬이 수행됩니다. 첫 번째는 요소를 기반으로 힙을 구축하는 것입니다. 그런 다음 힙의 루트 노드를 꺼내고(일반적으로 마지막 노드와 교환) 첫 번째 len-1 노드로 힙 조정 프로세스를 계속한 다음 모든 노드가 제거될 때까지 루트 노드를 제거합니다. 힙 정렬 프로세스의 시간 복잡도는 O(nlgn)입니다. 힙을 만드는 데 드는 시간 복잡도는 O(n)(1회 호출)이므로 힙을 조정하는 데 드는 시간 복잡도는 lgn이고 n-1번 호출되므로 힙 정렬의 시간 복잡도는 O(nlgn)입니다. 이 과정을 이해하려면 많은 다이어그램이 필요한데 게으릅니다. . . . . . 알고리즘 구현:<?php
//堆排序(对简单选择排序的改进)
function swap(array &$arr,$a,$b){
$temp = $arr[$a];
$arr[$a] = $arr[$b];
$arr[$b] = $temp;
}
//调整 $arr[$start]的关键字,使$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意这里节点 s 的左右孩子是 2*s + 1 和 2*s+2 (数组开始下标为 0 时)
function HeapAdjust(array &$arr,$start,$end){
$temp = $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算(我这里数组开始下标识 0)
//左孩子2 * $start + 1,右孩子2 * $start + 2
for($j = 2 * $start + 1;$j <= $end;$j = 2 * $j + 1){
if($j != $end && $arr[$j] < $arr[$j + 1]){
$j ++; //转化为右孩子
}
if($temp >= $arr[$j]){
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start] = $arr[$j];
//继续往下
$start = $j;
}
$arr[$start] = $temp;
}
function HeapSort(array &$arr){
$count = count($arr);
//先将数组构造成大根堆(由于是完全二叉树,所以这里用floor($count/2)-1,下标小于或等于这数的节点都是有孩子的节点)
for($i = floor($count / 2) - 1;$i >= 0;$i --){
HeapAdjust($arr,$i,$count);
}
for($i = $count - 1;$i >= 0;$i --){
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新树($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i - 1);
}
}
$arr = array(9,1,5,8,3,7,4,6,2);
HeapSort($arr);
var_dump($arr);시간 복잡도 분석:
# 🎜 🎜#실행 시간은 초기 빌드 쌍과 재구성 파일의 반복 심사에서만 소모됩니다. 전체적으로 힙 정렬의 시간 복잡도는 O(nlogn)입니다. 힙 정렬은 원본 레코드의 정렬 상태에 민감하지 않으므로 최고, 최악, 평균 시간 복잡도는 O(nlogn)입니다. 이는 버블링, 단순 선택 및 직접 삽입의 O(n^2) 시간 복잡도보다 성능 면에서 훨씬 더 좋습니다.
힙 정렬은 불안정한 정렬 방법입니다.
이 블로그는 "Dahua 데이터 구조"를 참조했습니다. 나중에 참고할 수 있도록 여기에만 기록되어 있습니다.
관심을 가질 만한 기사:
WeChat 점프 PHP 코드 구현에 대한 자세한 설명
WeChat의 Moments 공유 PHP 구현 설명 및 공유 횟수 기록 기능
위 내용은 PHP는 정렬 힙 정렬 알고리즘을 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 48
48
 19
19
 19
19
 20
20
 Ubuntu 및 Debian용 PHP 8.4 설치 및 업그레이드 가이드
Dec 24, 2024 pm 04:42 PM
Ubuntu 및 Debian용 PHP 8.4 설치 및 업그레이드 가이드
Dec 24, 2024 pm 04:42 PM
PHP 8.4는 상당한 양의 기능 중단 및 제거를 통해 몇 가지 새로운 기능, 보안 개선 및 성능 개선을 제공합니다. 이 가이드에서는 Ubuntu, Debian 또는 해당 파생 제품에서 PHP 8.4를 설치하거나 PHP 8.4로 업그레이드하는 방법을 설명합니다.
 CakePHP 토론
Sep 10, 2024 pm 05:28 PM
CakePHP 토론
Sep 10, 2024 pm 05:28 PM
CakePHP는 PHP용 오픈 소스 프레임워크입니다. 이는 애플리케이션을 훨씬 쉽게 개발, 배포 및 유지 관리할 수 있도록 하기 위한 것입니다. CakePHP는 강력하고 이해하기 쉬운 MVC와 유사한 아키텍처를 기반으로 합니다. 모델, 뷰 및 컨트롤러 gu
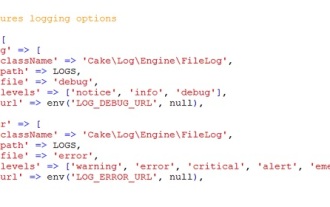 CakePHP 로깅
Sep 10, 2024 pm 05:26 PM
CakePHP 로깅
Sep 10, 2024 pm 05:26 PM
CakePHP에 로그인하는 것은 매우 쉬운 작업입니다. 한 가지 기능만 사용하면 됩니다. cronjob과 같은 백그라운드 프로세스에 대해 오류, 예외, 사용자 활동, 사용자가 취한 조치를 기록할 수 있습니다. CakePHP에 데이터를 기록하는 것은 쉽습니다. log() 함수는 다음과 같습니다.
 PHP 개발을 위해 Visual Studio Code(VS Code)를 설정하는 방법
Dec 20, 2024 am 11:31 AM
PHP 개발을 위해 Visual Studio Code(VS Code)를 설정하는 방법
Dec 20, 2024 am 11:31 AM
VS Code라고도 알려진 Visual Studio Code는 모든 주요 운영 체제에서 사용할 수 있는 무료 소스 코드 편집기 또는 통합 개발 환경(IDE)입니다. 다양한 프로그래밍 언어에 대한 대규모 확장 모음을 통해 VS Code는
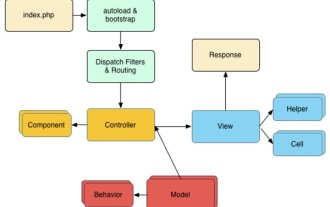 CakePHP 빠른 가이드
Sep 10, 2024 pm 05:27 PM
CakePHP 빠른 가이드
Sep 10, 2024 pm 05:27 PM
CakePHP는 오픈 소스 MVC 프레임워크입니다. 이를 통해 애플리케이션 개발, 배포 및 유지 관리가 훨씬 쉬워집니다. CakePHP에는 가장 일반적인 작업의 과부하를 줄이기 위한 여러 라이브러리가 있습니다.