JS는 힙 정렬을 구현합니다.

이 기사에서는 특정 참조 값을 갖는 JS 구현을 주로 소개합니다. 이제 모든 사람과 공유합니다. 필요한 친구가 참조할 수 있습니다.

힙에 대한 사전 지식

• 힙은 완전한 이진 트리입니다. .

• 완전 이진 트리: 이진 트리에서는 마지막 레이어를 제외하고 다른 레이어의 노드 수가 최대에 도달하고 마지막 레이어의 모든 노드가 왼쪽에 집중됩니다(노드가 누락될 수 있음). 왼쪽의 노드가 가득 찬 경우에만 오른쪽).

• 빅탑 힙: 루트 노드는 최대값이며, 각 노드의 값은 하위 노드의 값보다 크거나 같습니다.

• 작은 상단 힙: 루트 노드는 최소값이고, 각 노드의 값은 하위 노드의 값보다 작거나 같습니다.

• 힙 저장소: 힙은 배열로 구현되며 이는 이진 트리의 레벨 순서 순회와 동일합니다. 아래와 같이:

노드 i의 경우 하위 노드는 2i+1 및 2i+2입니다.

힙 정렬 알고리즘

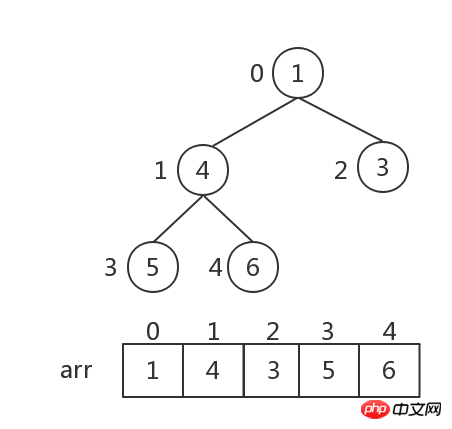
이제 위의 이진 트리를 오름차순으로 정렬해야 하며 이는 세 단계로 나뉩니다.

1. 초기 이진 트리를 큰 최상위 힙(힙파이)으로 변환합니다. 루트 노드가 최대값이 될 때 마지막 노드와 교환합니다.

2. 마지막 노드를 제외하고 나머지 노드로 구성된 새로운 힙을 큰 상위 힙으로 변환합니다. 이때 루트 노드는 하위 최대값이 되며 마지막 노드와 교환됩니다.

3. 힙의 요소 수가 1(또는 해당 배열의 길이가 1)이 될 때까지 2단계를 반복하고 정렬이 완료됩니다.

이 프로세스는 아래에 자세히 설명되어 있습니다.

1단계:

대형 최상위 힙을 초기화하고 먼저 리프가 아닌 마지막 노드를 선택합니다(상위 노드와 하위 노드 간의 크기 관계만 조정하면 됩니다). , 리프 노드 사이의 크기 관계는 조정할 필요가 없습니다. 배열이 arr이라고 가정하면 리프가 아닌 첫 번째 노드의 첨자는 다음과 같습니다. i = Math.floor(arr.length/2 - 1) = 1, 그림의 점선 상자에 표시된 대로 숫자 4입니다. , 세 개의 숫자를 찾으십시오. 최대 값은 상위 노드와 교환됩니다.

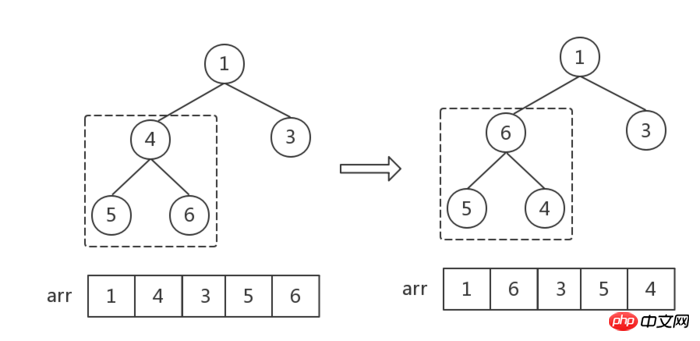
그런 다음 아래 첨자 i는 1씩 감소합니다(즉, 첫 번째 리프가 아닌 노드부터 시작하여 모든 리프가 아닌 노드를 오른쪽에서 왼쪽으로, 아래에서 위로 순회). 이후의 모든 조정은 동일합니다. 즉, 상위 노드와 하위 노드 사이에서 최대값을 찾아 교환합니다.

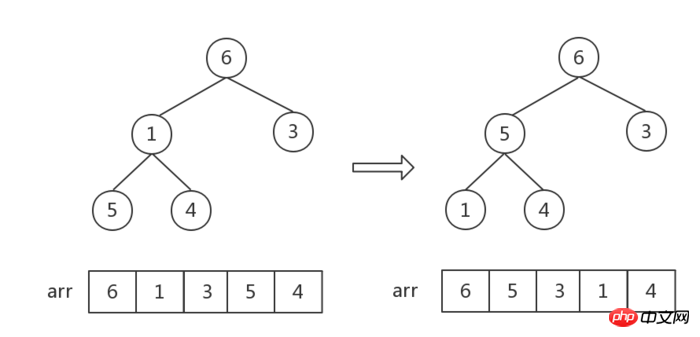
이 단계에서 숫자 6과 1이 바뀌고 나면 숫자 [1,5,4]로 구성된 힙의 순서가 잘못되어 한 단계 조정이 필요합니다. 따라서 리프가 아닌 노드를 조정할 때마다 하위 힙 순서에 영향을 미치는지 관찰해야 한다는 점에 유의하는 것이 중요합니다!

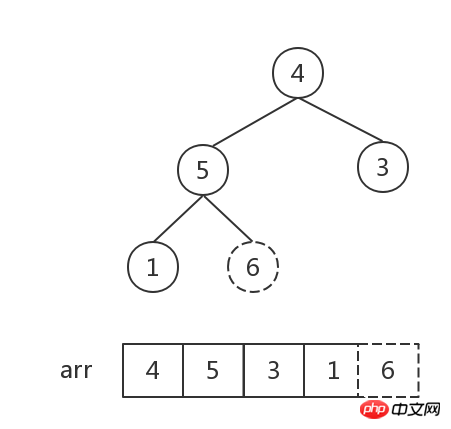
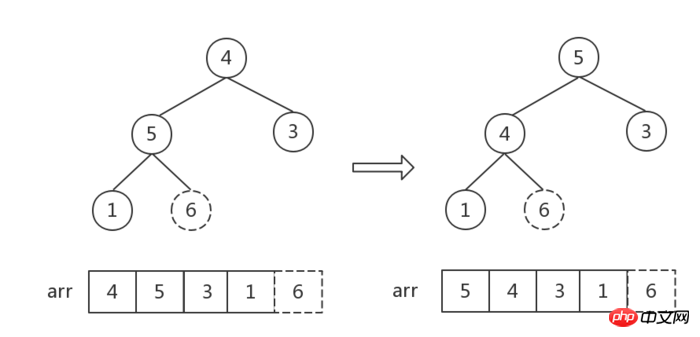
이 조정 후에는 루트 노드가 최대값이 되어 큰 최상위 힙을 형성하고 루트 노드가 마지막 노드와 교환됩니다.

2단계:

현재 마지막 노드 6(즉, 최대값)을 제외하고 나머지 노드 [4,5,3,1]의 새로운 힙을 형성하고 이를 큰 상위 힙으로 변환합니다(참고: 이번에는 루트 노드 이외의 다른 노드는 모두 큰 상위 힙의 특성을 충족하므로 루트 노드 4부터 조정을 시작할 수 있습니다. 즉, 4가 있어야 할 위치를 찾을 수 있습니다.

3단계:

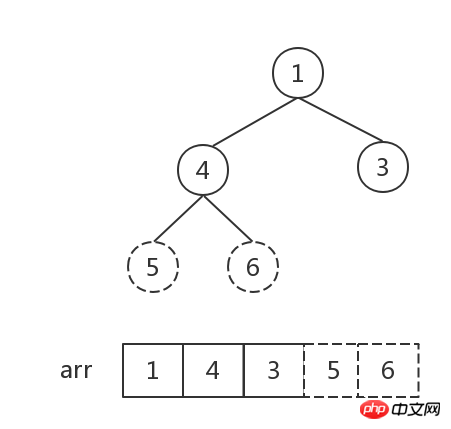
다음으로 힙의 요소 수가 1이 될 때까지 2단계를 반복합니다. 힙의 요소 수 은 1 이고 정렬이 완료되었습니다.

JavaScript 구현

// 交换两个节点
function swap(A, i, j) {
  let temp = A[i];
  A[i] = A[j];
  A[j] = temp; 
}

// 将 i 结点以下的堆整理为大顶堆，注意这一步实现的基础实际上是：
// 假设 结点 i 以下的子堆已经是一个大顶堆，adjustheap 函数实现的
// 功能是实际上是：找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环，从第一个非叶子结点开始，对每一个非叶子结点
// 都执行 adjustheap 操作，所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
  let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
    adjustHeap(A, i, A.length);
  }
  // 排序，每一次for循环找出一个当前最大值，数组长度减一
  for(let i = Math.floor(A.length-1); i>0; i--) {
    swap(A, 0, i); // 根节点与最后一个节点交换
    adjustHeap(A, 0, i); // 从根节点开始调整，并且最后一个结点已经为当
                         // 前最大值，不需要再参与比较，所以第三个参数
                         // 为 i，即比较到最后一个结点前一个即可
  }
}

let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>

프로그램 참고 사항: 노드 i 아래의 힙을 큰 상위 힙으로 구성합니다. 실제로 이 단계의 기본은 다음과 같습니다. 노드 i 아래의 하위 힙이 이미 큰 상위 힙이라고 가정하고 adjustHeap 함수 구현을 수행합니다. 실제로 함수는 노드 i를 포함하는 힙에서 노드 i의 올바른 위치를 찾는 것입니다. 나중에 첫 번째 힙을 수행할 때 heapSort에 for 루프가 작성됩니다. 첫 번째 리프가 아닌 노드부터 시작하여 각 리프가 아닌 노드에서 adjustHeap 작업이 수행되므로 각 adjustHeap에서 노드는 하위- i 아래의 힙은 이미 큰 최상위 힙입니다.

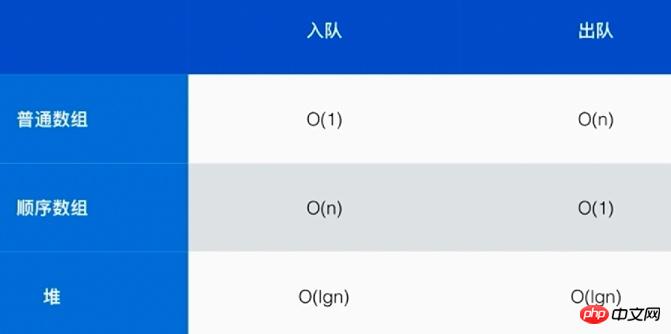
복잡도 분석: adjustHeap 함수는 힙의 레이어당 하나의 노드만 통과합니다. 왜냐하면 n 노드가 있는 완전한 이진 트리의 깊이는 [log2n]+1이므로 adjustHeap의 복잡도는 O(logn)이고 외부 루프의 총 횟수는 f(n)이므로 최종 복잡도는 O(nlogn)입니다.

힙의 응용

Heap은 주로 우선순위 대기열을 구현하는 데 사용됩니다. 다음은 우선순위 대기열의 적용 예입니다.

• 운영 체제는 실행 우선순위가 가장 높은 작업을 동적으로 선택합니다.

• 정적 문제에서 N개의 요소 중에서 상위 M개의 이름을 선택하는 경우 정렬 사용 복잡도: O(NlogN), 우선순위 큐 사용 복잡도: O(NlogM).

우선순위 큐를 구현하기 위해 일반 배열, 순차 배열 및 힙을 사용할 때의 다양한 복잡성은 다음과 같습니다.

힙을 사용하여 우선순위 큐를 구현하면 큐에 넣기와 큐에서 빼기의 복잡성이 매우 낮아질 수 있습니다.

위 내용은 이 글의 전체 내용입니다. 모든 분들의 학습에 도움이 되었으면 좋겠습니다. 더 많은 관련 내용은 PHP 중국어 홈페이지를 주목해주세요!

관련 권장 사항:

JS는 병합 정렬을 구현합니다

JS는 Hill 정렬을 구현합니다

위 내용은 JS는 힙 정렬을 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!