javascript_javascript 기술에서 일반적으로 사용되는 클래식 알고리즘 예제에 대한 자세한 설명

이 기사의 예에서는 JavaScript의 일반적인 알고리즘을 설명합니다. 참고하실 수 있도록 모든 사람과 공유하세요. 자세한 내용은 다음과 같습니다.

초급 알고리즘-선형 검색-시간 복잡도 O(n)--알고리즘 세계의 HelloWorld

와 동일

//线性搜索(入门HelloWorld)
//A为数组，x为要搜索的值
function linearSearch(A, x) {
  for (var i = 0; i < A.length; i++) {
    if (A[i] == x) {
      return i;
    }
  }
  return -1;
}

이진 검색(절반 검색이라고도 함) - 정렬된 선형 구조에 적합 - 시간 복잡도 O(logN)

//二分搜索
//A为已按"升序排列"的数组，x为要查询的元素
//返回目标元素的下标
function binarySearch(A, x) {
  var low = 0, high = A.length - 1;
  while (low <= high) {
    var mid = Math.floor((low + high) / 2); //下取整   
    if (x == A[mid]) {
      return mid;
    }
    if (x < A[mid]) {
      high = mid - 1;
    }
    else {
      low = mid + 1;
    }
  }
  return -1;
}

버블 정렬 -- 시간 복잡도 O(n^2)

//冒泡排序
function bubbleSort(A) {
  for (var i = 0; i < A.length; i++) {
    var sorted = true;
  //注意：内循环是倒着来的
    for (var j = A.length - 1; j > i; j--) {
      if (A[j] < A[j - 1]) {
        swap(A, j, j - 1);
        sorted = false;
      }
    }
    if (sorted) {
      return;
    }
  }
}

선택 정렬 -- 시간 복잡도 O(n^2)

//选择排序
//思路：找到最小值的下标记下来，再交换
function selectionSort(A) {
  for (var i = 0; i < A.length - 1; i++) {
    var k = i;
    for (var j = i + 1; j < A.length; j++) {
      if (A[j] < A[k]) {
        k = j;
      }
    }
    if (k != i) {
      var t = A[k];
      A[k] = A[i];
      A[i] = t;
      println(A);
    }
  }
  return A;
}

삽입 정렬 -- 시간 복잡도 O(n^2)

//插入排序
//假定当前元素之前的元素已经排好序，先把自己的位置空出来，
//然后前面比自己大的元素依次向后移，直到空出一个"坑"，
//然后把目标元素插入"坑"中
function insertSort(A) {
  for (var i = 1; i < A.length; i++) {
    var x = A[i];
    for (var j = i - 1; j >= 0 && A[j] > x; j--) {
      A[j + 1] = A[j];
    }
    if (A[j + 1] != x) {
      A[j + 1] = x;
      println(A);
    }
  }
  return A;
}

문자열 반전 -- 시간 복잡도 O(logN)

//字符串反转(比如：ABC -> CBA)
function inverse(s) {
  var arr = s.split('');
  var i = 0, j = arr.length - 1;
  while (i < j) {
    var t = arr[i];
    arr[i] = arr[j];
    arr[j] = t;
    i++;
    j--;
  }
  return arr.join('');
}

안정성 순위에 대한 결론:

비교 기반의 단순 정렬 ​​알고리즘, 즉 시간 복잡도가 O(N^2)인 정렬 알고리즘으로 일반적으로 안정적인 정렬이라고 볼 수 있습니다
병합 정렬, 힙 정렬, 버킷 정렬(일반적으로 이러한 알고리즘의 시간 복잡도는 n*LogN으로 최적화될 수 있음)과 같은 기타 고급 정렬 알고리즘은 일반적으로 불안정한 정렬로 간주될 수 있습니다.

단일 연결 목록구현

<script type="text/javascript">
  function print(msg) {
    document.write(msg);
  }
  function println(msg) {
    print(msg + "<br/>");
  }
  //节点类
  var Node = function (v) {
    this.data = v; //节点值
    this.next = null; //后继节点
  }
  //单链表
  var SingleLink = function () {
    this.head = new Node(null); //约定头节点仅占位，不存值
    //插入节点
    this.insert = function (v) {
      var p = this.head;
      while (p.next != null) {
        p = p.next;
      }
      p.next = new Node(v);
    }
    //删除指定位置的节点
    this.removeAt = function (n) {
      if (n <= 0) {
        return;
      }
      var preNode = this.getNodeByIndex(n - 1);
      preNode.next = preNode.next.next;
    }
    //取第N个位置的节点(约定头节点为第0个位置)
    //N大于链表元素个数时，返回最后一个元素
    this.getNodeByIndex = function (n) {
      var p = this.head;
      var i = 0;
      while (p.next != null && i < n) {
        p = p.next;
        i++;
      }
      return p;
    }
    //查询值为V的节点，
    //如果链表中有多个相同值的节点，
    //返回第一个找到的
    this.getNodeByValue = function (v) {
      var p = this.head;
      while (p.next != null) {
        p = p.next;
        if (p.data == v) {
          return p;
        }
      }
      return null;
    }
    //打印输出所有节点
    this.print = function () {
      var p = this.head;
      while (p.next != null) {
        p = p.next;
        print(p.data + " ");
      }
      println("");
    }
  }
  //测试单链表L中是否有重复元素
  function hasSameValueNode(singleLink) {
    var i = singleLink.head;
    while (i.next != null) {
      i = i.next;
      var j = i;
      while (j.next != null) {
        j = j.next;
        if (i.data == j.data) {
          return true;
        }
      }
    }
    return false;
  }
  //单链表元素反转
  function reverseSingleLink(singleLink) {
    var arr = new Array();
    var p = singleLink.head;
    //先跑一遍，把所有节点放入数组
    while (p.next != null) {
      p = p.next;
      arr.push(p.data);
    }
    var newLink = new SingleLink();
    //再从后向前遍历数组,加入新链表
    for (var i = arr.length - 1; i >= 0; i--) {
      newLink.insert(arr[i]);
    }
    return newLink;
  }
  var linkTest = new SingleLink();
  linkTest.insert('A');
  linkTest.insert('B');
  linkTest.insert('C');
  linkTest.insert('D');
  linkTest.print();//A B C D
  var newLink = reverseSingleLink(linkTest);
  newLink.print();//D C B A
</script>

인접 행렬 및 인접 목록 선택에 대해

:

인접 행렬과 인접 리스트는 그래프의 기본 저장 방식입니다. 희소 그래프의 경우
(즉, 모서리가 꼭짓점보다 훨씬 작은 경우) 인접 목록 저장을 사용하는 것이 더 적합합니다(행렬 N*N에 비해 인접 목록은 값이 있는 가장자리와 꼭지점을 사용하며 null 값을 저장하지 않습니다. 더 효율적인 저장) 밀집 그래프

(즉, 원격 정점의 경우)의 경우 인접 행렬로 저장하는 것이 더 적합합니다(데이터가 많을 경우 순회해야 함). 연결리스트를 사용하여 저장하면 자주 뛰어다녀야 하므로 효율성이 떨어집니다.

힙:

거의 완전한 이진 트리: 이진 트리

가장 오른쪽 위치에 하나 또는 여러 개의 리프가 누락될 수 있다는 점만 제외됩니다. 물리적 저장 측면에서 배열을 사용하여 A[j]의 정점에 왼쪽 및 오른쪽 자식 노드가 있는 경우 왼쪽 노드는 A[2j]이고 오른쪽 노드는 A[2j 1]입니다. A[j/2]

에 저장된 A[j]의 상위 정점 힙: 자체는 거의 완전한 이진 트리이며, 상위 노드의 값은 하위 노드

의 값보다 작지 않습니다. 응용 시나리오: 우선 순위 대기열, 최대 또는 하위 최대 값 찾기 및 우선 순위 대기열에 새 요소 삽입.

참고: 아래에 설명된 모든 힙에서는 인덱스 0의 요소만 발생하고 유효한 요소는 아래 첨자 1부터 시작하는 것으로 합의되었습니다.

힙의 정의에 따라 다음 코드를 사용하여 배열이 힙인지 테스트할 수 있습니다.

//测试数组H是否为堆
//(约定有效元素从下标1开始)
//时间复杂度O(n)
function isHeap(H) {
  if (H.length <= 1) { return false; }
  var half = Math.floor(H.length / 2); //根据堆的性质，循环上限只取一半就够了
  for (var i = 1; i <= half; i++) {
    //如果父节点，比任何一个子节点 小，即违反堆定义
    if (H[i] < H[2 * i] || H[i] < H[2 * i + 1]) {
      return false;
    }
  }
  return true;
}

노드 조정 선별

어떤 경우에는 힙에 있는 요소의 값이 변경되면(예: 10,8,9,7이 10,8,9,20이 된 후 20을 위쪽으로 조정해야 함) 더 이상 충족되지 않습니다. 힙의 정의를 상향 조정해야 하는 경우 다음 코드를 사용하여

를 달성할 수 있습니다.

//堆中的节点上移
//(约定有效元素从下标1开始)
function siftUp(H, i) {
  if (i <= 1) {
    return;
  }
  for (var j = i; j > 1; j = Math.floor(j / 2)) {
    var k = Math.floor(j / 2);
    //发现 子节点 比 父节点大，则与父节点交换位置
    if (H[j] > H[k]) {
      var t = H[j];
      H[j] = H[k];
      H[k] = t;
    }
    else {
      //说明已经符合堆定义，调整结束，退出
      return;
    }
  }
}

siftDown으로 노드를 하향 조정합니다(상향 조정이 있으니 당연히 하향 조정이 발생합니다)

//堆中的节点下移
//(约定有效元素从下标1开始)
//时间复杂度O(logN)
function siftDown(H, i) {
  if (2 * i > H.length) { //叶子节点，就不用再向下移了
    return;
  }
  for (var j = 2 * i; j < H.length; j = 2 * j) {
    //将j定位到 二个子节点中较大的那个上(很巧妙的做法)
    if (H[j + 1] > H[j]) {
      j++;
    }
    var k = Math.floor(j / 2);
    if (H[k] < H[j]) {
      var t = H[k];
      H[k] = H[j];
      H[j] = t;
    }
    else {
      return;
    }
  }
}

힙에 새 요소 추가

//向堆H中添加元素x
//时间复杂度O(logN)
function insert(H, x) {
  //思路：先在数组最后加入目标元素x
  H.push(x);
  //然后向上推
  siftUp(H, H.length - 1);
}

힙에서 요소 제거

//删除堆H中指定位置i的元素
//时间复杂度O(logN)
function remove(H, i) {
  //思路：先把位置i的元素与最后位置的元素n交换
  //然后数据长度减1(这样就把i位置的元素给干掉了，但是整个堆就被破坏了)
  //需要做一个决定：最后一个元素n需要向上调整，还是向下调整
  //依据：比如比原来该位置的元素大，则向上调整，反之向下调整
  var x = H[i]; //先把原来i位置的元素保护起来
  //把最后一个元素放到i位置
  //同时删除最后一个元素(js语言的优越性体现!)
  H[i] = H.pop();
  var n = H.length - 1;
  if (i == n + 1) {
    //如果去掉的正好是最后二个元素之一，
    //无需再调整
    return ;
  }
  if (H[i] > x) {
    siftUp(H, i);
  }
  else {
    siftDown(H, i);
  }
}
//从堆中删除最大项
//返回最大值
//时间复杂度O(logN)
function deleteMax(H) {
  var x = H[1];
  remove(H, 1);
  return x;
}

힙 정렬

:

이것은 매우 영리한 정렬 알고리즘의 핵심은 데이터 구조 "힙"(첫 번째 요소가 가장 커야 함)의 특성을 최대한 활용하는 데 있으며 각 요소는 시간 재테스트를 통해 위 또는 아래로 이동할 수 있습니다. 공간적으로는 상대적으로 낮으며, 추가 저장 공간이 필요하지 않고 배열 자체 내에서 요소를 교환하면 됩니다.

사물:

1. 먼저 첫 번째 요소(즉, 가장 큰 요소)를 마지막 요소로 바꿉니다. 목적은 최대값을 맨 아래로 가라앉히고 다음 라운드에서 무시하는 것입니다.
2. 1 이후 나머지 요소는 일반적으로 더 이상 힙이 아닙니다. 이때 siftDown을 사용하여 새로운 첫 번째 요소를 아래쪽으로 조정하면 새로운 최대 요소가 자연스럽게 첫 번째 요소의 위치로 올라갑니다
3. 1과 2를 반복하면 큰 요소들이 하나씩 아래쪽으로 가라앉고 마침내 전체 배열이 정리됩니다.

시간 복잡도 분석: 힙을 생성하려면 O(n) 비용이 필요하고 각 siftDown 비용은 O(logN)이며 최대 n-1개의 요소를 조정할 수 있으므로 총 비용은 O(N) (N-1)O( logN) , 최종 시간 복잡도는 O(NLogN)

//堆中的节点下移
//(约定有效元素从下标1开始)
//i为要调整的元素索引
//n为待处理的有效元素下标范围上限值
//时间复杂度O(logN)
function siftDown(H, i, n) {
  if (n >= H.length) {
    n = H.length;
  }
  if (2 * i > n) { //叶子节点，就不用再向下移了
    return;
  }
  for (var j = 2 * i; j < n; j = 2 * j) {
    //将j定位到 二个子节点中较大的那个上(很巧妙的做法)
    if (H[j + 1] > H[j]) {
      j++;
    }
    var k = Math.floor(j / 2);
    if (H[k] < H[j]) {
      var t = H[k];
      H[k] = H[j];
      H[j] = t;
    }
    else {
      return;
    }
  }
}
//对数组的前n个元素进行创建堆的操作
function makeHeap(A, n) {
  if (n >= A.length) {
    n = A.length;
  }
  for (var i = Math.floor(n / 2); i >= 1; i--) {
    siftDown(A, i, n);
  }
}
//堆排序(非降序排列)
//时间复杂度O(nlogN)
function heapSort(H) {
  //先建堆
  makeHeap(H, H.length);
  for (var j = H.length - 1; j >= 2; j--) {
    //首元素必然是最大的
    //将最大元素与最后一个元素互换，
    //即将最大元素沉底，下一轮不再考虑
    var x = H[1];
    H[1] = H[j];
    H[j] = x;
    //互换后，剩下的元素不再满足堆定义，
    //把新的首元素下调(以便继续维持堆的"形状")
    //调整完后，剩下元素中的最大值必须又浮到了第一位
    //进入下一轮循环
    siftDown(H, 1, j - 1);
  }
  return H;
}

힙을 쌓는 것에 관해서는 원리를 이해하면 아이디어를 거꾸로 해서도 할 수 있습니다

function makeHeap2(A, n) {
  if (n >= A.length) {
    n = A.length;
  }
  for (var i = Math.floor(n / 2); i <= n; i++) {
    siftUp(A, i);
  }
}

분리된 집합 검색 및 병합

//定义节点Node类
var Node = function (v, p) {
    this.value = v; //节点的值
    this.parent = p; //节点的父节点
    this.rank = 0; //节点的秩(默认为0)    
}
//查找包含节点x的树根节点 
var find = function (x) {
    var y = x;
    while (y.parent != null) {
      y = y.parent;
    }
    var root = y;
    y = x;
    //沿x到根进行“路径压缩”
    while (y.parent != null) {
      //先把父节点保存起来，否则下一行调整后，就弄丢了
      var w = y.parent;
      //将目标节点挂到根下
      y.parent = root;
      //再将工作指针，还原到 目标节点原来的父节点上，
      //继续向上逐层压缩
      y = w
    }
    return root;
}
//合并节点x，y对应的两个树
//时间复杂度O(m) - m为待合并的子集合数量
var union = function (x, y) {
    //先找到x所属集合的根
    var u = find(x);
    //再找到y所属集合的根
    var v = find(y);
    //把rank小的集合挂到rank大的集合上
    if (u.rank <= v.rank) {
      u.parent = v;
      if (u.rank == v.rank) {
        //二个集合的rank不分伯仲时
        //给"胜"出方一点奖励，rank+1
        v.rank += 1;
      }
    }
    else {
      v.parent = u;
    }
}

유도 방법

:

우선 정렬의 두 가지 재귀 구현을 살펴보겠습니다

//选择排序的递归实现
//调用示例: selectionSort([3,2,1],0)
function selectionSortRec(A, i) {
  var n = A.length - 1;
  if (i < n) {
    var k = i;
    for (var j = i + 1; j <= n; j++) {
      if (A[j] < A[k]) {
        k = j
      }
    }
    if (k != i) {
      var t = A[k];
      A[k] = A[i];
      A[i] = t;
    }
    selectionSortRec(A, i + 1);
  }
}
//插入排序递归实现
//调用示例:insertSortRec([4,3,2,1],3);
function insertSortRec(A, i) {
  if (i > 0) {
    var x = A[i];
    insertSortRec(A, i - 1);
    var j = i - 1;
    while (j >= 0 && A[j] > x) {
      A[j + 1] = A[j];
      j--;
    }
    A[j + 1] = x;
  }
}

재귀 프로그램은 일반적으로 이해하기 쉽고 코드도 구현하기 쉽습니다. 두 가지 작은 예를 살펴보겠습니다.

배열에서 최대값 찾기

//在数组中找最大值(递归实现)
function findMax(A, i) {
  if (i == 0) {
    return A[0];
  }
  var y = findMax(A, i - 1);
  var x = A[i - 1];
  return y > x ? y : x;
}
var A = [1,2,3,4,5,6,7,8,9];
var test = findMax(A,A.length);
alert(test);//返回9

오름차순으로 정렬된 배열이 있습니다. 배열에 두 개의 숫자가 있는지, 그 합이 정확히 x인지 확인하세요.

//5.33 递归实现
//A为[1..n]已经排好序的数组
//x为要测试的和
//如果存在二个数的和为x，则返回true，否则返回false
function sumX(A, i, j, x) {
  if (i >= j) {
    return false;
  }
  if (A[i] + A[j] == x) {
    return true;
  }
  else if (A[i] + A[j] < x) {
    //i后移
    return sumX(A, i + 1, j, x);
  }
  else {
    //j前移
    return sumX(A, i, j - 1, x);
  }
}
var A = [1, 2, 3, 4, 5, 6, 7, 8];
var test1 = sumX(A,0,A.length-1,9);
alert(test1); //返回true

<🎜>

递归程序虽然思路清晰，但通常效率不高，一般来讲，递归实现，都可以改写成非递归实现，上面的代码也可以写成：

//5.33 非递归实现
function sumX2(A, x) {
  var i = 0, j = A.length - 1;
  while (i < j) {
    if (A[i] + A[j] == x) {
      return true;
    }
    else if (A[i] + A[j] < x) {
      //i后移
      i++;
    }
    else {
      //j前移
      j--;
    }
  }
  return false;
}
var A = [1, 2, 3, 4, 5, 6, 7, 8];
var test2 = sumX2(A,9);
alert(test2);//返回true

递归并不总代表低效率，有些场景中，递归的效率反而更高，比如计算x的m次幂，常规算法，需要m次乘法运算，下面的算法，却将时间复杂度降到了O(logn)

//计算x的m次幂（递归实现）
//时间复杂度O(logn)
function expRec(x, m) {
  if (m == 0) {
    return 1;
  }
  var y = expRec(x, Math.floor(m / 2));
  y = y * y;
  if (m % 2 != 0) {
    y = x * y
  }
  return y;
}

当然，这其中并不光是递归的功劳，其效率的改进 主要依赖于一个数学常识： x^m = [x^(m/2)]^2，关于这个问题，还有一个思路很独特的非递归解法，巧妙的利用了二进制的特点

//将10进制数转化成2进制
function toBin(dec) {
  var bits = [];
  var dividend = dec;
  var remainder = 0;
  while (dividend >= 2) {
    remainder = dividend % 2;
    bits.push(remainder);
    dividend = (dividend - remainder) / 2;
  }
  bits.push(dividend);
  bits.reverse();
  return bits.join("");
}
//计算x的m次幂（非递归实现）
//很独特的一种解法
function exp(x, m) {
  var y = 1;
  var bin = toBin(m).split('');
  //先将m转化成2进制形式
  for (var j = 0; j < bin.length; j++) {
    y = y * 2;
    //如果2进制的第j位是1，则再*x
    if (bin[j] == "1") {
      y = x * y
    }
  }
  return y;
}
//println(expRec(2, 5));
//println(exp(2, 5));

再来看看经典的多项式求值问题：

给定一串实数An，An-1，...，A1，A0 和一个实数X，计算多项式Pn(x)的值

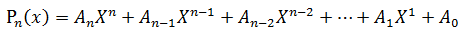
著名的Horner公式：

已经如何计算：

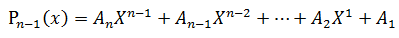
显然有：

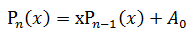
这样只需要 N次乘法+N次加法

//多项式求值
//N次乘法+N次加法搞定，伟大的改进！
function horner(A, x) {
  var n = A.length - 1
  var p = A[n];
  for (var j = 0; j < n; j++) {
    p = x * p + A[n - j - 1];
  }
  return p;
}
//计算: y(2) = 3x^3 + 2x^2 + x -1;
var A = [-1, 1, 2, 3];
var y = horner(A, 2);
alert(y);//33

多数问题：

一个元素个数为n的数组，希望快速找出其中大于出现次数>n/2的元素（该元素也称为多数元素）。通常可用于选票系统，快速判定某个候选人的票数是否过半。最优算法如下：

//找出数组A中“可能存在”的多数元素
function candidate(A, m) {
  var count = 1, c = A[m], n = A.length - 1;
  while (m < n && count > 0) {
    m++;
    if (A[m] == c) {
      count++;
    }
    else {
      count--;
    }
  }
  if (m == n) {
    return c;
  }
  else {
    return candidate(A, m + 1);
  }
}
//寻找多数元素
//时间复杂度O(n)
function majority(A) {
  var c = candidate(A, 0);
  var count = 0;
  //找出的c，可能是多数元素，也可能不是，
  //必须再数一遍，以确保结果正确
  for (var i = 0; i < A.length; i++) {
    if (A[i] == c) {
      count++;
    }
  }
  //如果过半，则确定为多数元素
  if (count > Math.floor(A.length / 2)) {
    return c;
  }
  return null;
}
var m = majority([3, 2, 3, 3, 4, 3]);
alert(m);

以上算法基于这样一个结论：在原序列中去除两个不同的元素后，那么在原序列中的多数元素在新序列中还是多数元素

证明如下：

如果原序列的元素个数为n，多数元素出现的次数为x，则 x/n > 1/2
去掉二个不同的元素后，
a)如果去掉的元素中不包括多数元素，则新序列中 ，原先的多数元素个数/新序列元素总数 = x/(n-2) ，因为x/n > 1/2 ，所以 x/(n-2) 也必然>1/2
b)如果去掉的元素中包含多数元素，则新序列中 ，原先的多数元素个数/新序列元素总数 = (x-1)/(n-2) ，因为x/n > 1/2 =》 x>n/2 代入 (x-1)/(n-2) 中，
有 (x-1)/(n-2) > (n/2 -1)/(n-2) = 2(n-2)/(n-2) = 1/2

下一个问题：全排列

function swap(A, i, j) {
  var t = A[i];
  A[i] = A[j];
  A[j] = t;
}
function println(msg) {
  document.write(msg + "<br/>");
}
//全排列算法
function perm(P, m) {
  var n = P.length - 1;
  if (m == n) {
    //完成一个新排列时，输出
    println(P);
    return;
  }
  for (var j = m; j <= n; j++) {
    //将起始元素与后面的每个元素交换
    swap(P, j, m);
    //在前m个元素已经排好的基础上
    //再加一个元素进行新排列
    perm(P, m + 1);
    //把j与m换回来，恢复递归调用前的“现场"，
    //否则因为递归调用前，swap已经将原顺序破坏了，
    //导致后面生成排序时，可能生成重复
    swap(P, j, m);
  }
}
perm([1, 2, 3], 0);
//1,2,3
//1,3,2
//2,1,3
//2,3,1
//3,2,1
//3,1,2

分治法：

要点：将问题划分成二个子问题时，尽量让子问题的规模大致相等。这样才能最大程度的体现一分为二，将问题规模以对数折半缩小的优势。

//打印输出(调试用)
function println(msg) {
  document.write(msg + "<br/>");
}
//数组中i,j位置的元素交换(辅助函数)
function swap(A, i, j) {
  var t = A[i];
  A[i] = A[j];
  A[j] = t;
}
//寻找数组A中的最大、最小值(分治法实现)
function findMinMaxDiv(A, low, high) {
  //最小规模子问题的解
  if (high - low == 1) {
    if (A[low] < A[high]) {
      return [A[low], A[high]];
    }
    else {
      return [A[high], A[low]];
    }
  }
  var mid = Math.floor((low + high) / 2);
  //在前一半元素中寻找子问题的解
  var r1 = findMinMaxDiv(A, low, mid);
  //在后一半元素中寻找子问题的解
  var r2 = findMinMaxDiv(A, mid + 1, high);
  //把二部分的解合并
  var x = r1[0] > r2[0] &#63; r2[0] : r1[0];
  var y = r1[1] > r2[1] &#63; r1[1] : r2[1];
  return [x, y];
}
var r = findMinMaxDiv([1, 2, 3, 4, 5, 6, 7, 8], 0, 7);
println(r); //1,8
//二分搜索(分治法实现)
//输入：A为已按非降序排列的数组
//x 为要搜索的值
//low,high搜索的起、止索引范围
//返回：如果找到，返回下标，否则返回-1
function binarySearchDiv(A, x, low, high) {
  if (low > high) {
    return -1;
  }
  var mid = Math.floor((low + high) / 2);
  if (x == A[mid]) {
    return mid;
  }
  else if (x < A[mid]) {
    return binarySearchDiv(A, x, low, mid - 1);
  }
  else {
    return binarySearchDiv(A, x, mid + 1, high);
  }
}
var f = binarySearchDiv([1, 2, 3, 4, 5, 6, 7], 4, 0, 6);
println(f); //3
//将数组A，以low位置的元素为界，划分为前后二半
//n为待处理的索引范围上限
function split(A, low, n) {
  if (n >= A.length - 1) {
    n = A.length - 1;
  }
  var i = low;
  var x = A[low];
  //二个指针一前一后“跟随”，
  //最前面的指针发现有元素比分界元素小时，换到前半部
  //后面的指针再紧跟上，“夫唱妇随”一路到头
  for (var j = low + 1; j <= n; j++) {
    if (A[j] <= x) {
      i++;
      if (i != j) {
        swap(A, i, j);
      }
    }
  }
  //经过上面的折腾后，除low元素外，其它的元素均以就位
  //最后需要把low与最后一个比low位置小的元素交换，
  //以便把low放在分水岭位置上
  swap(A, low, i);
  return [A, i];
}
var A = [5, 1, 2, 6, 3];
var b = split(A, 0, A.length - 1);
println(b[0]); //3,1,2,5,6
//快速排序 
function quickSort(A, low, high) {
  var w = high;
  if (low < high) {
    var t = split(A, low, w); //分治思路，先分成二半
    w = t[1];
    //在前一半求解
    quickSort(A, low, w - 1);
    //在后一半求解
    quickSort(A, w + 1, high);
  }
}
var A = [5, 6, 4, 7, 3];
quickSort(A, 0, A.length - 1);
println(A); //3,4,5,6,7

split算法的思想应用：

设A[1..n]是一个整数集，给出一算法重排数组A中元素，使得所有的负整数放到所有非负整数的左边，你的算法的运行时间应当为Θ(n)

function sort1(A) {
  var i = 0, j = A.length - 1;
  while (i < j) {
    if (A[i] >= 0 && A[j] >= 0) {
      j--;
    }
    else if (A[i] < 0 && A[j] < 0) {
      i++;
    }
    else if (A[i] > 0 && A[j] < 0) {
      swap(A, i, j);
      i++;
      j--;
    }
    else {
      i++;
      j--;
    }
  }
}
function sort2(A) {
  if (A.length <= 1) { return; }
  var i = 0;
  for (var j = i + 1; j < A.length; j++) {
    if (A[j] < 0 && A[i] >= 0) {
      swap(A, i, j);
      i++;
    }
  }
}
var a = [1, -2, 3, -4, 5, -6, 0];
sort1(a);
println(a);//-6,-2,-4,3,5,1,0
var b = [1, -2, 3, -4, 5, -6, 0];
sort2(b);
println(b);//-2,-4,-6,1,5,3,0

希望本文所述对大家JavaScript程序设计有所帮助。