이진 트리의 설정 및 순회에 대해 이 기사에서는 자세히 소개하고 선순 이진 트리 순회, 순차 이진 트리 순회, 후순 이진 트리 순회 알고리즘도 설명하며 코드는 다음과 같습니다. 모두가 더 명확하게 볼 수 있도록 인용했습니다. 이 글의 서론은 이해하기 쉽도록 이진 트리와 이진 검색 트리로 시작해야 합니다. apache php mysql
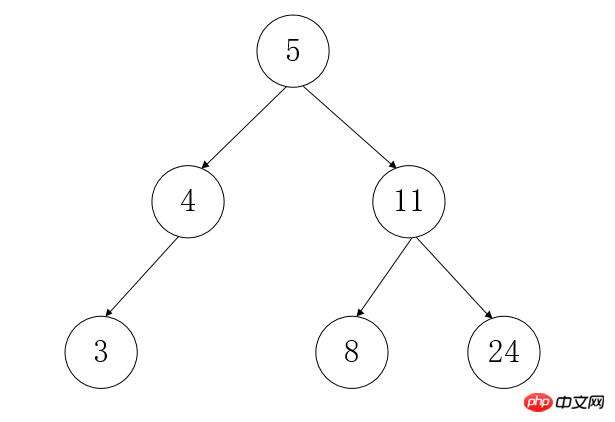
노드: 트리의 각 요소를 노드라고 합니다.
루트 노드: 전체 트리의 정점에 위치한 노드입니다. 트리, 위의 그림 5와 같이 부모 노드가 없습니다
자식 노드: 다른 노드의 자손
리프 노드: 그림 3과 같이 자식 노드가 없는 요소를 리프 노드라고 합니다. 8 24
이진 트리: 이진 트리 트리는 데이터 구조이며 조직 관계는 자연의 나무와 같습니다. 공식 언어의 정의는 다음과 같습니다. 이는 비어 있거나 루트라는 요소와 각각 왼쪽 하위 트리와 오른쪽 하위 트리라고 하는 두 개의 분리된 이진 트리로 구성된 유한 요소 집합입니다.
이진 검색 트리:
이진 검색 트리는 BST(이진 검색 트리)라고도 하며 왼쪽 노드에는 부모 노드보다 작은 값을, 오른쪽 노드에는 부모 노드보다 큰 값만 저장할 수 있습니다. 위의 그림은 이진 검색 트리를 보여줍니다.
먼저 이진 검색 트리를 나타내는 클래스를 만듭니다. 노드를 만들려면 내부에 Node 클래스가 있어야 합니다.
function BinarySearchTree () {
var Node = function(key) {
this.key = key,
this.left = null,
this.right = null
}
var root = null
}또한 몇 가지 메서드가 있어야 합니다.
insert(key) 새 키 삽입
inOrderTraverse()는 트리의 순회를 수행하고 결과를 인쇄합니다.
preOrderTraverse()는 트리의 선순 순회를 수행하고 결과를 인쇄합니다.
postOrderTraverse()는 후순 순회를 수행합니다. , 그리고 결과를 인쇄합니다
search(key)는 트리에서 키를 검색하고, 존재하면 true를 반환하고, 존재하지 않으면 false를 반환합니다.
findMin()은 트리에서 최소값을 반환합니다. tree
findMax()는 트리를 반환합니다.
remove(key)의 최대값은 트리에서 키를 삭제합니다.
트리에 새 키를 삽입합니다. 홈페이지에서는 새 노드 클래스 인스턴스를 나타내기 위해 노드를 생성해야 하므로 노드 클래스를 새로 만들고 삽입해야 하는 키 값을 전달해야 합니다. 그런 다음 왼쪽 및 오른쪽 노드가 null인 새 노드로 자동으로 초기화됩니다. 먼저, 트리가 비어 있는지 판단하고, 비어 있으면 새로 삽입된 노드가 루트 노드로 사용됩니다. 비어 있지 않으면 insertNode() 메서드를 호출하고, 루트 노드와 새 노드를
this.insert = function(key) {
var newNode = new Node(key)
if(root === null) {
root = newNode
} else {
insertNode(root, newNode)
}
}insertNode() 메서드를 정의하면 이 메서드는 새로 추가된 노드의 적절한 위치를 찾기 위해 자신을 재귀적으로 호출합니다
var insertNode = function(node, newNode) {
if (newNode.key <= node.key) {
if (node.left === null) {
node.left = newNode
}else {
insertNode(node.left, newNode)
}
}else {
if (node.right === null) {
node.right = newNode
}else {
insertNode(node.right, newNode)
}
}
}순서대로 탐색 메서드를 완성합니다
this.inOrderTraverse = function() {
inOrderTraverseNode(root)
}이 메서드는 각 노드의 키 값을 인쇄하려면 재귀적 종료 조건이 필요합니다. 들어오는 노드가 null인지 확인하세요. . 그렇지 않은 경우 계속해서 자신을 호출하여 노드의 왼쪽 및 오른쪽 노드를 확인합니다. :
var inOrderTraverseNode = function(node) {
if (node !== null) {
inOrderTraverseNode(node.left)
console.log(node.key)
inOrderTraverseNode(node.right)
}
}선순서 순회, 후순순회
이런 식으로 전체 트리를 순회할 수 있습니다. 트리는 순서대로 순회됩니다.
// 实现先序遍历
this.preOrderTraverse = function() {
preOrderTraverseNode(root)
}
var preOrderTraverseNode = function(node) {
if (node !== null) {
console.log(node.key)
preOrderTraverseNode(node.left)
preOrderTraverseNode(node.right)
}
}
// 实现后序遍历
this.postOrderTraverse = function() {
postOrderTraverseNode(root)
}
var postOrderTraverseNode = function(node) {
if (node !== null) {
postOrderTraverseNode(node.left)
postOrderTraverseNode(node.right)
console.log(node.key)
}
} function BinarySearchTree () {
var Node = function(key) {
this.key = key,
this.left = null,
this.right = null
}
var root = null
//插入节点
this.insert = function(key) {
var newNode = new Node(key)
if(root === null) {
root = newNode
} else {
insertNode(root, newNode)
}
}
var insertNode = function(node, newNode) {
if (newNode.key <= node.key) {
if (node.left === null) {
node.left = newNode
}else {
insertNode(node.left, newNode)
}
}else {
if (node.right === null) {
node.right = newNode
}else {
insertNode(node.right, newNode)
}
}
}
//实现中序遍历
this.inOrderTraverse = function() {
inOrderTraverseNode(root)
}
var inOrderTraverseNode = function(node) {
if (node !== null) {
inOrderTraverseNode(node.left)
console.log(node.key)
inOrderTraverseNode(node.right)
}
}
// 实现先序遍历
this.preOrderTraverse = function() {
preOrderTraverseNode(root)
}
var preOrderTraverseNode = function(node) {
if (node !== null) {
console.log(node.key)
preOrderTraverseNode(node.left)
preOrderTraverseNode(node.right)
}
}
// 实现后序遍历
this.postOrderTraverse = function() {
postOrderTraverseNode(root)
}
var postOrderTraverseNode = function(node) {
if (node !== null) {
postOrderTraverseNode(node.left)
postOrderTraverseNode(node.right)
console.log(node.key)
}
}
}var arr = [9,6,3,8,12,15]
var tree = new BinarySearchTree()
arr.map(item => {
tree.insert(item)
})
tree.inOrderTraverse()
tree.preOrderTraverse()
tree.postOrderTraverse() 출력 결과 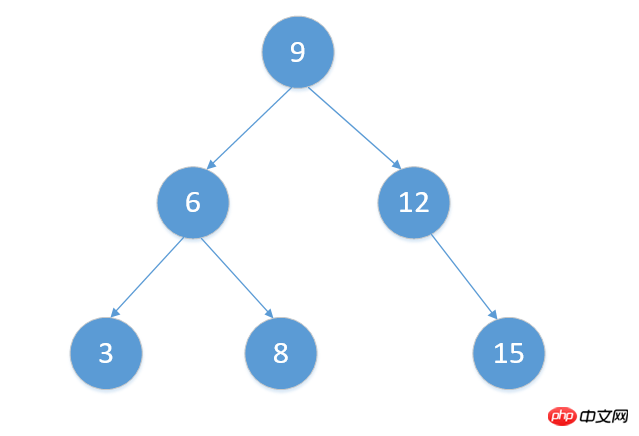
<p>3</p>6<p>8<code><br/>3<br/>6<br/>8<br/>9<br/>12<br/>15<br/>先序遍历:<br/>9<br/>6<br/>3<br/>8<br/>12<br/>15<br/>
后序遍历:<br/>3<br/>8<br/>6<br/>15<br/>12<br/>9<br/>9
15
선주문 순회:<p>9</p> 6<p> 3</p>8🎜12🎜15🎜🎜🎜Postorder traversal: 🎜3🎜8🎜6🎜15🎜12🎜9🎜🎜🎜분명히 결과는 예상대로이므로 다음을 사용합니다. 위의 JavaScript 코드는 트리에 노드 삽입과 세 가지 탐색 방법을 구현하는 동시에 이진 검색 트리에서 가장 왼쪽 노드의 값이 가장 작다는 것이 분명합니다. , 이진 검색 트리는 쉽게 최대값과 최소값을 얻을 수 있습니다 🎜🎜최소값과 최대값을 찾는 방법 🎜🎜? 실제로 루트 노드를 minNode/또는 maxNode 메소드에 전달한 다음 루프를 통해 왼쪽(minNode)/오른쪽(maxNode)에 있는 노드가 null🎜🎜인 것을 루프를 통해 판단하면 됩니다🎜🎜구현 코드: 🎜 // 查找最小值
this.findMin = function() {
return minNode(root)
}
var minNode = function(node) {
if (node) {
while (node && node.left !== null) {
node = node.left
}
return node.key
}
return null
}
// 查找最大值
this.findMax = function() {
return maxNode(root)
}
var maxNode = function (node) {
if(node) {
while (node && node.right !== null) {
node =node.right
}
return node.key
}
return null
}this.search = function(key) {
return searchNode(root, key)
}同样,实现它需要定义一个辅助方法,这个方法首先会检验node的合法性,如果为null,直接退出,并返回fasle。如果传入的key比当前传入node的key值小,它会继续递归查找node的左侧节点,反之,查找右侧节点。如果找到相等节点,直接退出,并返回true
var searchNode = function(node, key) {
if (node === null) {
return false
}
if (key < node.key) {
return searchNode(node.left, key)
}else if (key > node.key) {
return searchNode(node.right, key)
}else {
return true
}
}移除节点的实现情况比较复杂,它会有三种不同的情况:
需要移除的节点是一个叶子节点
需要移除的节点包含一个子节点
需要移除的节点包含两个子节点
和实现搜索指定节点一元,要移除某个节点,必须先找到它所在的位置,因此移除方法的实现中部分代码和上面相同:
// 移除节点
this.remove = function(key) {
removeNode(root,key)
}
var removeNode = function(node, key) {
if (node === null) {
return null
}
if (key < node.key) {
node.left = removeNode(node.left, key)
return node
}else if(key > node.key) {
node.right = removeNode(node.right,key)
return node
}else{
//需要移除的节点是一个叶子节点
if (node.left === null && node.right === null) {
node = null
return node
}
//需要移除的节点包含一个子节点
if (node.letf === null) {
node = node.right
return node
}else if (node.right === null) {
node = node.left
return node
}
//需要移除的节点包含两个子节点
var aux = findMinNode(node.right)
node.key = aux.key
node.right = removeNode(node.right, axu.key)
return node
}
}
var findMinNode = function(node) {
if (node) {
while (node && node.left !== null) {
node = node.left
}
return node
}
return null
}其中,移除包含两个子节点的节点是最复杂的情况,它包含左侧节点和右侧节点,对它进行移除主要需要三个步骤:
需要找到它右侧子树中的最小节点来代替它的位置
将它右侧子树中的最小节点移除
将更新后的节点的引用指向原节点的父节点
有点绕儿,但必须这样,因为删除元素后的二叉搜索树必须保持它的排序性质
tree.remove(8) tree.inOrderTraverse()
打印结果:
3<br/>6<br/>9<br/>12<br/>15<br/>
8 这个节点被成功删除了,但是对二叉查找树进行中序遍历依然是保持排序性质的
到这里,一个简单的二叉查找树就基本上完成了,我们为它实现了,添加、查找、删除以及先中后三种遍历方法
但是实际上这样的二叉查找树是存在一些问题的,当我们不断的添加更大/更小的元素的时候,会出现如下情况:
tree.insert(16) tree.insert(17) tree.insert(18)
来看看现在整颗树的情况:
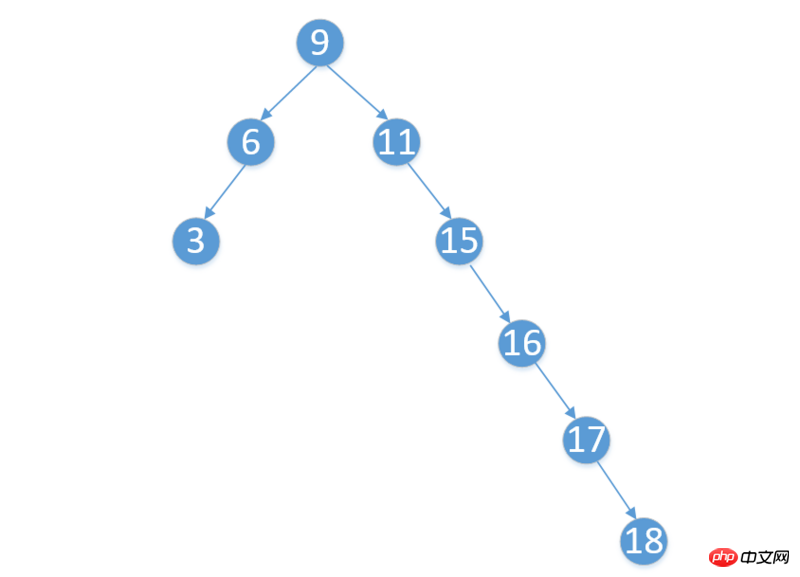
看图片容易得出它是不平衡的,这又会引出平衡树的概念,要解决这个问题,还需要更复杂的实现,例如:AVL树,红黑树 哎,之后再慢慢去学习吧
相关文章:
위 내용은 js_앞, 중간, 뒤 순서로 이진 트리 탐색을 위한 세 가지 알고리즘_간단한 이진 트리 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!