JavaScript를 사용하여 두 장소 사이의 거리를 어떻게 계산하나요? 다음 기사에서는 경도와 위도를 통해 두 장소 사이의 거리를 계산하는 JavaScript를 소개할 것입니다.
최근 업무상 경도와 위도를 기준으로 두 장소 사이의 거리를 계산하는 방법을 인터넷에서 검색해 보니 기하학적인 방법이나 그림을 그리는 방법, 보조선을 잔뜩 만드는 방법, 그런 다음 추론을 증명하거나 아무 말도하지 않고 직접 공식을 공식화합니다. 이 기사에서는 이 거리를 구하는 이해하기 쉬운 방법을 소개합니다.
지구는 불규칙한 타원체로 계산을 단순화하기 위해 구로 간주합니다.
구면의 두 지점 사이의 최단 거리는 두 지점을 통과하는 대원의 작은 호의 길이입니다.
아이디어는 다음과 같습니다.
호 길이 ← 현 길이(두 점 사이의 거리) ← 두 점 좌표(직사각형 좌표) ← 위도 및 경도
을 가정합니다. 지구의 반지름은 $R$
지구의 중심을 E 0° N 0°에 연결한 선이 x축입니다
지구의 중심을 E 90° N 0°에 연결한 선이 y입니다 -axis
지구 중심과 E 0° N 90°를 연결한 선이 Z축입니다
지구 표면에 $A$ 점이 있고 경도는 $e$, 위도는 $n$, 단위는 라디안입니다
그러면 $A$의 좌표는 다음과 같이 표현할 수 있습니다.$$ x = R cdot cos(n) cdot cos(e)\ y = R cdot cos(n) cdot sin(e)\ z = R cdot sin(n) $$
Codeconst R = 6371
const {cos, sin, PI} = Math
let getPoint = (e, n) => {
//首先将角度转为弧度
e *= PI/180
n *= PI/180
reutrn {
x: R*cos(n)*cos(e),
y: R*cos(n)*sin(e),
z: R*sin(n)
}
}3 현 길이를 기준으로 호 길이를 구하세요
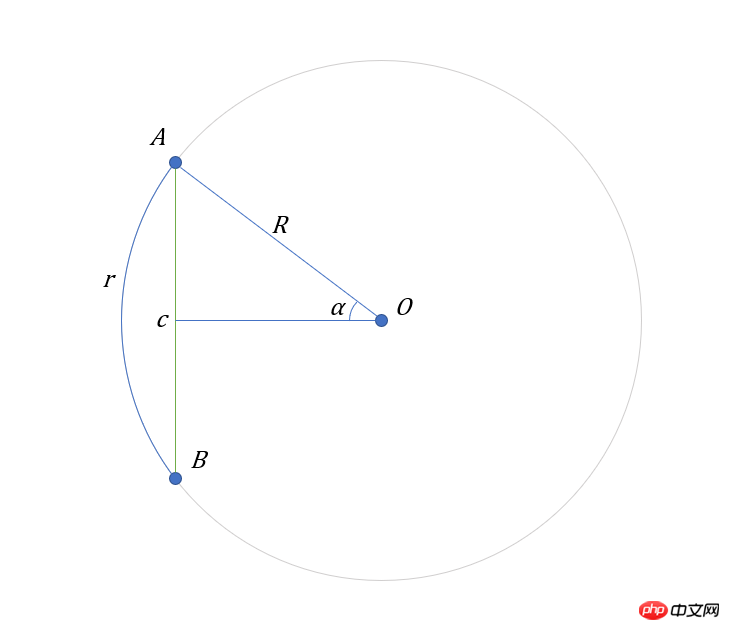 이제 우리는 현의 길이 $c$, 반경 $R$을 알고 호의 길이 $r$를 요구합니다.
이제 우리는 현의 길이 $c$, 반경 $R$을 알고 호의 길이 $r$를 요구합니다.
$$
알파 = 아크사인(c/2/R)\
r = 2알파 cdot R
USD
위 내용은 Javascript는 위도와 경도를 기준으로 두 장소 사이의 거리를 계산합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!



