Python의 순차 목록 알고리즘의 복잡성에 대한 지식 소개
이 기사는 Python의 시퀀스 테이블 알고리즘의 복잡성에 대한 관련 지식을 제공합니다. 이는 특정 참조 가치가 있으므로 도움이 될 수 있습니다.
1. 알고리즘 복잡도 소개
알고리즘의 시간적, 공간적 특성에서 가장 중요한 것은 크기와 추세이므로 복잡도를 측정하는 함수 상수 인자는 무시할 수 있습니다.
Big O 표기법 일반적으로 특정 알고리즘의 점근적 시간 복잡도를 사용합니다. 일반적으로 사용되는 점근적 복잡도 함수의 복잡도를 비교하면 다음과 같습니다.
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
시간 복잡도를 도입한 예입니다. 두 코드 예를 비교하여 계산 결과를 확인하세요.
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a+b+c ==1000 and a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")

rreee
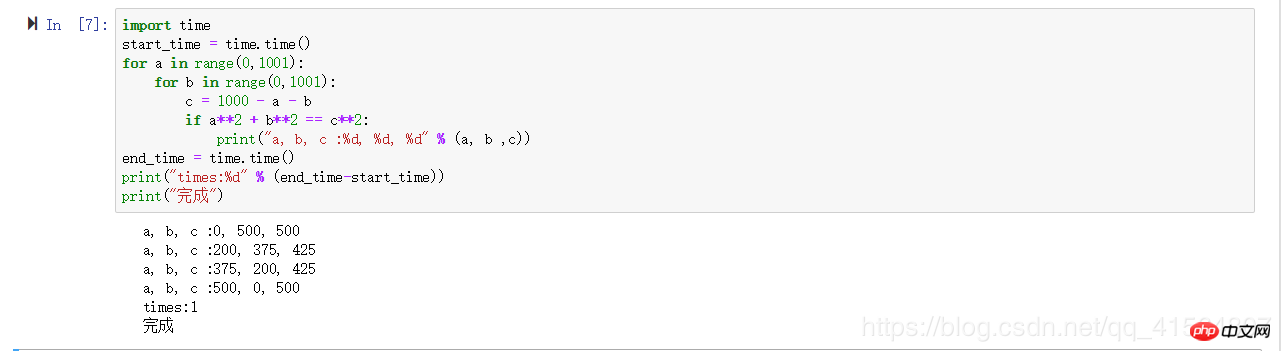
시간 복잡도 계산 방법:
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")2. 순차 목록의 시간 복잡도
목록의 시간 복잡도 테스트
# 时间复杂度计算 # 1.基本步骤,基本操作,复杂度是O(1) # 2.顺序结构,按加法计算 # 3.循环,按照乘法 # 4.分支结构采用其中最大值 # 5.计算复杂度,只看最高次项,例如n^2+2的复杂度是O(n^2)
출력 결과

목록에 있는 메서드의 복잡성:
rreee
사전에 있는 메서드의 복잡성(보충)
# 测试
from timeit import Timer
def test1():
list1 = []
for i in range(10000):
list1.append(i)
def test2():
list2 = []
for i in range(10000):
# list2 += [i] # +=本身有优化,所以不完全等于list = list + [i]
list2 = list2 + [i]
def test3():
list3 = [i for i in range(10000)]
def test4():
list4 = list(range(10000))
def test5():
list5 = []
for i in range(10000):
list5.extend([i])
timer1 = Timer("test1()","from __main__ import test1")
print("append:",timer1.timeit(1000))
timer2 = Timer("test2()","from __main__ import test2")
print("+:",timer2.timeit(1000))
timer3 = Timer("test3()","from __main__ import test3")
print("[i for i in range]:",timer3.timeit(1000))
timer4 = Timer("test4()","from __main__ import test4")
print("list(range):",timer4.timeit(1000))
timer5 = Timer("test5()","from __main__ import test5")
print("extend:",timer5.timeit(1000))
3. 시퀀스 테이블의 데이터 구조
시퀀스 테이블의 전체 정보는 두 부분으로 구성됩니다. 한 부분은 테이블의 요소 집합이고 다른 부분은 올바른 결과를 얻기 위해 기록해야 하는 정보입니다. 이 부분의 정보에는 주로 요소 저장이 포함됩니다. 영역의 용량과 현재 테이블의 요소 수라는 두 가지 항목이 있습니다.
헤더와 데이터 영역의 결합: 통합 구조: 헤더 정보(기록 용량 및 기존 요소 수)와 지속적인 저장을 위한 데이터 영역
분리 구조: 헤더 정보 데이터 영역과 데이터 영역은 연속적으로 저장되지는 않습니다. 실제 데이터 영역을 가리키도록 주소 단위를 저장하는 데 사용되는 정보가 있습니다.
둘 사이의 차이점과 장단점:
# 列表方法中复杂度 # index O(1) # append 0(1) # pop O(1) 无参数表示是从尾部向外取数 # pop(i) O(n) 从指定位置取,也就是考虑其最复杂的状况是从头开始取,n为列表的长度 # del O(n) 是一个个删除 # iteration O(n) # contain O(n) 其实就是in,也就是说需要遍历一遍 # get slice[x:y] O(K) 取切片,即K为Y-X # del slice O(n) 删除切片 # set slice O(n) 设置切片 # reverse O(n) 逆置 # concatenate O(k) 将两个列表加到一起,K为第二个列表的长度 # sort O(nlogn) 排序,和排序算法有关 # multiply O(nk) K为列表的长度
# 字典中的复杂度 # copy O(n) # get item O(1) # set item O(1) 设置 # delete item O(1) # contains(in) O(1) 字典不用遍历,所以可以一次找到 # iteration O(n)
4. Python의 가변 공간 확장 전략
1. 빈 테이블(또는 작은 테이블)을 생성할 때 시스템은 8개의 요소를 수용할 수 있는 저장 영역을 할당합니다.
2. 삽입 작업(삽입, 추가)을 수행할 때 해당 영역이 저장될 때 3. 이때 테이블이 이미 매우 큰 경우(임계값은 50,000) 정책을 변경하고 두 배로 늘리는 방법을 채택합니다. 너무 많은 여유 공간을 피하기 위해.
위 내용은 Python의 순차 목록 알고리즘의 복잡성에 대한 지식 소개의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7569
7569
 15
15
 1386
1386
 52
52
 87
87
 11
11
 62
62
 19
19
 28
28
 108
108
 Python vs. JavaScript : 커뮤니티, 라이브러리 및 리소스
Apr 15, 2025 am 12:16 AM
Python vs. JavaScript : 커뮤니티, 라이브러리 및 리소스
Apr 15, 2025 am 12:16 AM
Python과 JavaScript는 커뮤니티, 라이브러리 및 리소스 측면에서 고유 한 장점과 단점이 있습니다. 1) Python 커뮤니티는 친절하고 초보자에게 적합하지만 프론트 엔드 개발 리소스는 JavaScript만큼 풍부하지 않습니다. 2) Python은 데이터 과학 및 기계 학습 라이브러리에서 강력하며 JavaScript는 프론트 엔드 개발 라이브러리 및 프레임 워크에서 더 좋습니다. 3) 둘 다 풍부한 학습 리소스를 가지고 있지만 Python은 공식 문서로 시작하는 데 적합하지만 JavaScript는 MDNWebDocs에서 더 좋습니다. 선택은 프로젝트 요구와 개인적인 이익을 기반으로해야합니다.
 터미널 VSCODE에서 프로그램을 실행하는 방법
Apr 15, 2025 pm 06:42 PM
터미널 VSCODE에서 프로그램을 실행하는 방법
Apr 15, 2025 pm 06:42 PM
vs 코드에서는 다음 단계를 통해 터미널에서 프로그램을 실행할 수 있습니다. 코드를 준비하고 통합 터미널을 열어 코드 디렉토리가 터미널 작업 디렉토리와 일치하는지 확인하십시오. 프로그래밍 언어 (예 : Python의 Python Your_file_name.py)에 따라 실행 명령을 선택하여 성공적으로 실행되는지 여부를 확인하고 오류를 해결하십시오. 디버거를 사용하여 디버깅 효율을 향상시킵니다.
 Python에서 비주얼 스튜디오 코드를 사용할 수 있습니다
Apr 15, 2025 pm 08:18 PM
Python에서 비주얼 스튜디오 코드를 사용할 수 있습니다
Apr 15, 2025 pm 08:18 PM
VS 코드는 파이썬을 작성하는 데 사용될 수 있으며 파이썬 애플리케이션을 개발하기에 이상적인 도구가되는 많은 기능을 제공합니다. 사용자는 다음을 수행 할 수 있습니다. Python 확장 기능을 설치하여 코드 완료, 구문 강조 및 디버깅과 같은 기능을 얻습니다. 디버거를 사용하여 코드를 단계별로 추적하고 오류를 찾아 수정하십시오. 버전 제어를 위해 git을 통합합니다. 코드 서식 도구를 사용하여 코드 일관성을 유지하십시오. 라인 도구를 사용하여 잠재적 인 문제를 미리 발견하십시오.
 VScode 확장자가 악의적입니까?
Apr 15, 2025 pm 07:57 PM
VScode 확장자가 악의적입니까?
Apr 15, 2025 pm 07:57 PM
VS 코드 확장은 악의적 인 코드 숨기기, 취약성 악용 및 합법적 인 확장으로 자위하는 등 악성 위험을 초래합니다. 악의적 인 확장을 식별하는 방법에는 게시자 확인, 주석 읽기, 코드 확인 및주의해서 설치가 포함됩니다. 보안 조치에는 보안 인식, 좋은 습관, 정기적 인 업데이트 및 바이러스 백신 소프트웨어도 포함됩니다.
 Windows 8에서 코드를 실행할 수 있습니다
Apr 15, 2025 pm 07:24 PM
Windows 8에서 코드를 실행할 수 있습니다
Apr 15, 2025 pm 07:24 PM
VS 코드는 Windows 8에서 실행될 수 있지만 경험은 크지 않을 수 있습니다. 먼저 시스템이 최신 패치로 업데이트되었는지 확인한 다음 시스템 아키텍처와 일치하는 VS 코드 설치 패키지를 다운로드하여 프롬프트대로 설치하십시오. 설치 후 일부 확장은 Windows 8과 호환되지 않을 수 있으며 대체 확장을 찾거나 가상 시스템에서 새로운 Windows 시스템을 사용해야합니다. 필요한 연장을 설치하여 제대로 작동하는지 확인하십시오. Windows 8에서는 VS 코드가 가능하지만 더 나은 개발 경험과 보안을 위해 새로운 Windows 시스템으로 업그레이드하는 것이 좋습니다.
 파이썬 : 자동화, 스크립팅 및 작업 관리
Apr 16, 2025 am 12:14 AM
파이썬 : 자동화, 스크립팅 및 작업 관리
Apr 16, 2025 am 12:14 AM
파이썬은 자동화, 스크립팅 및 작업 관리가 탁월합니다. 1) 자동화 : 파일 백업은 OS 및 Shutil과 같은 표준 라이브러리를 통해 실현됩니다. 2) 스크립트 쓰기 : PSUTIL 라이브러리를 사용하여 시스템 리소스를 모니터링합니다. 3) 작업 관리 : 일정 라이브러리를 사용하여 작업을 예약하십시오. Python의 사용 편의성과 풍부한 라이브러리 지원으로 인해 이러한 영역에서 선호하는 도구가됩니다.
 VScode 란 무엇입니까?
Apr 15, 2025 pm 06:45 PM
VScode 란 무엇입니까?
Apr 15, 2025 pm 06:45 PM
VS Code는 Full Name Visual Studio Code로, Microsoft가 개발 한 무료 및 오픈 소스 크로스 플랫폼 코드 편집기 및 개발 환경입니다. 광범위한 프로그래밍 언어를 지원하고 구문 강조 표시, 코드 자동 완료, 코드 스 니펫 및 스마트 프롬프트를 제공하여 개발 효율성을 향상시킵니다. 풍부한 확장 생태계를 통해 사용자는 디버거, 코드 서식 도구 및 GIT 통합과 같은 특정 요구 및 언어에 확장을 추가 할 수 있습니다. VS 코드에는 코드에서 버그를 신속하게 찾아서 해결하는 데 도움이되는 직관적 인 디버거도 포함되어 있습니다.
 코드를 실행할 수 있습니다
Apr 15, 2025 pm 08:21 PM
코드를 실행할 수 있습니다
Apr 15, 2025 pm 08:21 PM
예, 대 코드는 Python 코드를 실행할 수 있습니다. 대 코드에서 Python을 효율적으로 실행하려면 다음 단계를 완료하십시오. Python 통역사를 설치하고 환경 변수를 구성하십시오. 대 코드에 파이썬 확장을 설치하십시오. 명령 줄을 통해 대 코드 터미널에서 파이썬 코드를 실행하십시오. VS Code의 디버깅 기능 및 코드 서식을 사용하여 개발 효율성을 향상시킵니다. 좋은 프로그래밍 습관을 채택하고 성능 분석 도구를 사용하여 코드 성능을 최적화하십시오.




