이 글은 JavaScript의 바이너리 트리(바이너리 힙)에 대한 소개(코드 예제)를 제공합니다. 이는 특정 참조 가치가 있으므로 도움이 필요한 친구들이 참고할 수 있기를 바랍니다.
이진 트리
이진 트리(Binary Tree)는 트리 구조의 특징은 각 노드가 최대 2개의 가지 노드만 갖는다는 것입니다. 이진 트리는 일반적으로 루트 노드, 가지 노드, 리프 노드로 구성됩니다. 각 분기 노드를 종종 하위 트리라고 합니다.
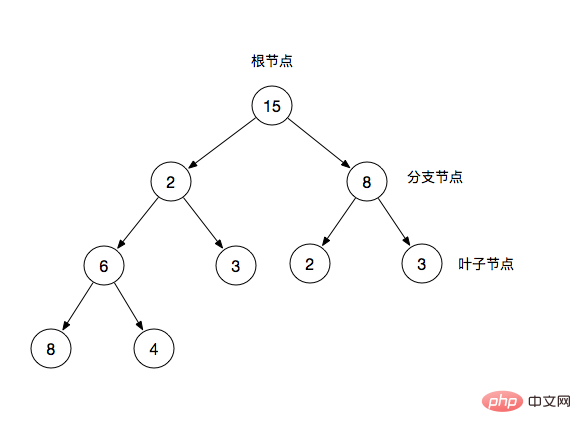
루트 노드: 이진 트리의 최상위 노드
분기 노드: 루트 노드를 제외하고 리프 노드가 있음
리프 노드: 자신만 제외하고 다른 자식 노드 없음
자주 사용되는 용어
이진 트리에서는 이를 설명하기 위해 부모 노드와 자식 노드를 사용하는 경우가 많습니다. 예를 들어 그림의 2는 6과 3의 부모 노드이고, 반대로 6과 3은 자식 노드입니다. 2
3개의 이진 트리 속성
이진 트리의 i번째 수준에는 최대 2^i-1개의 노드
i=1이 있습니다. =1, 단 하나의 루트 노드가 있습니다. 2^(i-1) = 2^0 = 1
깊이 k인 이진 트리에는 최대 2^k-1개의 노드가 있습니다
i= 2, 2^k-1 = 2^2 - 1 = 3개 노드
임의의 이진 트리 T에 대해 요약 포인트 개수가 n0이고 차수가 2인 노드 개수(하위 트리 개수는 2)인 경우 n2이면 n0=n2+1
트리의 노드 수는 최소 1개이지만 이진 트리의 노드 수는 0이 될 수 있습니다
트리의 노드 최대 차수(노드 수)는 제한이 없지만 이진 트리의 노드 최대 차수는 2
트리 이진 트리의 노드는 왼쪽으로 나누어지지 않습니다. 그리고 오른쪽, 이진 트리의 노드는 왼쪽과 오른쪽으로 나뉘어져 있는데
이진 트리는 완전 이진 트리(완전 이진 트리)와 완전 이진 트리(완전 이진 트리)
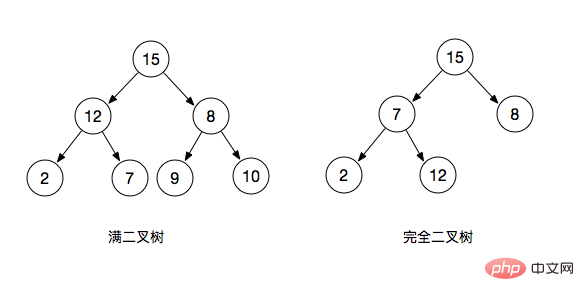
완전 이진 트리: 1 깊이 k이고 2^k - 1개의 노드를 갖는 이진 트리를 완전 이진 트리라고 합니다
완전 이진 트리: 완전 이진 트리는 마지막 레이어의 왼쪽이 가득 차 있음을 의미합니다. 오른쪽이 가득 차 있을 수도 있고 아닐 수도 있고 나머지 레이어도 가득 차게 됩니다. 이진 트리를 완전 이진 트리라고 합니다(완전 이진 트리도 완전 이진 트리입니다)
배열을 사용하여 이진 트리의 구조를 루트 노드부터 시작하여 위에서 위로 배열합니다. 그런 다음 아래 그림과 같이 왼쪽에서 오른쪽으로 완전한 이진 트리를 채웁니다.
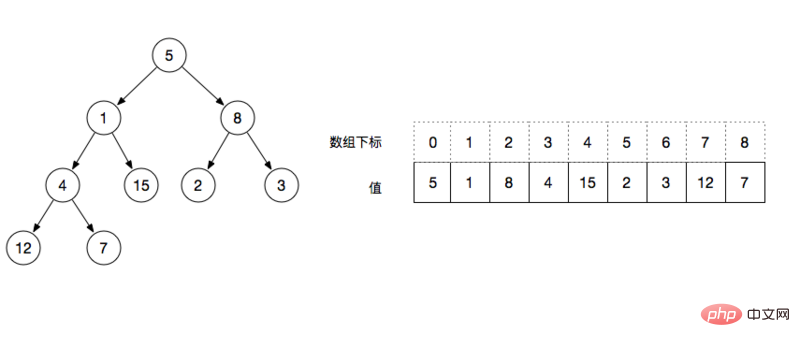위 그림을 통해 배열로 표현된 완전한 이진 트리가 다음 속성을 갖는다는 것을 분석할 수 있습니다.
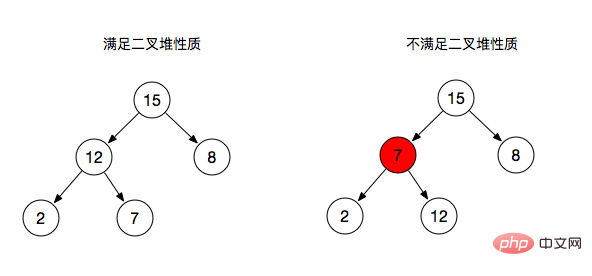
이라고 합니다. 위 그림에서 볼 수 있듯이:
배열 길이 저장
class Heap{
constructor(arr){
this.data = [...arr];
this.size = this.data.length;
}
}max-heapify는 최대 힙 속성을 충족하지 못하는 각 분기 노드를 조정하는 연산입니다.
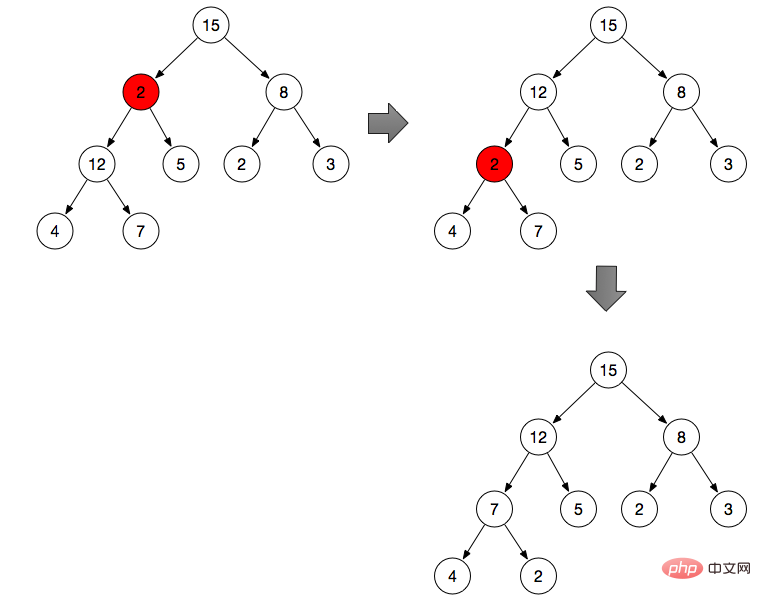
위 그림과 같이:
분기 노드 2 조정(분기 노드 2는 최대 힙의 속성을 충족하지 않음)
기본 분기 노드는 최대값입니다
2를 Branch 비교로 변경하고 2, 12, 5에서 최대값을 찾은 다음 2와 위치를 교환합니다.
위에서 언급한 바이너리 힙 속성에 따라 의 왼쪽 노드와 오른쪽 노드를 가져옵니다. Branch node 2 각각
3개의 노드를 비교하여 최대값의 첨자 max를 구합니다
노드 자체가 최대값이면 연산을 중지합니다
max 노드를 상위 노드로 교환
2, 4, 7 중 최대값을 찾아 2
Recursion
maxHeapify(i) {
let max = i;
if(i >= this.size){
return;
}
// 当前序号的左节点
const l = i * 2 + 1;
// 当前需要的右节点
const r = i * 2 + 2;
// 求当前节点与其左右节点三者中的最大值
if(l this.data[max]){
max = l;
}
if(r this.data[max]){
max = r;
}
// 最终max节点是其本身,则已经满足最大堆性质，停止操作
if(max === i) {
return;
}
// 父节点与最大值节点做交换
const t = this.data[i];
this.data[i] = this.data[max];
this.data[max] = t;
// 递归向下继续执行
return this.maxHeapify(max);
}에서 2단계의 작업을 반복합니다. 초기화된 힙은 배열로 표현되는데, 이때 최대 힙 또는 최소 힙의 속성을 만족시키기 위해서는 전체 힙을 원하는 대로 구축해야 할 수도 있습니다.
위에서 max-heapify 작업을 수행했으며, max-heapify는 특정 분기 노드만 조정합니다. 전체 힙을 최대 힙으로 구축하려면 아래와 같이 모든 분기 노드에서 max-heapify 작업을 수행해야 합니다. 4개의 분기 노드 12, 3, 2, 15에서 순서대로 max-hepify 작업을 수행해야 합니다. 시퀀스 번호 >=Math.floor(n/2)이므로 Math.floor(n/2)보다 작은 시퀀스 번호는 조정해야 하는 노드입니다.
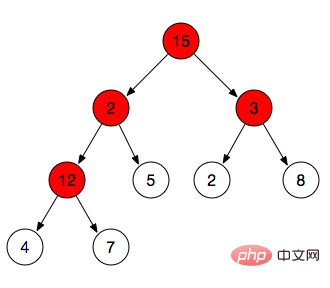예를 들어 길에 보이는 배열은 [15,2,3,12,5,2,8,4,7] => Math.floor(9/2)=4 => 인덱스는 4보다 작음 15, 2, 3, 12(조정이 필요한 노드)이고, 5, 2, 8, 4, 7은 리프 노드입니다.
rebuildHeap(){
// 叶子节点
const L = Math.floor(this.size / 2);
for(let i = L - 1; i>=0; i--){
this,maxHeapify(i);
}
}위 그림과 같이 최대 힙 정렬:
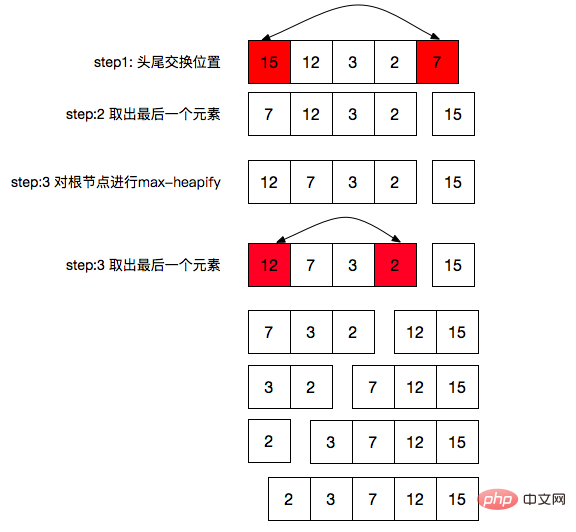will 힙에서 마지막 요소를 가져옵니다. 이는 힙의 크기인 1
sort() {
for(let i = this.size - 1; i > 0; i--){
swap(this.data, 0, i);
this.size--;
this.maxHeapify(0);
}
} insert(key) {
this.data[this.size] = key;
this.size++
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
delete(index) {
if (index >= this.size) {
return;
}
this.data.splice(index, 1);
this.size--;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}/**
* 最大堆
*/
function left(i) {
return i * 2 + 1;
}
function right(i) {
return i * 2 + 2;
}
function swap(A, i, j) {
const t = A[i];
A[i] = A[j];
A[j] = t;
}
class Heap {
constructor(arr) {
this.data = [...arr];
this.size = this.data.length;
}
/**
* 重构堆
*/
rebuildHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i--) {
this.maxHeapify(i);
}
}
isHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i++) {
const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;
const max = Math.max(this.data[i], l, r);
if (max !== this.data[i]) {
return false;
}
return true;
}
}
sort() {
for (let i = this.size - 1; i > 0; i--) {
swap(this.data, 0, i);
this.size--;
this.maxHeapify(0);
}
}
insert(key) {
this.data[this.size++] = key;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
delete(index) {
if (index >= this.size) {
return;
}
this.data.splice(index, 1);
this.size--;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
/**
* 堆的其他地方都满足性质
* 唯独跟节点，重构堆性质
* @param {*} i
*/
maxHeapify(i) {
let max = i;
if (i >= this.size) {
return;
}
// 求左右节点中较大的序号
const l = left(i);
const r = right(i);
if (l this.data[max]) {
max = l;
}
if (r this.data[max]) {
max = r;
}
// 如果当前节点最大，已经是最大堆
if (max === i) {
return;
}
swap(this.data, i, max);
// 递归向下继续执行
return this.maxHeapify(max);
}
}
module.exports = Heap;위 내용은 JavaScript의 이진 트리(이진 힙) 소개(코드 예제)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
