Python의 데이터 구조 및 알고리즘 이해: Python의 데이터 구조는 데이터 요소 간의 관계에 대한 정적 설명을 의미하며, 알고리즘은 문제를 해결하기 위한 방법 또는 단계를 의미합니다. 데이터 구조는 알고리즘이 처리해야 하는 문제의 전달자입니다.
데이터 구조와 알고리즘은 프로그램 개발자에게 필수적인 기본 기술이므로 이를 먼저 학습하고 축적해야 합니다. 다음으로 이 글에서 이 두 가지 지식 포인트를 자세히 소개하겠습니다. 모두에게 도움이 됩니다. ㅋㅋㅋ 1000 및 a2+ b2 =c^2 (a, b, c는 자연수), a, b, c의 가능한 모든 조합을 찾는 방법은 무엇입니까?
첫 번째 시도
import time
start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 1066.117884 complete!
알고리즘의 개념
알고리즘은 컴퓨터 정보 처리의 핵심입니다. 컴퓨터 프로그램은 본질적으로 지정된 작업을 수행하기 위한 정확한 단계를 컴퓨터에 알려주는 알고리즘이기 때문입니다. 일. 일반적으로 알고리즘은 정보를 처리할 때 입력 장치 또는 데이터의 저장 주소에서 데이터를 읽고 나중에 호출할 수 있도록 결과를 출력 장치 또는 저장 주소에 씁니다.알고리즘은 문제를 해결하기 위한 독립적인 방법이자 아이디어입니다.
알고리즘에서는 구현 언어가 중요한 것이 아니라 아이디어가 중요합니다.알고리즘은 다양한 언어 설명 및 구현 버전(예: C 설명, C++ 설명, Python 설명 등)을 가질 수 있습니다. 이제 Python 언어를 사용하여 이를 설명하고 구현합니다.
알고리즘의 다섯 가지 특징
입력: 알고리즘에 0개 이상의 입력이 있습니다.
출력: 알고리즘에 최소 1개 이상의 출력이 있습니다.
결정성: 알고리즘의 모든 단계는 명확한 의미를 가지며 모호성은 없습니다.
타당성: 알고리즘의 모든 단계는 실행 가능합니다. , 각 단계는 제한된 횟수만큼 실행될 수 있습니다.두 번째 시도
import time
start_time = time.time()
# 注意是两重循环
for a in range(0, 1001):
for b in range(0, 1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 0.632128
알고리즘 효율성 측정
실행 시간 반응 알고리즘 효율성동일한 문제에 대해 두 가지 해결 알고리즘을 제공했는데, 두 알고리즘의 구현에서 프로그램의 실행 시간을 측정한 결과 두 프로그램의 실행 시간이 매우 다르다는 것을 알 수 있었습니다. 결론: 알고리즘 프로그램의 실행 시간은 알고리즘의 효율성, 즉 알고리즘의 품질을 반영할 수 있습니다.
시간가치만 절대적으로 신뢰할 수 있나요?오래된 구성과 낮은 성능을 갖춘 컴퓨터에서 알고리즘에 대한 두 번째 시도를 실행하면 어떻게 될까요? 아마도 실행 시간은 컴퓨터에서 알고리즘 1을 실행하는 것보다 훨씬 빠르지 않을 것입니다.
단순히 실행 시간에만 의존하여 알고리즘의 장점을 비교하는 것은 반드시 객관적이고 정확한 것은 아닙니다!프로그램 실행은 컴퓨터 환경(하드웨어 및 운영 체제 포함)과 분리될 수 없습니다. 이러한 객관적인 이유는 프로그램 실행 속도에 영향을 미치고 프로그램 실행 시간에 반영됩니다. 그렇다면 어떻게 알고리즘의 품질을 객관적으로 판단할 수 있을까요?
시간 복잡도와 "빅오 표기법"
컴퓨터가 알고리즘의 각 기본 연산을 수행하는 데 걸리는 시간을 고정된 시간 단위라고 가정하고, 기본 연산의 횟수는 몇 시간 단위인지를 나타냅니다. 걸릴 것입니다. 정확한 단위 시간은 기계 환경마다 다르지만, 알고리즘이 수행하는 기본 작업의 수(즉, 소요되는 시간 단위의 수)는 대단위로 동일하므로 기계 환경의 영향을 받을 수 있습니다. 무시하고 객관적 반응 알고리즘의 시간 효율성. 알고리즘의 시간 효율성을 위해 "Big O 표기법"을 사용하여 표현할 수 있습니다.
"Big O 표기법": 단조 정수 함수 f에 대해 정수 함수 g와 실수 상수 c>0이 있으면 충분히 큰 n에 대해 항상 f(n)<=c*g가 됩니다. (n) , 함수 g는 f(상수 무시)의 점근 함수라고 하며 f(n)=O(g(n))으로 기록됩니다. 즉, 무한대로 향하는 극한의미에서 함수 f의 성장률은 함수 g에 의해 제약을 받는다. 즉, 함수 f와 함수 g의 특성은 유사하다.
시간 복잡도: 알고리즘 A가 크기 n의 문제 예를 처리하는 데 걸리는 시간이 T(n)=O(g(n))이고 O(g(n))인 함수 g가 있다고 가정합니다. 알고리즘 A라고 합니다. 시간 복잡도라고 하는 점근적 시간 복잡도는 T(n)으로 표시됩니다.
"Big O 표기법"을 이해하는 방법对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。
最坏时间复杂度
分析算法时，存在几种可能的考虑：
算法完成工作最少需要多少基本操作，即最优时间复杂度
算法完成工作最多需要多少基本操作，即最坏时间复杂度
算法完成工作平均需要多少基本操作，即平均时间复杂度
对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。
对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。
对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。
因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。
时间复杂度的几条基本计算规则
基本操作，即只有常数项，认为其时间复杂度为O(1)
顺序结构，时间复杂度按加法进行计算
循环结构，时间复杂度按乘法进行计算
分支结构，时间复杂度取最大值
判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度
算法分析
第一次尝试的算法核心部分
or a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))时间复杂度：
T(n) = O(n * n * n) = O(n³)
第二次尝试的算法核心部分
for a in range(0, 1001):
for b in range(0, 1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c: %d, %d, %d" % (a, b, c))时间复杂度：
T(n) = O(n * n * (1+1)) = O(n * n) = O(n²)
由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好多的。
常见时间复杂度
| 执行次数函数举例 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n + 3 | O(n) | 线性阶 |
| 3n² +2n + 1 | O(n²) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n³ +2n² +3n + 1 | O(n³) | 立方阶 |
| 2n | O(2n) | 指数阶 |
注意，经常将log2n（以2为底的对数）简写成logn
常见时间复杂度之间的关系
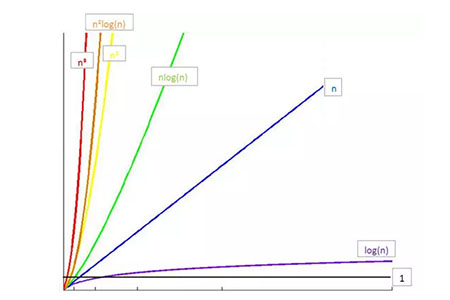
所消耗的时间从小到大
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
Python内置类型性能分析
timeit模块
timeit模块可以用来测试一小段Python代码的执行速度。
class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)
Timer是测量小段代码执行速度的类。
stmt参数是要测试的代码语句（statment）
setup参数是运行代码时需要的设置
timer参数是一个定时器函数，与平台有关。
timeit.Timer.timeit(number=1000000)
Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。
list的操作测试
def test1():
l = [] for i in range(1000):
l = l + [i]def test2():
l = [] for i in range(1000):
l.append(i)def test3():
l = [i for i in range(1000)]def test4():
l = list(range(1000))from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')pop操作测试
x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')测试pop操作：从结果可以看出，pop最后一个元素的效率远远高于pop第一个元素
可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入？？？
list内置操作的时间复杂度
dict内置操作的时间复杂度
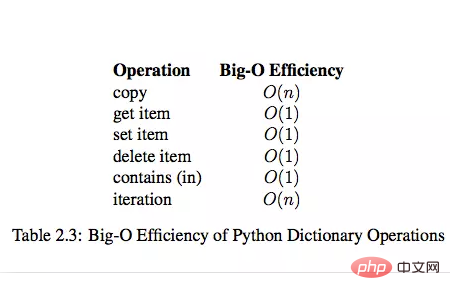
数据结构
概念
数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。
Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。
算法与数据结构的区别
数据结构只是静态的描述了数据元素之间的关系。
高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法
总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体
抽象数据类型(Abstract Data Type)
抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。
最常用的数据运算有五种
插入
删除
修改
查找
排序
위 내용은 데이터 구조와 알고리즘을 이해하는 방법(Python)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
