시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트-PHP 튜토리얼-php.cn

이 기사에서는 시간 복잡도가 무엇인지 쉽게 이해할 수 있도록 일련의 그림을 사용합니다. 흥미롭고 생생하며 관심 있는 친구는 특정 학습 가치가 있습니다. 와서 알아보세요.

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

# 🎜 🎜#

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

#🎜 🎜#

시간 복잡도의 의미

시간 복잡도란 정확히 무엇인가요? 학위는 어떻습니까? 한 장면을 상상해 보겠습니다. 어느 날 Xiao Hui와 Da Huang이 동시에 회사에 입사했습니다... Dahuang이 각각 코드를 전달했는데, 양쪽 끝에서 코드로 구현된 기능이 비슷합니다. Dahuang의 코드는 한 번 실행하는 데 100밀리초가 걸리고 5MB의 메모리를 차지합니다. Xiao Hui의 코드는 한 번 실행하는 데 100초가 걸리고 500MB의 메모리를 차지합니다. 그럼...

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

코드 품질을 측정하는 데에는 매우 두 가지가 포함된다는 것을 알 수 있습니다. 중요한 지표:

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트 1. 실행 시간

2. 시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

# 🎜 🎜# 시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

기본 연산 실행 횟수

코드의 기본 연산 실행 횟수에 대해서는, 인생의 장면에 비유해 봅시다:

장면 1: 샤오후이에게 10인치 빵을 주세요 샤오후이는 3일에 1인치씩 먹습니다. , 그렇다면 덩어리를 다 먹는 데 며칠이 걸립니까?

답은 당연히 3 X 10 = 30일입니다.

빵의 길이가 N인치라면?

이때 빵을 다 먹으려면 3 X n = 3n일이 걸립니다.

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트 이 상대적인 시간을 함수로 표현하면 T(n) = 3n으로 기록할 수 있습니다.

장면 2:

샤오후이에게 16인치 빵을 줍니다. 샤오후이는 5일마다 남은 빵 길이의 절반을 먹고, 8인치를 먹습니다. 두 번째는 4인치, 세 번째는 2인치를 먹었는데... 샤오후이가 1인치 빵만 먹는 데는 며칠이 걸릴까요?

이 질문을 번역하면 숫자 16을 계속해서 2로 나눕니다. 결과는 몇 번이나 1이 될까요? 여기에는 수학의 로그가 포함됩니다. 밑이 2인 16의 로그는 log16으로 축약될 수 있습니다.

따라서 빵 1인치를 먹는 데는 5 X log16 = 5 X 4 = 20일이 걸립니다.

빵의 길이가 N인치라면? 5 X logn = 5logn 일이 필요하며 T(n) = 5logn으로 기록됩니다.

장면 3:

샤오후이에게 10인치 빵과 닭고기 드럼스틱을 주세요. 샤오후이는 이틀에 한 번씩 드럼스틱을 먹습니다. 그렇다면 샤오후이가 닭다리를 통째로 먹는 데는 며칠이 걸릴까요?

답은 당연히 2일 입니다. 왜냐면 10인치 빵과는 전혀 상관없는 닭다리를 먹는다고만 말했으니까.

빵의 길이가 N인치라면?

빵의 길이에 관계없이 닭다리를 먹는 데 걸리는 시간은 여전히 2일로 T(n) = 2로 기록됩니다.

시나리오 4: 샤오후이에게 10인치 빵을 주세요. 샤오후이가 첫 번째 인치를 먹는 데는 1일이 걸리고, 두 번째 인치를 먹는 데는 2일이 걸리며, 세 번째 인치를 먹는 데는 3일이 걸립니다. ..1인치를 더 먹을 때마다 하루가 더 걸립니다. 그럼 샤오후이가 빵을 다 먹는 데 며칠이 걸리나요?

답은 1부터 10까지의 합으로 55일입니다.

빵의 길이가 N인치라면?

이때 빵을 통째로 먹으려면 1+2+3+......+n-1 +n = (1+n)*n/2 = 0.5n^2 + 0.5n이 필요합니다.

T(n) = 0.5n^2 + 0.5n으로 기록됩니다.

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

위에서 이야기한 것은 식사에 소요되는 상대적인 시간입니다. 이 아이디어는 프로그램의 기본 작업 횟수 통계에도 적용됩니다. 이제 네 가지 시나리오는 프로그램에서 가장 일반적인 네 가지 실행 방법에 해당합니다.

시나리오 1: T(n) = 3n, 실행 횟수는 선형입니다.

void eat1(int n){
    for(int i=0; i<n; i++){;
        System.out.println("等待一天");
        System.out.println("等待一天");
        System.out.println("吃一寸面包");
    }
}
vo

로그인 후 복사

시나리오 2: T(n) = 5logn, 실행 횟수는 로그입니다.

void eat2(int n){
   for(int i=1; i<n; i*=2){
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("吃一半面包");
   }
}

로그인 후 복사

시나리오 3: T(n) = 2, 실행 횟수는 일정합니다.

void eat3(int n){
   System.out.println("等待一天");
   System.out.println("吃一个鸡腿");
}

로그인 후 복사

시나리오 4: T(n) = 0.5n^2 + 0.5n, 실행 횟수는 다항식입니다.

void eat4(int n){
   for(int i=0; i<n; i++){
       for(int j=0; j<i; j++){
           System.out.println("等待一天");
       }
       System.out.println("吃一寸面包");
   }
}

로그인 후 복사

점근적 시간 복잡도

기본 연산 실행 횟수 T(n) 함수를 사용하면 코드의 실행 시간을 분석하고 비교할 수 있나요? ? 여전히 어려움이 있습니다.

예를 들어, 알고리즘 A의 상대 시간은 T(n) = 100n이고, 알고리즘 B의 상대 시간은 T(n) = 5n^2입니다. 둘 중 실행 시간이 더 오래 걸립니다. 이는 n 값에 따라 달라집니다.

그래서 이때 점근적 시간 복잡도(asymptotic time complexiy)라는 개념이 있습니다. 공식적인 정의는 다음과 같습니다.

함수 f(n)이 있으면 n이 무한대에 접근할 때 T( n)/f (n)의 극한값이 0이 아닌 상수인 경우, f(n)은 T(n)과 동일한 크기 차수의 함수라고 합니다.

T(n) = O(f(n))으로 설명되는 O(f(n))은 알고리즘의 점근적 시간 복잡도, 줄여서 시간 복잡도라고 합니다.

점근적 시간 복잡도는 대문자 O로 표시되므로 Big O 표기법이라고도 합니다.

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

시간 복잡도를 어떻게 도출하나요? 몇 가지 원칙이 있습니다.

실행 시간이 일정한 크기인 경우 상수 1로 표시됩니다.
시간 함수에서 가장 높은 항만 유지합니다. - 차수 항이 존재하는 경우 생략합니다. 최고 차수 항 이전의 계수입니다.
지금 바로 네 장면을 되돌아보겠습니다.

시나리오 1:

T(n) = 3n 최고차항은 3n이고 계수 3을 생략하면 변환의 시간 복잡도는 다음과 같습니다.

T(n) = O(n)

시나리오 2: 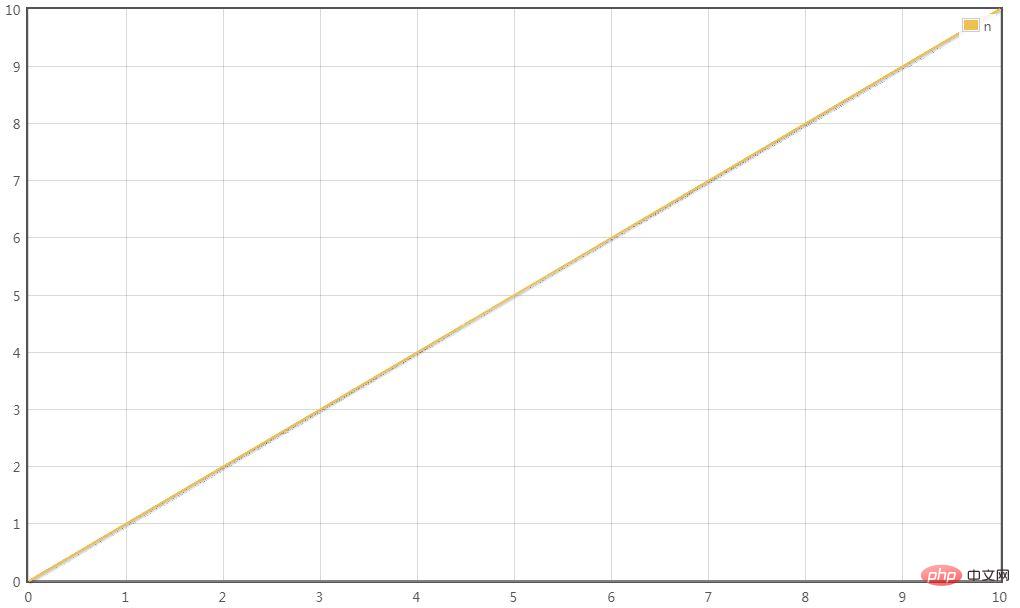시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

T(n) = 5logn 최고차 항은 5logn이고 계수 5를 생략하면 변환의 시간 복잡도는 다음과 같습니다.

T(n) = O(logn)

시나리오 3: 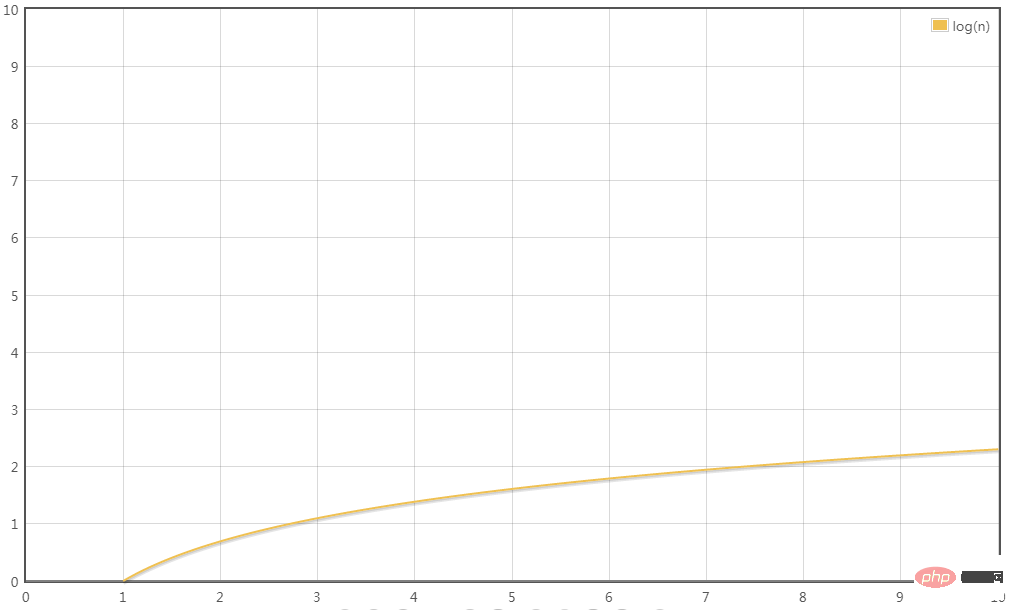시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

T(n) = 2크기만 일정하고 변환의 시간 복잡도는 다음과 같습니다.

T(n) = O(1)

시나리오 4: 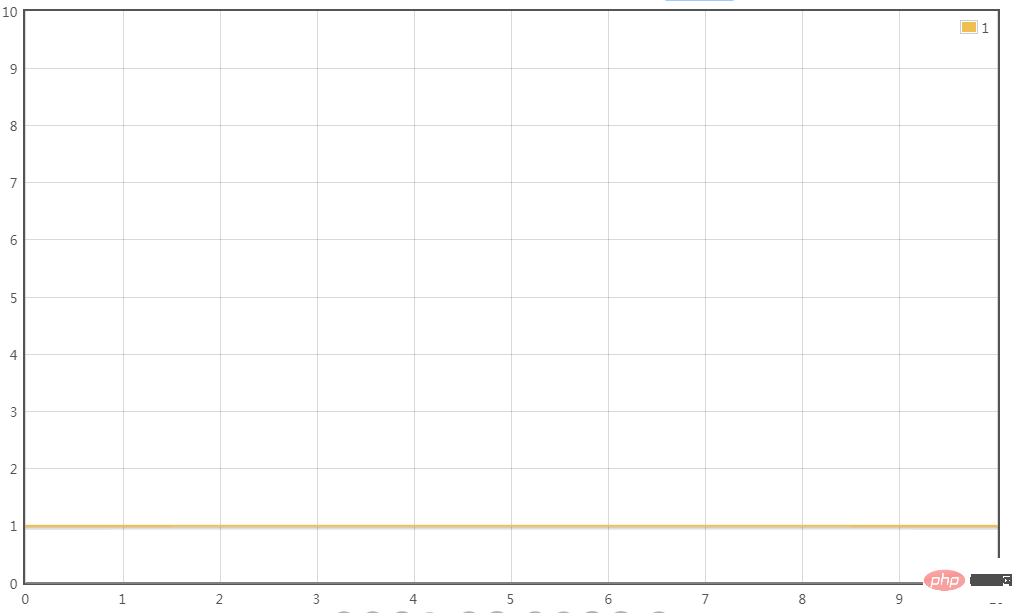시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

T(n) = 0.5n^2 + 0.5n최고차 항은 0.5n^2이며 계수 0.5를 생략하면 변환의 시간 복잡도는 다음과 같습니다.

T(n) = O(n^ 2)

이 네 가지 시간 복잡성 중 어느 것이 더 오래 걸리고 누가 시간을 절약합니까? 조금 생각해보면 다음과 같은 결론에 도달할 수 있습니다.

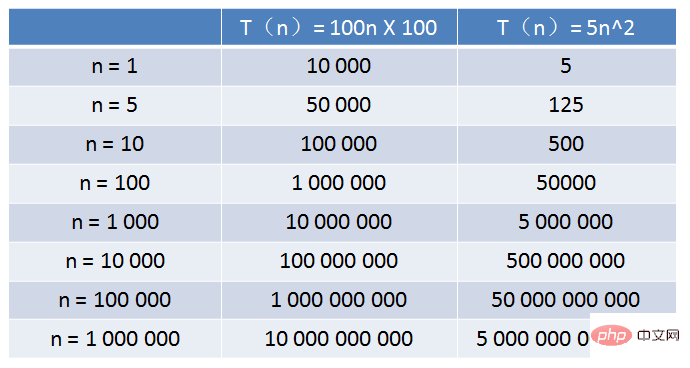
시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트 O(1)

프로그래밍 세계에는 다양한 알고리즘이 있습니다. 위의 네 가지 시나리오 외에도

O(nlogn), O(n^3), O(m*n), O(2^n), O(와 같은 다양한 형태의 시간 복잡도가 있습니다. n ! )

앞으로도 코드의 바다를 여행하다 보면 위에서 언급한 시간복잡도 알고리즘을 계속 만나게 될 것입니다.

시간복잡도의 큰 차이

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

한 마디로:

알고리즘 A의 상대적 시간 척도는 T(n) = 100n이고, 시간 복잡도는 O입니다. (n)

알고리즘 B의 상대적 시간 척도는 T(n) = 5n^2이고 시간 복잡도는 O(n^2)입니다.

알고리즘 A는 Xiao Hui의 집에 있는 오래된 컴퓨터에서 실행되고, 알고리즘 B는 특정 슈퍼컴퓨터에서 실행 속도는 기존 컴퓨터의 100배입니다.

그렇다면 입력 크기 n이 증가하면 두 알고리즘 중 어느 것이 더 빠르게 실행되나요?

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트

표에서 볼 수 있듯이 n 값이 매우 작을 때 알고리즘 A의 실행 시간은 n 값이 약 1000에 도달할 때 알고리즘 B의 실행 시간보다 훨씬 깁니다. 알고리즘 A와 알고리즘 B는 서로 가까워지고 n의 값이 10만 또는 100만개에 도달하면 알고리즘 A의 장점이 나타나기 시작하는 반면 알고리즘 B는 점점 느려지고 격차가 커집니다. 점점 더 분명해집니다.

이것은 다양한 시간 복잡성으로 인해 발생하는 차이입니다.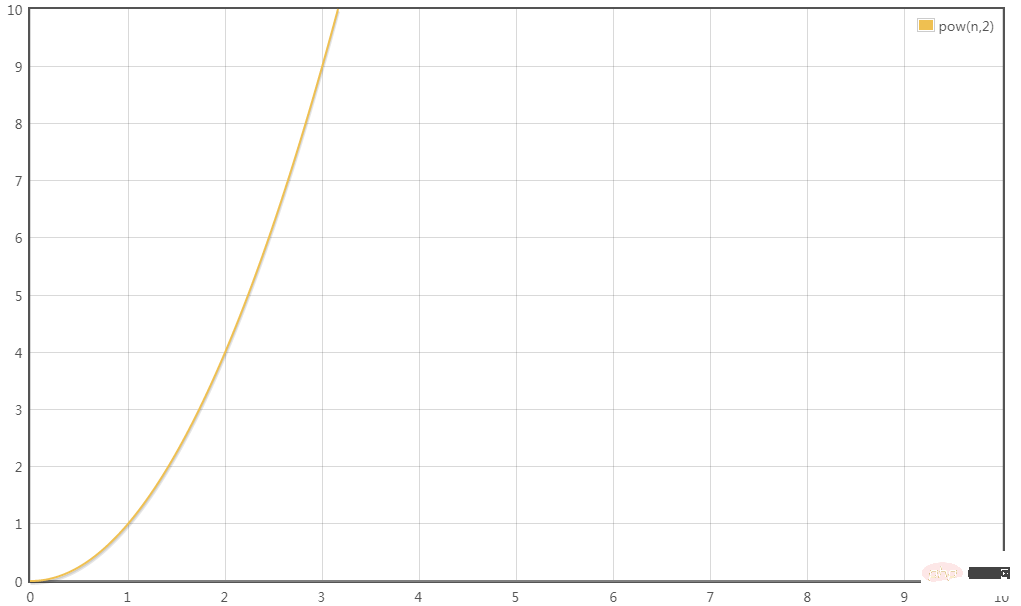

시간 복잡도를 이해하는 데 도움이 되는 데이터 구조 다이어그램 세트