내일은 메이데이인데, 여행 가이드 준비는 되셨나요? 오늘은 에디터가 다익스트라(dijkstra) 알고리즘을 활용해 저렴하고 걱정 없이 여행 경로를 쉽게 찾는 방법에 대한 기사를 소개하겠습니다.
사례:
5월이 곧 다가오고 Xiao Zhang은 여행을 떠날 준비가 되었습니다!
여러 곳에서 항공권을 확인했어요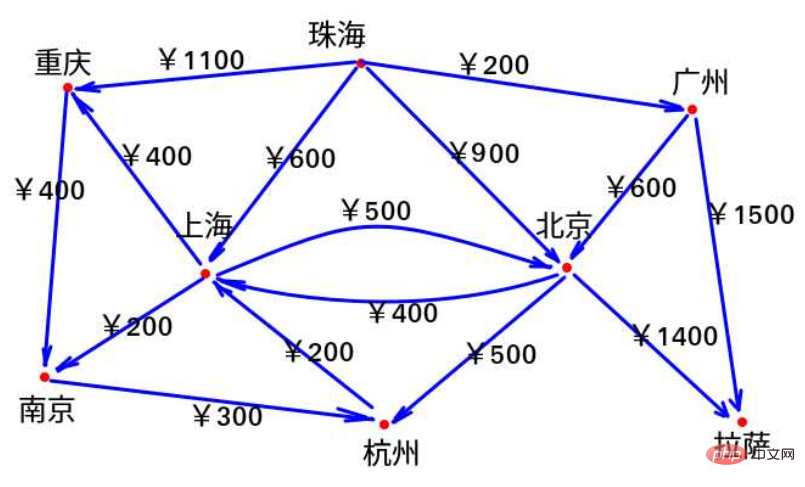
올해 월급이 많이 깎여서 장샤오 씨는 돈이 별로 없어서 예산 관리에 주의해야 해요. 그는 여러 도시에 가는 데 드는 비용이 가장 저렴한지 알아보고 싶어합니다.
【글쎄, 돌아오는 데 드는 비용을 고려할 필요는 없습니다. Xiao Zhang은 경찰 삼촌에게 자신이 납치되었다는 사실을 알리고 무료로 돌려보내려고 했습니다. ]
주하이에서 라사까지 비행기를 타고 가고 싶다면 최소 항공권 비용은 얼마인가요? 오늘 이야기할 알고리즘에 대해 이야기해보겠습니다.
Dijkstra 알고리즘은 일반적인 단일 소스 최단 경로 알고리즘으로, 한 노드에서 다른 모든 노드까지의 최단 경로를 계산하는 데 사용됩니다. 주요 특징은 시작점부터 끝점에 도달할 때까지 한 겹씩 바깥쪽으로 확장된다는 점입니다. Dijkstra 알고리즘의 시간 복잡도는 O(N^2)입니다.
Dijkstra는 1930년 5월 11일 네덜란드 로테르담의 지식인 가정에서 태어났습니다. 그녀는 네 형제 자매 중 세 번째였습니다. 그의 아버지는 네덜란드 화학 협회의 회장을 역임한 화학자이자 발명가였습니다. 그의 어머니는 수학자이다. 그는 장애물이 있는 두 위치 사이의 최단 경로를 찾는 효율적인 알고리즘을 성공적으로 설계하고 구현했습니다. 이 알고리즘은 "Dijkstra 알고리즘"으로 명명되었으며 로봇 공학의 매우 중요한 문제, 즉 동작 경로 계획 문제를 해결했습니다. 오늘.
관련 튜토리얼: 데이터 구조 모험 사진
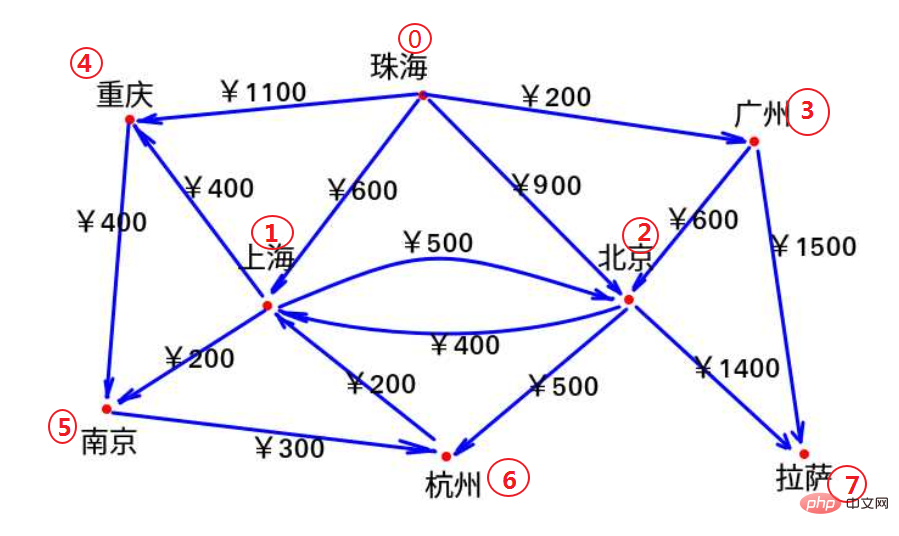
주하이와 직접 연결된 도시에는 상하이, 베이징, 광저우, 충칭이 포함됩니다. 주하이에서 다른 도시까지의 항공권 가격은 다음과 같습니다(직접 연결이 없는 경우 무한대로 표시됩니다). 이 4개 도시 중 광저우가 가격이 가장 저렴하므로 광저우에서 환승하겠습니다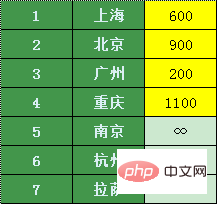
항공권이 가장 저렴한 광저우에서 환승
비교해보면 주하이에서 광저우까지 200위안, 광저우에서 베이징까지 600위안입니다. . 총 800 위안입니다 (시간이 낭비 될 수도 있고, Xiao Zhang은 가난하고 시간 만 남았습니다)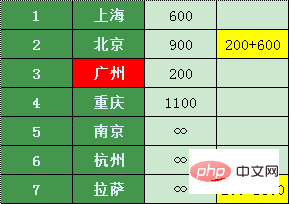 
광주에서 라사로 환승 1700 위안, 그러면 확실히 Da Dao보다 낫지 않습니다.
광저우 외에 연결편이 가장 저렴한 도시인 상하이를 찾아보자 - 상하이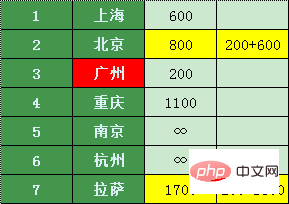 
원래 가격과 비교해 보니 상하이에서 충칭, 난징으로 환승하는 것이 더 저렴한 것으로 나타났습니다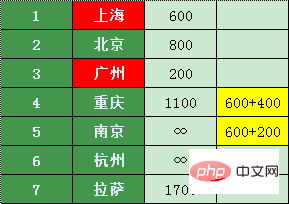 
광저우와 상하이를 제외하고 가장 저렴한 환승 도시를 찾아보자 - 베이징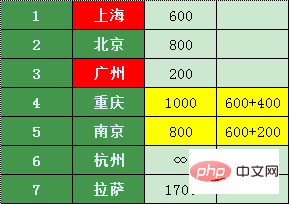 
라사 가격은 베이징 최저가입니다. 800 + 베이징 -> 라싸 1400(2200)의 가격 합이 더 높음 1700에서 항저우 800 + 500 = 1300, 최저 가격표는 다음과 같습니다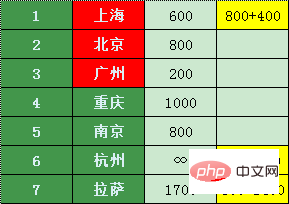
난징은 항저우로만 직항만 갈 수 있는데,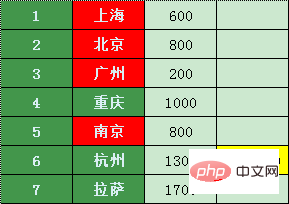 
난징에서 항저우까지의 가격은 1100인데 가격이 착하다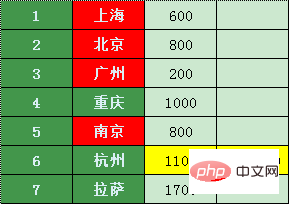
충칭에서 직접 연결되는 유일한 노선은 난징이며, 난징까지 가는 데 비용은 1000 + 400 = 1400위안입니다. 난징까지의 원래 800 위안과 비교하면 확실히 비용 효율적이지 않습니다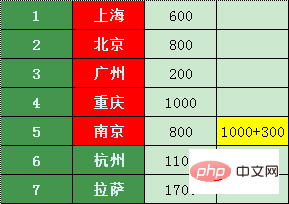 
항저우 만 갈 수 있습니다 상하이 행, 가격은 상하이보다 높습니다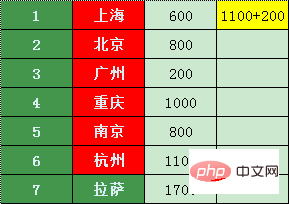 
그러면 라사 행 가장 저렴한 항공권은 1,700 위안입니다.
1) 0,1,2,...,7을 사용하여 각각 주하이, 상하이, 베이징, 광저우, 충칭, 난징, 항저우, 라사를 나타냅니다.
2) 2차원 배열 가격[8][8]을 사용하여 항공편 가격을 나타냅니다. 가격[i][j] = i에서 j까지의 직항 항공편 가격(항공편이 없는 경우 로 기록)
3 ) minPrice 배열을 사용하여 주하이에서 다양한 도시까지의 최소 항공권 비용을 기록하려면:
4) 배열 플래그를 사용하여 도시가 연결되었는지 표시합니다.
// 表示无穷大 即不可达
public static int NO_AIRPLANE = Integer.MAX_VALUE;
// 初始直飞价格表
public int[][] prices ;
// 最优转机价格表
public int[] minPrice ;
public boolean[] flag ;
private int citySize; public static int[][] getPrices(){
int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS = 7;
int[][] prices = new int[8][8];
//from Zhuhai
prices[ZH][CQ] = 1100;
prices[ZH][SH] = 600;
prices[ZH][BJ] = 900;
prices[ZH][GZ] = 200;
//others
prices[CQ][NJ] = 400;
prices[SH][CQ] = 400;
prices[SH][BJ] = 500;
prices[SH][NJ] = 200;
prices[BJ][SH] = 400;
prices[BJ][HZ] = 500 ;
prices[BJ][LS] = 1400;
prices[GZ][BJ] = 600 ;
prices[GZ][LS] = 1500 ;
prices[NJ][HZ] = 300 ;
prices[HZ][SH] = 200 ;
for(int i = 0 ; i < 8 ; i++){
for(int j = 0 ; j < 8 ; j++){
if(prices[i][j] == 0){
prices[i][j] = NO_AIRPLANE;
}
}
}
return prices;
}// 初始化始发站价格表
for(int i = 1; i < citySize;i++){
minPrice[i-1] = prices[0][i];
}private void dijkstra(){
int min = Integer.MAX_VALUE;
int minIdx = Integer.MAX_VALUE;
// 找到最小的价格
for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
if(!flag[idx] && minPrice[idx] < min ){
min = minPrice[idx];
minIdx = idx ;
}
}
if(minIdx == Integer.MAX_VALUE){
// 已经没有最小的了
return ;
}
//标记从该城市转机
flag[minIdx] = true;
minIdx += 1;
System.out.println("最小城市序号"+minIdx +" 价格"+ minPrice[minIdx -1]);
// 获取当前城市的价格表
int cityPrice = minPrice[minIdx -1];
int[] minCityPrices = prices[minIdx];
for(int idx = 1 ; idx < citySize ; idx ++ ){
int price = minCityPrices[idx];
// 如果从杭州到达该城市的价格 加上 idx城市转机的价格 低于 从杭州到达idx城市的价格 则更新
if(!flag[idx -1 ] && price != NO_AIRPLANE && (cityPrice+ price) < minPrice[idx - 1]){
// 可达的城市到达的
minPrice[idx - 1] = cityPrice+ price;
System.out.println(idx+"更新最优表：" + Arrays.toString(minPrice));
}
}
dijkstra();
} 
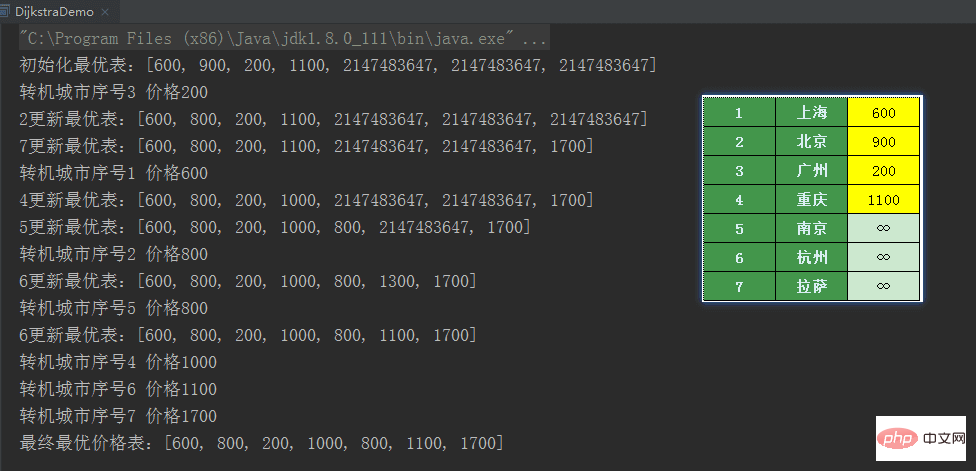
위의 푸시 과정과 동일합니다. 이 글이 도움이 되길 바랍니다.
첨부-소스코드:
package a;
import java.util.Arrays;
/**
* ┏┓ ┏┓+ +
* ┏┛┻━━━┛┻┓ + +
* ┃ ┃
* ┃ ━ ┃ ++ + + +
* ████━████ ┃+
* ┃ ┃ +
* ┃ ┻ ┃
* ┃ ┃ + +
* ┗━┓ ┏━┛
* ┃ ┃
* ┃ ┃ + + + +
* ┃ ┃ Code is far away from bug with the animal protecting
* ┃ ┃ + 神兽保佑,代码无bug
* ┃ ┃
* ┃ ┃ +
* ┃ ┗━━━┓ + +
* ┃ ┣┓
* ┃ ┏┛
* ┗┓┓┏━┳┓┏┛ + + + +
* ┃┫┫ ┃┫┫
* ┗┻┛ ┗┻┛+ + + +
*
* @Author:Halburt
* @Date:2019-04-24 下午 5:47
* @Description:
*/
public class DijkstraDemo {
// 表示无穷大 即不可达
public static int NO_AIRPLANE = Integer.MAX_VALUE;
// 初始直飞价格表
public int[][] prices ;
// 最优转机价格表
public int[] minPrice ;
public boolean[] flag ;
private int citySize;
/**
* @param citySize 城市数量
*/
public DijkstraDemo(int citySize){
this.citySize = citySize;
// prices = new int [citySize][citySize];
flag = new boolean [citySize - 1];
minPrice = new int[citySize - 1 ];
}
public static int[][] getPrices(){
int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS = 7;
int[][] prices = new int[8][8];
//from Zhuhai
prices[ZH][CQ] = 1100;
prices[ZH][SH] = 600;
prices[ZH][BJ] = 900;
prices[ZH][GZ] = 200;
//others
prices[CQ][NJ] = 400;
prices[SH][CQ] = 400;
prices[SH][BJ] = 500;
prices[SH][NJ] = 200;
prices[BJ][SH] = 400;
prices[BJ][HZ] = 500 ;
prices[BJ][LS] = 1400;
prices[GZ][BJ] = 600 ;
prices[GZ][LS] = 1500 ;
prices[NJ][HZ] = 300 ;
prices[HZ][SH] = 200 ;
for(int i = 0 ; i < 8 ; i++){
for(int j = 0 ; j < 8 ; j++){
if(prices[i][j] == 0){
prices[i][j] = NO_AIRPLANE;
}
}
}
return prices;
}
public static void main(String[] args) {
DijkstraDemo demo = new DijkstraDemo(8);
demo.dijkstra(getPrices());
}
public void dijkstra(int[][] prices ){
this.prices = prices;
// 初始化
// 初始化始发站价格表
for(int i = 1; i < citySize;i++){
minPrice[i-1] = prices[0][i];
}
System.out.println("初始化最优表：" + Arrays.toString(minPrice));
dijkstra();
System.out.println("最终最优价格表：" + Arrays.toString(minPrice));
}
private void dijkstra(){
int min = Integer.MAX_VALUE;
int minIdx = Integer.MAX_VALUE;
// 找到最小的价格
for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
if(!flag[idx] && minPrice[idx] < min ){
min = minPrice[idx];
minIdx = idx ;
}
}//=已经没有最小的了
if(minIdx == Integer.MAX_VALUE){
return ;
}
//标记从该城市转机
flag[minIdx] = true;
minIdx += 1;
System.out.println("转机城市序号"+minIdx +" 价格"+ minPrice[minIdx -1]);
//获取该城市转机时飞往其他城市的价格表
int cityPrice = minPrice[minIdx -1];
//获取杭州飞往该城市的价格
int[] minCityPrices = prices[minIdx];
for(int idx = 1 ; idx < citySize ; idx ++ ){
int price = minCityPrices[idx];
// 如果从杭州到达该城市的价格 加上 idx城市转机的价格 低于 从杭州到达idx城市的价格 则更新
if(!flag[idx -1 ] && price != NO_AIRPLANE && (cityPrice+ price) < minPrice[idx - 1]){
// 可达的城市到达的
minPrice[idx - 1] = cityPrice+ price;
System.out.println(idx+"更新最优表：" + Arrays.toString(minPrice));
}
}
dijkstra();
}
}원작자 Halburt에게 감사드립니다. 원주소: https://www.cnblogs.com/Halburt/p/10767389.html
위 내용은 Dijkstra의 알고리즘을 사용하여 노동절에 가장 경제적인 여행 경로를 찾는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
