C 언어로 최소 스패닝 트리 구현-C#.Net 튜토리얼-php.cn

C 언어로 최소 스패닝 트리 구현

angryTom

풀어 주다： 2019-11-29 15:24:04

앞으로

3717명이 탐색했습니다.

1. 최소 스패닝 트리 소개

최소란 무엇입니까? 스패닝 트리 트리?

최소 스패닝 트리(MST)는 주어진 무방향 그래프 G(V,E)에서 트리 T를 찾는 것입니다. 이 트리는 그래프 G 꼭지점의 모든 요소를 가지며 모든 가장자리는 다음과 같습니다. 그래프 G의 간선으로부터 전체 트리의 간선 가중치의 최소 합을 만족합니다.

2.prim 알고리즘

은 Dijkstra의 알고리즘과 매우 유사합니다! ! 다음 Gif 다이어그램을 참조하세요. prim 알고리즘의 핵심 아이디어는 그래프 G(V, E)에 대해 집합 S를 설정하고 방문한 정점을 저장한 다음 그래프에서 가장 짧은 거리가 가장 짧은 정점을 선택하는 것입니다. 세트 V-S(u로 표시)에서 매번 세트 S를 설정하고 세트 S에 액세스하고 참여합니다. 그런 다음 정점 u를 중간점으로 두고 u와 집합 s에서 도달할 수 있는 모든 정점 v 사이의 최단 거리를 최적화합니다. 이 작업은 집합 s에 모든 정점이 포함될 때까지 n번 수행됩니다.

C 언어로 최소 스패닝 트리 구현

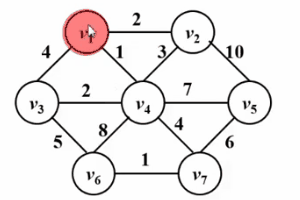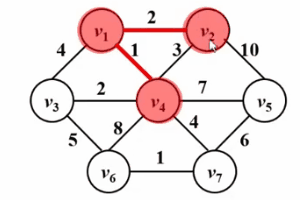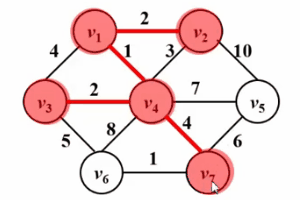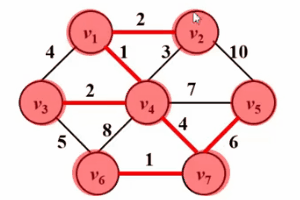
차이점은 Dijkstra 알고리즘의 dist가 소스 점 s에서 정점 w까지의 최단 경로인 반면 prim의 알고리즘의 dist는 집합 The에서 나온 것입니다. S에서 정점 w까지의 최단 경로는 Dijkstra 알고리즘에 대한 자세한 설명을 비교한 것입니다.

C 언어로 최소 스패닝 트리 구현

#🎜🎜 #알고리즘 구현: # 🎜🎜#

#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集 
int dist[MaxVertex]; // 距离 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
vector<Vertex> MST;  // 最小生成树 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图 
        dist[i] = INF;   // 初始化距离
        parent[i] = -1;  // 初始化并查集 
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        G[v1][v2] = w;
        G[v2][v1] = w;
    }
}
// Prim算法前的初始化 
void IniPrim(Vertex s){
    dist[s] = 0;
    MST.push_back(s);
    for(Vertex i =1;i<=Nv;i++)
        if(G[s][i]){
            dist[i] = G[s][i];
            parent[i] = s;
        } 
}
// 查找未收录中dist最小的点 
Vertex FindMin(){
    int min = INF;
    Vertex xb = -1;
    for(Vertex i=1;i<=Nv;i++)
        if(dist[i] && dist[i] < min){ 
            min = dist[i];
            xb = i;
        }
    return xb;
}
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<MST[i]<<" ";
    cout<<"权重和为："<<sum<<endl; 
    cout<<"该生成树为："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
}
void Prim(Vertex s){
    IniPrim(s);
    while(1){
        Vertex v = FindMin();
        if(v == -1)
            break;
        sum += dist[v];
        dist[v] = 0;
        MST.push_back(v);
        for(Vertex w=1;w<=Nv;w++)
            if(G[v][w] && dist[w])
                if(G[v][w] < dist[w]){
                    dist[w] = G[v][w];
                    parent[w] = v;
                }
    }
}
int main(){
    build();
    Prim(1);
    output();
    return 0;
}

로그인 후 복사

프림 알고리즘에 대한 자세한 설명은 영상을 참고해주세요 https://www.bilibili.com/video/av55114968?p=99

# 🎜🎜#

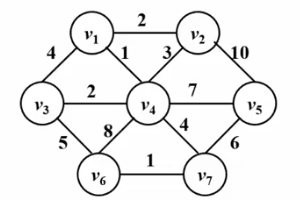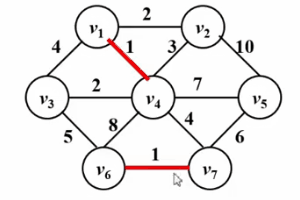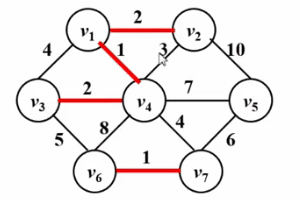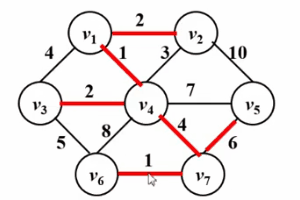
3.kruskal Algorithm

Kruskal 알고리즘은 최소 스패닝 트리 문제를 해결하는 데에도 사용할 수 있습니다. 알고리즘 아이디어는 이해하기 쉽습니다. 그리디의 알고리즘 아이디어는 다음과 같습니다. #🎜🎜 #● 초기 상태에서는 그래프의 모든 모서리가 숨겨져 있으므로 그래프의 각 꼭지점은 총 n개의 연결된 블록입니다.

● 모든 가장자리의 가장자리 가중치를 작은 것부터 작은 것까지 누릅니다. 가장 큰 것부터 큰 것 순으로 정렬합니다.

● 두 정점의 경우 작은 것부터 큰 것까지 모든 가장자리를 테스트합니다. 현재 테스트 에지에 의해 연결된 것이 동일한 연결된 블록에 없으면 이 테스트 에지를 트리의 현재 최소 생성에 추가합니다. 그렇지 않으면 해당 에지가 삭제됩니다.

● 최소 스패닝 트리의 가장자리 수가 총 정점 수에서 1을 뺀 값과 같거나 모든 가장자리가 테스트되면 종료될 때까지 이전 단계를 반복합니다. 최소 스패닝 트리의 간선은 정점의 총 개수보다 적습니다. 점에서 1을 뺀 개수는 그래프가 연결되어 있지 않음을 나타냅니다.

아래 GIF를 확인해주세요!

알고리즘 구현:

#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集最小生成树 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
struct Node{
    Vertex v1;
    Vertex v2;
    int weight; // 权重 
    // 重载运算符成最大堆 
    bool operator < (const Node &a) const
    {
        return weight>a.weight;
    }
};
vector<Node> MST;  // 最小生成树 
priority_queue<Node> q;   // 最小堆 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图
        parent[i] = -1;
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        struct Node tmpE;
        tmpE.v1 = v1;
        tmpE.v2 = v2;
        tmpE.weight = w;
        q.push(tmpE); 
    }
}
//  路径压缩查找 
int Find(int x){
    if(parent[x] < 0)
        return x;
    else
        return parent[x] = Find(parent[x]);
} 
//  按秩归并 
void Union(int x1,int x2){
    if(parent[x1] < parent[x2]){
        parent[x1] += parent[x2];
        parent[x2] = x1;
    }else{
        parent[x2] += parent[x1];
        parent[x1] = x2;
    }
} 
void Kruskal(){
    // 最小生成树的边不到 Nv-1 条且还有边 
    while(MST.size()!= Nv-1 && !q.empty()){
        Node E = q.top();  // 从最小堆取出一条权重最小的边
        q.pop(); // 出队这条边 
        if(Find(E.v1) != Find(E.v2)){  // 检测两条边是否在同一集合 
            sum += E.weight; 
            Union(E.v1,E.v2);     // 并起来 
            MST.push_back(E);
        }
    }
    
} 
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=0;i<Nv;i++)
        cout<<MST[i].weight<<" ";
    cout<<"权重和为："<<sum<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
    cout<<endl;
}
int main(){
    build();
    Kruskal();
    output();
    return 0;
}

로그인 후 복사

크루스칼 알고리즘에 대한 자세한 설명은 영상을 참고해주세요 https:/ /www.bilibili.com/video/av55114968?p=100