파이썬 정렬 알고리즘은 무엇인가요? 다음 기사에서는 Python의 상위 10가지 고전 정렬 알고리즘을 소개합니다. 도움이 필요한 친구들이 모두 참고할 수 있기를 바랍니다.
이제 프로그래밍에서 알고리즘은 매우 중요한 역할을 합니다. 알고리즘을 함수로 캡슐화하면 반복해서 작성할 필요 없이 프로그램을 더 잘 호출할 수 있습니다.
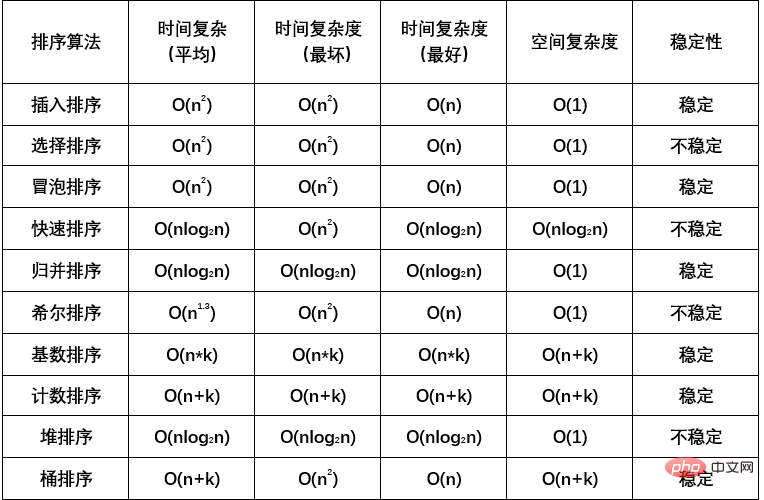
Python의 10대 클래식 알고리즘:
1. 삽입 정렬
1. 알고리즘 아이디어
두 번째 요소부터 시작하여 비교합니다. 이전 요소인 경우 이전 요소 요소가 현재 요소보다 크면 이전 요소를 뒤로 이동하고 현재 요소는 그보다 작거나 같은 요소가 발견되어 그 뒤에 삽입될 때까지 순서대로 앞으로 이동합니다.
그런 다음 세 번째 요소를 선택하고, 위의 작업을 반복하고 삽입하고 마지막 요소를 순서대로 선택하면 삽입 후 모든 정렬이 완료됩니다.
2. 코드 구현
def insertion_sort(arr):
#插入排序
# 第一层for表示循环插入的遍数
for i in range(1, len(arr)):
# 设置当前需要插入的元素
current = arr[i]
# 与当前元素比较的比较元素
pre_index = i - 1
while pre_index >= 0 and arr[pre_index] > current:
# 当比较元素大于当前元素则把比较元素后移
arr[pre_index + 1] = arr[pre_index]
# 往前选择下一个比较元素
pre_index -= 1
# 当比较元素小于当前元素，则将当前元素插入在 其后面
arr[pre_index + 1] = current
return arr2. 선택 정렬
첫 번째 요소를 비교 요소로 두고 다음 요소와 차례로 비교하여 모두 찾습니다. 가장 작은 요소를 첫 번째 요소와 교환하고, 위의 작업을 반복하고, 두 번째로 작은 요소를 찾아 두 번째 위치의 요소와 교환하는 식으로 나머지 가장 작은 요소를 찾아 교환합니다. 즉, 정렬이 완료된 것입니다.
2. 코드 구현
def selection_sort(arr):
#选择排序
# 第一层for表示循环选择的遍数
for i in range(len(arr) - 1):
# 将起始元素设为最小元素
min_index = i
# 第二层for表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
# 如果当前元素比最小元素小，则把当前元素角标记为最小元素角标
min_index = j
# 查找一遍后将最小元素与起始元素互换
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr첫 번째와 두 번째를 비교하고 첫 번째가 두 번째보다 크면 위치를 바꿉니다. 그런 다음 두 번째와 세 번째 요소를 비교합니다. 점차적으로 첫 번째 라운드 이후 가장 큰 요소가 마지막에 순위가 지정되었습니다.
따라서 위 작업이 반복되면 두 번째로 큰 요소가 마지막 위치에서 두 번째 순위가 됩니다. , 그런 다음 위 작업을 n-1번 반복하여 정렬을 완료합니다. 왜냐하면 마지막에는 요소가 하나만 있으므로 비교가 필요하지 않기 때문입니다.2. 코드 구현
def bubble_sort(arr):
#冒泡排序
# 第一层for表示循环的遍数
for i in range(len(arr) - 1):
# 第二层for表示具体比较哪两个元素
for j in range(len(arr) - 1 - i):
if arr[j] > arr[j + 1]:
# 如果前面的大于后面的，则交换这两个元素的位置
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr1. 알고리즘 아이디어 최대한 단순해야 하며 지속적으로 분해(또는 축소)되어야 합니다. 문제 규모) 기준 조건이 충족될 때까지.
2. 코드 구현
def quick_sort(arr):
if len(arr) < 2:
# 基线条件：为空或只包含一个元素的数组是“有序”的
return arr
else:
# 递归条件
pivot = arr[0]
# 由所有小于基准值的元素组成的子数组
less = [i for i in arr[1:] if i <= pivot]
# 由所有大于基准值的元素组成的子数组
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quick_sort([10, 5, 2, 3]))1. 알고리즘 아이디어병합 정렬은 분할 정복 방법의 전형적인 응용입니다. 분할 정복 방법(pide-and-Conquer): 원래 문제를 원래 문제와 유사한 구조를 갖는 n개의 더 작은 하위 문제로 나누고 이러한 문제를 재귀적으로 해결한 다음 결과를 결합하여 원래 문제에 대한 해를 얻습니다. 문제. 분해된 시퀀스는 이진 트리처럼 보입니다.
구체적인 구현 단계:재귀를 사용하여 이분법을 사용하여 소스 시퀀스를 여러 하위 열로 나눕니다. 공간을 적용하고 두 하위 열을 정렬 및 병합한 다음 반환합니다.
참고: 먼저 분해한 다음 병합합니다
2. 코드 구현
def merge_sort(arr):
#归并排序
if len(arr) == 1:
return arr
# 使用二分法将数列分两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
#排序合并两个数列
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值，直接添加
result += left
result += right
return result1. Hill 정렬의 전체적인 아이디어는 여러 요소를 고정된 간격으로 나누어 정렬한 다음 이 간격을 좁히는 것입니다. 이런 식으로 최종 시퀀스는 기본 순서 시퀀스가 됩니다. 특정 단계:
증분(간격) 값 계산
요소를 증분과 비교합니다. 예를 들어 증분 값이 7이면 0, 7, 14, 21... 요소 삽입을 수행합니다. sort2. 코드 구현
def shell_sort(arr):
#希尔排序
# 取整计算增量（间隔）值
gap = len(arr) // 2
while gap > 0:
# 从增量值开始遍历比较
for i in range(gap, len(arr)):
j = i
current = arr[i]
# 元素与他同列的前面的每个元素比较，如果比前面的小则互换
while j - gap >= 0 and current < arr[j - gap]:
arr[j] = arr[j - gap]
j -= gap
arr[j] = current
# 缩小增量（间隔）值
gap //= 2
return arr1. 알고리즘 아이디어
Radix 정렬은 "버킷 정렬" 또는 bin 정렬이라고도 하는 "분포 정렬"입니다. 이름에서 알 수 있듯이 요소는 특정 "버킷"에 할당됩니다. 기수 정렬 방법은 안정적인 정렬이며 시간 복잡도는 O(nlog(r)m)입니다. 여기서 r은 채택된 기수이고 m은 특정 시점의 힙 수입니다. 정렬 방법은 다른 안정성 정렬 방법보다 효율적입니다. 2. 코드 구현
2.1은 버킷 정렬에서 최하위 비트에서 최상위 비트로 버킷 정렬을 변환하여 최종 순위 목록을 출력합니다.
def RadixSort(list,d):
for k in range(d):#d轮排序
# 每一轮生成10个列表
s=[[] for i in range(10)]#因为每一位数字都是0~9，故建立10个桶
for i in list:
# 按第k位放入到桶中
s[i//(10**k)%10].append(i)
# 按当前桶的顺序重排列表
list=[j for i in s for j in i]
return listfrom random import randint
def radix_sort():
A = [randint(1, 99999999) for _ in xrange(9999)]
for k in xrange(8):
S = [ [] for _ in xrange(10)]
for j in A:
S[j / (10 ** k) % 10].append(j)
A = [a for b in S for a in b]
for i in A:
print i八、计数排序
1.算法思想
对每一个输入元素x，确定小于x的元素个数。利用这一信息，就可以直接把x 放在它在输出数组上的位置上了，运行时间为O(n)，但其需要的空间不一定，空间浪费大。
2.代码实现
from numpy.random import randint
def Conuting_Sort(A):
k = max(A) # A的最大值，用于确定C的长度
C = [0]*(k+1) # 通过下表索引，临时存放A的数据
B = (len(A))*[0] # 存放A排序完成后的数组
for i in range(0, len(A)):
C[A[i]] += 1 # 记录A有哪些数字，值为A[i]的共有几个
for i in range(1, k+1):
C[i] += C[i-1] # A中小于i的数字个数为C[i]
for i in range(len(A)-1, -1, -1):
B[C[A[i]]-1] = A[i] # C[A[i]]的值即为A[i]的值在A中的次序
C[A[i]] -= 1 # 每插入一个A[i]，则C[A[i]]减一
return B九、堆排序
1.算法思想
堆分为最大堆和最小堆，是完全二叉树。堆排序就是把堆顶的最大数取出，将剩余的堆继续调整为最大堆,具体过程在第二块有介绍，以递归实现 ，
剩余部分调整为最大堆后,再次将堆顶的最大数取出，再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。
2.代码实现
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)十、桶排序
1.算法思想
为了节省空间和时间，我们需要指定要排序的数据中最小以及最大的数字的值，来方便桶排序算法的运算。
2.代码实现
#桶排序
def bucket_sort(the_list):
#设置全为0的数组
all_list = [0 for i in range(100)]
last_list = []
for v in the_list:
all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
for i,t_v in enumerate(all_list):
if t_v != 0:
for j in range(t_v):
last_list.append(i)
return last_list总结：
在编程中，算法都是相通的，算法重在算法思想，相当于将一道数学上的应用题的每个条件，区间，可能出现的结果进行分解，分步骤的实现它。算法就是将具体问题的共性抽象出来，将步骤用编程语言来实现。通过这次对排序算法的整理，加深了对各算法的了解，具体的代码是无法记忆的，通过对算法思想的理解，根据伪代码来实现具体算法的编程，才是真正了解算法。
推荐学习：Python视频教程
위 내용은 파이썬 정렬 알고리즘은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
