기술의 파도가 끝없이 몰아치고 있는데, 그 파도가 물러가고 나면 우리에게 남는 것은 방법론일까요? 아니면 오래된 기술인가요?
------
우리 프로그래머들은 소위 '35세 저주'가 마치 프로그래머들의 특허가 된 것처럼 늘 이야기하기를 좋아합니다. 그러나 사실 35세라는 나이는 각계각층의 전문가들이 직면하는 문제이다.
기본적으로 35세는 중년이 되는 전환점입니다. 직장에서 우리의 가치관이 체력에 더 많이 의존한다면 우리는 경력 개발의 딜레마에 직면하게 될 것입니다.
프로그래밍은 원래 추상적인 사고와 논리적 추론을 중시하는 매우 창의적인 작업이지만, 프로그래밍을 물처럼 일상적인 일처럼 취급하는 사람들이 꽤 있습니다. 저주'는 우리를 괴롭히게 될 것입니다.
사회 집단에서는 사람마다 선택이 다릅니다. 나는 의도도 없고 일반적인 환경을 바꿀 수도 없지만, "35세의 저주"에 맞서 싸우려는 프로그래머들이 방향을 찾고 작업할 수 있도록 돕고 싶습니다. 몇 년 더!
양희삼각형은 제가 면접에서 자주 받는 질문입니다. "양희삼각형의 첫 N줄을 지정된 형식에 맞게 프로그램해서 출력해주세요."
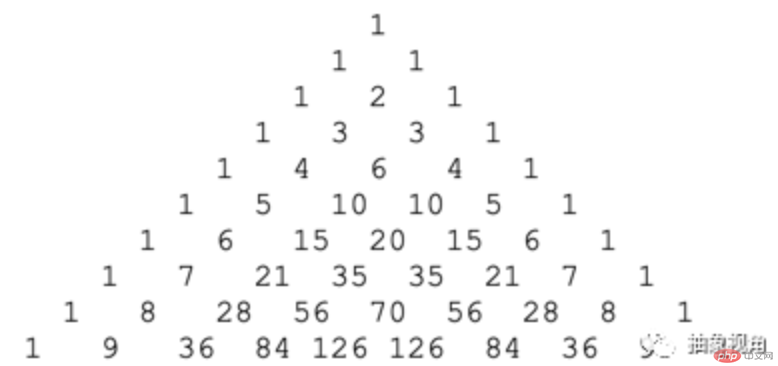
대부분의 지원자들은 질문을 받고 코딩을 시작했습니다. 그들은 먼저 2계층 루프를 작성했고, 그다음 루프의 종료 조건에 대해 생각하기 시작했습니다. . 가장 인상적인 경우 중 하나는 WeChat Pay의 후보자가 처음 N 행의 데이터를 얻는 방법만 제공했지만 여전히 지정된 형식으로 인쇄하는 방법을 찾지 못한 경우였습니다.
학교를 떠난 지 몇 년이 지나서 알고리즘을 잊어버렸다고 말하는 사람이 많을 것입니다. 학교에서 모집하는 학생들에게 이런 질문을 던져야 합니다. 제가 관심을 두는 것은 특정 알고리즘이 아니라 문제를 분석하고 해결하는 아이디어입니다. 특정 알고리즘을 잊어버릴 수도 있지만, 잊어버리는 동안 알고리즘에 담긴 문제 해결 아이디어를 우리 자신의 무기로 내면화해야 합니다.
다음으로, 이 문제를 어떻게 보는지 소개하겠습니다.
Turing Award 수상자 N. Wirth는 "프로그램 = 알고리즘 + 데이터 구조"를 제안했는데, 저는 "프로그램 = 데이터 + 프로세스"라는 말이 더 익숙합니다.
먼저 이 인터뷰 질문을 데이터의 관점에서 살펴보면 다음과 같은 사실을 알 수 있습니다.
1 2차원 배열(예: PHP 언어)을 사용하여 설명할 수 있습니다. 양휘삼각형의 첫 번째 N행
[ [1], [1, 1], [1, 2, 1], [1, 3, 3, 1], ]
2. 데이터 행 사이에는 다음과 같은 규칙이 있습니다.
1) 각 행의 양쪽에 있는 숫자는 항상 1
2) 각 행의 중앙에 있는 숫자입니다. 는 이전 행의 교차점에 있는 두 숫자의 합입니다
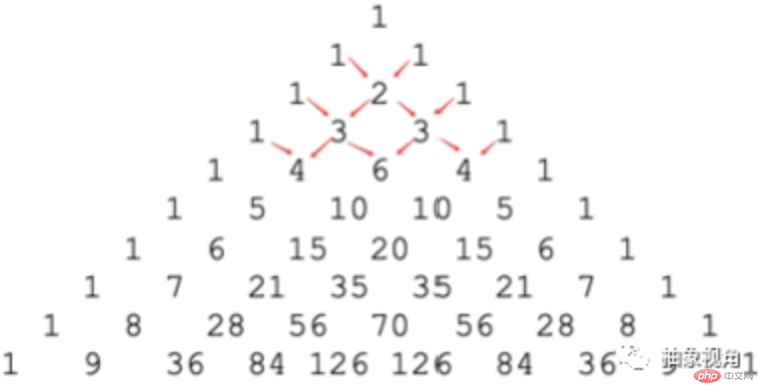
따라서 이 관계는 의사코드로 설명할 수 있습니다:
F(1) = [1]
F(N) = [
1,
F(N-1)[0] + F(N-1)[1],
F(N-1)[1] + F(N-1)[2],
...,
F(N-1)[N-2] + F(N-1)[N - 1],
1
]다음으로, 프로세스 관점에서 이 인터뷰 질문을 살펴보겠습니다. 우선, 프로세스는 두 단계로 나눌 수 있습니다: 1) 양휘 삼각형의 첫 번째 N 행의 데이터를 얻습니다. 2) 다이어그램에 표시된 정렬에 따라 인쇄합니다.
첫 번째 단계는 이전 데이터 분석을 기반으로 해당 방법 설계를 쉽게 그릴 수 있습니다.
function yanghui_datas($n); // 获取前N行杨辉三角数据 function yanghui_line_datas($prev_line_data); // 依据前一行数据获取下一行数据
두 번째 단계는 다이어그램 정렬에 따라 인쇄합니다. 순수 프린팅은 매우 간단하기 때문에 핵심은 '정렬'입니다.
정렬 문제를 해결하는 방법은 해당 위치를 비워 두는 것입니다. 하지만 어떻게 여백을 남겨둘 것인지가 명확하지 않은 것으로 나타났습니다. 그렇다면 더 생각해보면, 여백 속에서 논리가 불분명해지는 난제들은 무엇일까?
분석을 통해 처음 5줄만 출력하면 각 숫자가 6번째 줄을 출력하려면 10자리가 시작되는 것을 알 수 있습니다. 따라서 여기서 어려움을 야기하는 것은 숫자의 폭에 대한 불확실성입니다.
반대로 생각해보면 숫자의 폭이 정해져 있으면 이런 어려움은 없을 것 같아요. 따라서:
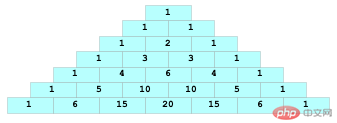
각 숫자를 동일한 너비의 그리드에 넣습니다. 이런 식으로 전체 문제가 명확해집니다.
格子宽度 = 最大数字宽度 + 1 行前留白 = (LINE_COUNT - LINE_NO) * 格子宽度 / 2 格子内部: (数字居中) 左留白 = (格子宽度 - 数字宽度) / 2 右留白 = 格子宽度 - 左留白 - 数字宽度
위의 분석 후에 코드가 거의 종이에 나타납니다.
// 获取前N行杨辉三角数据
function yanghui_datas($n_line) {
$datas = [];
$prev_line_datas = [];
while ($n_line -- > 0) {
$line_datas = yanghui_line_datas($prev_line_datas);
array_push($datas, $line_datas);
$prev_line_datas = $line_datas;
}
return $datas;
}
// 通过前一行数据获取下一行数据
function yanghui_line_datas($prev_line_datas) {
if (empty($prev_line_datas)) {
return [1];
}
$line_datas = [];
array_push($line_datas, 1); // 行首
for ($i = 1; $i < count($prev_line_datas); $i ++) {
array_push($line_datas, $prev_line_datas[$i - 1] + $prev_line_datas[$i]);
}
array_push($line_datas, 1); // 行尾
return $line_datas;
}
// 打印指定的杨辉三角数据
function yanghui_print($datas) {
$space = ' '; // 留白字符
$newline = '<br />'; // 换行符
$max_num = yanghui_max_num($datas); // 最大数字
$max_num_width = yanghui_num_width($max_num); // 最大宽度
$unit_width = $max_num_width + 1; // 格子宽度
$line_count = count($datas); // 行数
foreach ($datas as $idx => $line_datas) {
$line_no = $idx + 1; // 行号
$line_prefix_width = ($line_count - $line_no) * $unit_width / 2; // 行前留白数
echo str_repeat($space, $line_prefix_width);
foreach ($line_datas as $num) {
$num_width = yanghui_num_width($num); // 数字宽度
$left_width = intval(($unit_width - $num_width) / 2); // 格子内左留白宽度
$right_width = $unit_width - $left_width - $num_width; // 格子内右留白宽度
echo str_repeat($space, $left_width);
echo $num;
echo str_repeat($space, $right_width);
}
echo $newline;
}
}
// 获取最大数
function yanghui_max_num($datas) {
$max = 0;
foreach ($datas as $line_datas) {
foreach ($line_datas as $num) {
$max = max($max, $num);
}
}
return $max;
}
// 获取数字的宽度
function yanghui_num_width($num) {
return strlen(strval($num));
}결국 프로세스의 두 부분이 결합되어 원하는 결과를 얻습니다.
function yanghui_dump($n) {
$datas = yanghui_datas($n);
yanghui_print($datas);
}어떤 사람들은 양희의 삼각형에 있는 숫자가 좌표를 기준으로 직접 계산될 수 있다고 말합니다. 데이터에서 해당 부분을 바꾸면 됩니다.
우리가 문제에 직면할 때 경험 기반 사고와 능력 기반 사고의 두 가지 방식이 있습니다.
경험적 사고, 나만의 지식 기반 검색을 통해 양휘의 삼각형이 2층 사이클이어야 한다는 것을 발견하고 이를 실행하기 시작했는데, 한 단계를 실행한 후 다음 질문이 내 안에 있지 않다는 것을 발견했습니다. 지식 베이스를 보고 명상에 빠졌어요!
능력적 사고, 먼저 문제의 필수 구성요소를 분석하고, 문제를 분해하고, 복잡한 큰 문제를 여러 개의 단순한 작은 문제로 변환하고, 고치를 벗겨내고, 각각의 작은 문제에 대한 답을 자신의 지식 기반에서 검색하고, 마지막으로 문제를 해결하세요.
두 가지 사고 모드의 장점과 단점은 분명합니다. 경험 기반 사고는 특정하고 알려진 간단한 문제를 해결하는 데 적합하며, 능력 기반 사고는 불확실하고 알려지지 않은 복잡한 문제를 해결하는 데 적합합니다. 그리고 더 넓은 적응성을 가지고 있습니다.
프로그래밍은 논리와 추론에 중점을 두는 매우 창의적인 직업입니다.
프로그래밍을 시작하기 전에 먼저 특정 문제의 관점에서 대상 시스템을 분석한 다음 추상적인 관점에서 대상 시스템을 분석하여 더 높은 수준의 추론을 수행해야 합니다. 구체적인 것과 추상적인 것 사이에서 우리는 현실에 대한 합리적인 추상적인 설명을 찾기 위해 끊임없이 고민합니다.
이러한 분석과 추론의 과정은 사물의 본질을 찾는 과정입니다. 그러나 일상 업무에서 우리는 수많은 복잡한 요구 사항에 직면하고 있으며 디자인 수준에 대해 생각할 시간이 많지 않습니다. 현실은 우리를 수요 번역 기계로 만들었습니다.
대부분의 프로그래머는 실제로 이것을 꺼려하므로, 기꺼이 변화를 추구하고 그러한 변화의 달성을 촉진하려는 학생들에게 튜토리얼을 사용하고 싶습니다.
현재 회사에서 사용하고 있는 프레임워크를 2014년에 작성했는데 5년 넘게 안정적으로 운영되고 있으며 60만 라인 이상의 비즈니스 코드를 지원하지만 코드가 6,000라인에 불과합니다. 다음에는 프레임워크를 다시 작성한다는 관점에서 프레임워크 작성에 대한 사고, 분석, 설계, 구현의 전 과정을 종합적으로 재현하여 동영상 튜토리얼로 정리하여 청사진으로 활용하겠습니다. 모든 사람이 프로그래밍의 느낌을 찾는 데 도움이 될 수 있습니다. (자발적 결제, 무료 공유 및 배포)
전체 튜토리얼은 대략 12개의 강의로 구성되어 있으며, 각 강의는 독립적인 주제를 가지고 있으며, 각 강의는 1~3시간 동안 진행되며 공개 계정 기사가 함께 제공됩니다. 대규모 프레임워크는 외부 환경과의 상호 작용, 비즈니스 계층의 캡슐화 제약, ORM과 같은 보조 도구의 세 부분으로 나뉩니다.
텍스트의 표현력이 제한되어 있어 이 글은 경력 개발에 대한 구체적인 분석과 튜토리얼이 전달하고자 하는 가치, 그리고 그 가치를 전달하는 데 사용되는 방법을 다운로드하는 데만 사용됩니다. 심층 학습을 위한 비디오 튜토리얼.
[Ten Years of Sword, Understanding Abstract Thinking through Frameworks]는 프레임워크 개발의 사고, 분석, 설계, 구현의 전 과정을 재현하여 누구나 프로그래밍에 대한 영감을 얻을 수 있도록 도와주는 튜토리얼 시리즈입니다. 지불, 무료 배포 및 공유). 튜토리얼은 공개 계정 "Abstract Thinking"을 통해 공개됩니다.
오늘 공개되는 것은 첫 번째 강의 "녹음 튜토리얼의 의미"입니다. 관심이 있고 더 자세히 알고 싶으시면 QR 코드를 스캔하여 비디오 튜토리얼을 다운로드하십시오(주소: https://pan.baidu. com/wap/init?surl =IZ24Az5GFpQoQSD4WbfR8g 추출 비밀번호: rcga)
위 내용은 프로그래머, 앞으로 몇 년 동안 이 일을 할 수 있나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!