PHP 기반의 힙 정렬 원리 구현

Heap

Heap은 컴퓨터 과학에서 특별한 유형의 데이터 구조에 대한 총칭이며 일반적으로 트리로 볼 수 있는 배열 개체입니다.

힙 {k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1 ,2,3,4...n/2)

힙 정보:

• 힙에 있는 노드의 값은 항상 상위 노드의 값보다 크거나 작지 않습니다.
• 힙은 항상 트리 완전 이진 트리입니다(아래).
• 가장 큰 루트 노드가 있는 힙을 최대 힙 또는 대형 루트 힙이라고 하며, 가장 작은 루트 노드가 있는 힙을 최소 힙 또는 작은 루트 힙이라고 합니다.

완전 이진 트리

힙 정렬에 관해서는 완전 이진 트리를 언급해야 합니다. 이러한 기본 개념은 인터넷 어디에나 있습니다. 저는 가장 간단한 것을 골랐습니다. .

완전 이진 트리: 마지막 레벨을 제외하고 각 레벨의 노드 수가 최대값에 도달합니다. 마지막 레벨에서는 오른쪽에 있는 몇 개의 노드만 누락됩니다.

개인적으로는 다음 두 가지 특성 때문이라고 개인적으로 결론 내렸습니다.

• 마지막 레이어에만 빈 노드가 있을 수 있고 빈 노드는 오른쪽에 있습니다. 즉, 리프 노드는 가장 큰 두 레이어에만 나타날 수 있습니다( 저장 방법 규칙성)
• i>1인 경우 트리의 부모는 tree[i p 2]입니다(부모 및 자식 노드 값의 규칙성).

정렬이 매우 편리합니다.

힙 정렬

힙 정렬은 오름차순에는 큰 상단 힙을 사용하고 내림차순에는 작은 상단 힙을 사용합니다.

이 예에서는 작은 상위 힙을 내림차순으로 사용하여 분석합니다.

힙 정렬 단계는 다음과 같습니다.

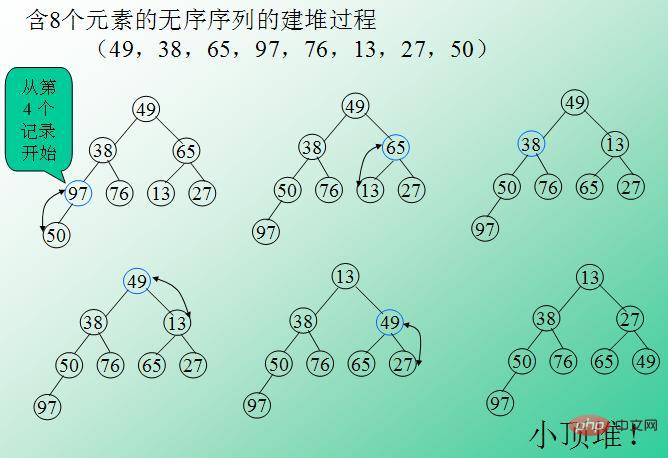
1. 데이터(49, 38, 65, 97, 76, 13, 27, 50)에서 $arr 배열을 만듭니다.

2. arr을 사용하여 작은 Top 힙을 만듭니다. (주요 단계는 코드 주석에서 설명합니다. 아래 그림은 배열을 사용하여 작은 Top 힙을 만드는 과정입니다.)

3. 힙의 루트(가장 작은 요소)를 교환합니다. ) 마지막 리프로 힙의 길이를 변경하고 1을 줄이고 두 번째 단계로 점프합니다.

4. 힙에 노드가 하나만 있고 정렬이 완료될 때까지 2-3단계를 반복합니다.

힙 정렬의 PHP 구현

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2; 
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);

//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);

for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);  
}

//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
  //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
  //从$index处对一个树进行循环比较,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左节点,将其下标存进最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }  
    }
  }
}

//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

다음은 정렬의 최종 결과입니다.

Heap은 전체 정렬에 사용되며 시간 복잡도는 O(nlogn)

그리고 퀵 정렬을 전체 정렬에 사용하면 평균 시간 복잡도도 O(nlogn)입니다

그러나 힙 정렬을 사용하여 TopK를 찾을 수 있는 경우 힙의 시간 복잡도는 K만 필요하므로 O(Klog2(n)입니다.

추천 튜토리얼: "PHP"

위 내용은 PHP 기반의 힙 정렬 원리 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!