Java에서 이진 트리의 깊이 우선 순회에 대한 자세한 설명-java지도 시간-php.cn

Java에서 이진 트리의 깊이 우선 순회에 대한 자세한 설명

지난 이틀 동안 이진 트리와 관련된 알고리즘 문제를 풀고 학습노트를 작성했습니다. (이진 트리를 어떻게 하는지도 모르시나요? 정말 능숙하지도 않고, 일상 업무에서 이진 트리와 관련된 알고리즘이나 데이터 구조를 작성할 필요도 없습니다. 제가 잘 못하기 때문에, 더 열심히 공부하기!)

Definition

아래 Wikipedia의 설명을 먼저 읽어보세요. 컴퓨터 과학에서 binary tree(영어: Binary tree)는 각 노드가 최대 두 개의 가지를 갖는 트리 구조입니다. 즉, 분기 차수가 2보다 큰 노드가 없습니다.) 일반적으로 가지를 "왼쪽 하위 트리" 또는 "오른쪽 하위 트리"라고 합니다. 이진 트리의 가지에는 왼쪽과 오른쪽 순서가 있으며 마음대로 되돌릴 수 없습니다.

이진 트리 자체가 정의한 특성으로 인해 로컬 반복성이 높기 때문에 이진 트리 깊이 우선 순회 시 일반적으로 이런 방식으로 구현된 코드는 매우 간단합니다. 아름답고 이해하기 쉽습니다.

깊이 우선 순회

일반적으로 이진 트리의 깊이 우선 순회에는 사전 주문, 중간 주문, 사후 주문이라는 가장 일반적인 세 가지 순서 순회가 있습니다.

선주문 순회 순서는 루트 노드 방문 -> 왼쪽 하위 트리 순회 -> 오른쪽 하위 트리 순회

중순 순회 순서는 왼쪽 하위 트리 순회 -> 루트 방문입니다. 노드-> 오른쪽 하위 트리 탐색

후위 순회 순서는 다음과 같습니다: 왼쪽 하위 트리 탐색-> 오른쪽 하위 트리 탐색-> 루트 노드 방문

여기서 왼쪽과 오른쪽은 전체 하위 트리입니다. 전체 트리를 순회해야 하므로 각 순회는 리프 노드까지 이 순서대로 수행됩니다.

예를 들어 다음과 같은 이진 트리가 있는 경우:

Java에서 이진 트리의 깊이 우선 순회에 대한 자세한 설명

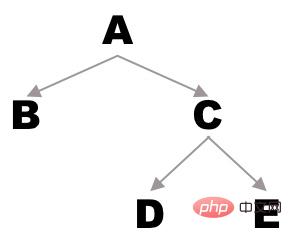
선순서 탐색으로 얻은 시퀀스는 A - B - C - D - E

중순 순회로 얻은 시퀀스는 B - A입니다. - D - C - E

후위 순회를 통해 얻은 시퀀스는 B - D - E - C - A

선순 순회를 아이디어로 활용해 보겠습니다. (적어도 인간 재귀를 수행하는 것은 매우 권장되지 않습니다. 내 뇌는 세 가지 수준을 처리할 수 없습니다...):

재귀의 첫 번째 수준:

루트 노드를 먼저 방문하여 루트 노드 A가 출력된 다음 왼쪽 하위 트리(L1)를 순회한 다음 오른쪽 하위 트리를 순회합니다. (R1);

재귀의 두 번째 수준:

L1의 경우 루트 노드를 먼저 방문하므로 이때 루트 노드 B를 출력한 다음 B의 왼쪽 및 오른쪽 하위 트리가 비어 있음을 확인하고 재귀를 종료합니다. ;

R1의 경우 먼저 루트 노드를 방문하므로 이때 루트 노드 C를 출력한 다음 왼쪽 하위 트리(L2)를 순회한 다음 오른쪽 하위 트리(R2)를 순회합니다.

재귀의 세 번째 수준:

L2의 경우 루트 노드를 먼저 방문하므로 이때 루트 노드 D가 출력되고 D가 발견됩니다. E의 왼쪽 및 오른쪽 하위 트리가 비어 있고 재귀가 종료됩니다.

R2의 경우 루트 노드; 가 먼저 방문되므로 이때 루트 노드 E가 출력되고 그 후 E의 왼쪽 및 오른쪽 하위 트리가 비어 있는 것으로 확인되고 재귀가 종료됩니다.

앞 중간 Pre-order, Middle-order, Post-order의 정의에 따르면 실제로 다음과 같은 특징을 찾는 것은 어렵지 않습니다. • Pre-order의 첫 번째 노드는 루트 노드여야 하며, 마지막 노드는 후위 중 하나는 루트 노드여야 합니다

• 각 정렬의 왼쪽 하위 트리와 오른쪽 하위 트리의 분포는 규칙적입니다

• 위의 두 규칙을 따르는 모든 하위 트리에 대해

이러한 특성은 또한 정의의 순서 표현.

Java에서 이진 트리의 깊이 우선 순회에 대한 자세한 설명

다양한 파생

다음은 이진 트리 순회에 대한 가장 기본적인 알고리즘 질문 중 일부입니다. • 이진 트리가 주어지면 사전/중간/사후 순서 순회 순서를 얻습니다.

• 선순서(Preorder)와 중위순(Inorder)은 후순(또는 전체 이진 트리)을 추론하는 데 사용됩니다.

• 선순서(또는 전체 이진 트리)의 파생은 후순 및 중순을 기반으로 합니다.

이진 트리 순회에서는 일반적으로 다음을 수행합니다. 재귀적으로 적용할 수 있는 템플릿이 있습니다:

public void recur(int level, int param) {
    
    // terminator
    if (level > MAX_LEVEL) {
        // process result
         return;   
    }
    
    // process current logic
    process(level, param);
    
    // drill down
    recur(level+1, newParam);
    
    // restore current status
}

로그인 후 복사

지난 이틀 동안 Geek Time에서 시청한 알고리즘 훈련 캠프에서 차오 형제(친차오)가 언급한 좀 더 실용적인 팁입니다(이 템플릿) 특히 초보자에게 유용합니다) 좋습니다) 위의 세 단계(해제해야 할 지역 변수가 있거나 추가 처리가 필요한 경우 네 번째 단계 수행)를 따르면 보다 질서정연한 방식으로 재귀 코드를 작성할 수 있습니다.

다음은 pre-order와 in-order를 기반으로 post-order를 도출하는 예입니다.

먼저 두 시퀀스를 초기화합니다.

int[] preSequence = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] inSequence = {2, 3, 1, 6, 7, 8, 5, 9, 4};

로그인 후 복사

위에서 언급한 여러 기능을 통해 우리는 이미 최소 반복 하위 문제를 찾을 수 있습니다. recursion

preorder의

첫 번째 노드 값

에 따라 중위에서 노드 값이 있는 인덱스 i를 일치시켜 왼쪽 및 오른쪽 하위 트리에 각각 해당하는 인덱스 i의 앞부분과 뒷부분을 얻을 수 있습니다. , 두 개의 왼쪽 및 오른쪽 하위 트리를 각각 순회한 다음 현재 선주문의 첫 번째 노드 값인 루트 노드를 출력합니다.

하향식 프로그래밍 방법에 따라 먼저 다음과 같은 초기 재귀 호출을 작성할 수 있습니다.

List<Integer> result = new ArrayList<>();
preAndInToPost(0, 0, preSequence.length, preSequence, inSequence, result);

로그인 후 복사

첫 번째 매개변수는 선주문 시퀀스의 첫 번째 요소 인덱스를 나타냅니다.

두 번째 매개변수는 중위 시퀀스를 나타냅니다.

세 번째 매개변수는 시퀀스 길이를 나타냅니다.

第四个参数表示前序序列；

第五个参数表示后序序列；

第六个参数用于保存结果；

先来考虑终止条件是什么，也就是什么时候结束递归，当我们的根结点为空的时候终止，对应这里就是序列长度为零的时候。

if (length == 0) {
    return;
}

로그인 후 복사

接着考虑处理逻辑，也就是找到索引 i：

int i = 0;
while (inSequence[inIndex + i] != preSequence[preIndex]) {
    i++;
}

로그인 후 복사

然后开始向下递归：

preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
result.add(preSequence[preIndex]);

로그인 후 복사

因为推导的是后序序列，所以顺序如上，添加根结点的操作是在最后的。前三个参数如何得出来的呢，我们走一下第一次遍历就可以得出来。

前序序列的第一个结点 1 在中序序列中的索引为 2，此时

左子树的中序系列起始索引为总序列的第 1 个索引，长度为 2；

左子树的前序序列起始索引为总序列的第 2 个索引，长度为 2；

右子树的中序系列起始索引为总序列的第 3 个索引，长度为 length - 3；

右子树的前序序列起始索引为总序列的第 3 个索引，长度为 length - 3；

完整代码如下：

/**
 * 根据前序和中序推导后序
 *
 * @param preIndex    前序索引
 * @param inIndex     中序索引
 * @param length      序列长度
 * @param preSequence 前序序列
 * @param inSequence  中序序列
 * @param result      结果序列
 */
private void preAndInToPost(int preIndex, int inIndex, int length, int[] preSequence, int[] inSequence, List<Integer> result) {
    if (length == 0) {
        return;
    }

    int i = 0;
    while (inSequence[inIndex + i] != preSequence[preIndex]) {
        i++;
    }

    preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
    preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
    result.add(preSequence[preIndex]);
}

로그인 후 복사