PHP의 피보나치 수열을 위한 N 알고리즘

머리말

얼마 전 피보나치 수의 계산을 최적화하는 기존의 재귀적 방법을 접했지만 제때에 좋은 방법이 생각나지 않아 나중에 관련 정보를 찾아보며 많이 정리한 계산 솔루션이 있어서 모두와 공유하고 소통하며 배웁니다.

추천: "PHP 비디오 튜토리얼"

피보나치 수열이란 무엇입니까

황금분할 수열이라고도 알려진 피보나치 수열은 수학자 레오나르도 피보나치 레오나르도 피보나치가 토끼 번식의 예를 들어 소개했기 때문에, 그래서 "토끼 수열"이라고도 하는데, 1, 1, 2, 3, 5, 8, 13, 21, 34,… … 수학적으로 피보나치 수열은 다음과 같이 재귀적으로 정의됩니다. F (1)=1, F(2)=1, F(n)=F(n - 1)+F(n - 2) (n ≥ 3, n ∈ N*).

이제 피보나치 수를 알았으니 다양한 방법을 사용하여 N번째 피보나치 수를 계산하고 구해 보겠습니다. 斐波那契数，那么下面我们就用多种不同的方法来计算获取第N位斐波那契数。

普通递归

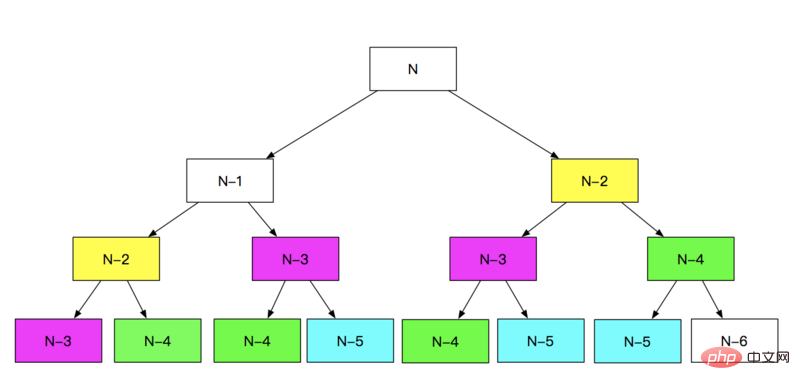
这种方法是最常规的，直接根据定义F(n)=F(n - 1)+F(n - 2)递归计算即可，但是性能是最低的。

/**
 * 普通递归
 * @param int $n
 * @return int
 */function fib($n = 1){    // 低位处理
    if ($n < 3) {        return 1;
    }    // 递归计算前两位
    return fib($n - 1) + fib($n - 2);
}

递归优化

从上面的递归方法可以看到，进行了很多的重复计算，性能极差，如果N越大，计算的次数太可怕了，那么，既然因为重复计算影响了性能，那么优化就从减少重复计算入手，即把之前计算的存储起来，这样就避免了过多的重复计算，优化了递归算法。

/**
 * 递归优化
 * @param int $n
 * @param int $a
 * @param int $b
 * @return int
 */function fib_2($n = 1, $a = 1, $b = 1){    if ($n > 2) {        // 存储前一位，优化递归计算
        return fib_2($n - 1, $a + $b, $a);
    }    return $a;
}

记忆化自底向上

自底向上通过迭代计算斐波那契数的子问题并存储已计算的值，通过已计算的值进行计算。使用for循环，减少递归带来的重复计算问题。

/**
 * 记忆化自底向上
 * @param int $n
 * @return int
 */function fib_3($n = 1){
    $list = [];    for ($i = 0; $i <= $n; $i++) {        // 从低到高位数，依次存入数组中
        if ($i < 2) {
            $list[] = $i;
        } else {
            $list[] = $list[$i - 1] + $list[$i - 2];
        }
    }    // 返回最后一个数，即第N个数
    return $list[$n];
}

自底向上进行迭代

最低位初始化赋值，使用for从低位到高位迭代计算，从而得到第N个数。

/**
 * 自底向上进行迭代
 * @param int $n
 * @return int
 */function fib_4($n = 1){    // 低位处理
    if ($n <= 0) {        return 0;
    }    if ($n < 3) {        return 1;
    }
    $a = 0;
    $b = 1;    // 循环计算
    for ($i = 2; $i < $n; $i++) {
        $b = $a + $b;
        $a = $b - $a;
    }    return $b;
}

公式法

通过了解斐波那契序列和黄金分割比之间的关系，使用黄金分割率计算第N

일반 재귀

이 방법은 F(n)=F(n - 1)+F(n - 2) 정의에 따라 재귀적으로 계산할 수 있습니다. 그러나 성능은 미미합니다.

/**
 * 公式法
 * @param int $n
 * @return int
 */function fib_5($n = 1){    // 黄金分割比
    $radio = (1 + sqrt(5)) / 2;    // 斐波那契序列和黄金分割比之间的关系计算
    $num = intval(round(pow($radio, $n) / sqrt(5)));    return $num;
}

재귀적 최적화

위의 재귀적 방법에서 볼 수 있듯이 반복적인 계산이 많이 수행되고 성능이 극도로 나빠집니다. N이 커지면 계산 횟수가 너무 끔찍해지기 때문입니다. 반복 계산이 성능에 영향을 미치면 반복 계산을 줄이는 것, 즉 이전 계산을 저장하여 너무 많은 반복 계산을 피하고 재귀 알고리즘을 최적화하는 것부터 최적화가 시작됩니다.

/**
 * 无敌欠揍法
 * @param int $n
 * @return int
 */function fib_6($n = 1){    // 列举了30个数
    $list = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269];    return $list[$n];
}

Memory Bottom-up

Bottom-up은 피보나치 수열의 하위 문제를 반복적으로 계산하여 계산된 값을 저장하고, 계산된 값을 기반으로 계산을 수행합니다. 재귀로 인해 발생하는 이중 계산 문제를 줄이려면 for 루프를 사용하세요.

rrreee

아래에서 위로 반복

🎜🎜최하위 비트 할당을 초기화하고 for를 사용하여 낮은 비트에서 높은 비트까지 반복 계산하여 N번째 숫자를 얻습니다. 🎜rrreee🎜🎜공식 방법🎜🎜🎜피보나치 수열과 황금비의 관계를 이해함으로써 황금비를 이용하여 N번째 피보나치 수를 계산합니다. 🎜rrreee🎜🎜무적의 방법🎜🎜🎜이 방법에 대해서는 많이 말하지 않겠습니다. 모두가 알고 있지만 쉽게 시도하지 마세요...🎜🎜🎜🎜🎜🎜rrreee🎜🎜드디어🎜🎜🎜그래요, 나 여러 가지 해결 방법을 대략적으로 작성해 놓았습니다. 잘못된 부분이 있으면 지적해 주시면 수정하겠습니다. 다른 계산 방법이 있으면 공유해 함께 소통하고 배워 보세요. 🎜🎜🎜🎜

위 내용은 PHP의 피보나치 수열을 위한 N 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!