컴퓨터의 음수가 2의 보수로 저장되는 이유는 무엇입니까?
컴퓨터에서 음수에 2의 보수 저장 장치를 사용하면 기본 컴퓨터 산술 회로가 단순화되므로 덧셈과 뺄셈은 덧셈 회로로만 구현하면 되고 뺄셈 대신 덧셈이 사용됩니다. 보수는 음수의 가장 작은 양수 합동 나머지이므로 음수를 더하는 것과 양수를 빼는 것은 모두 보수를 더하는 것으로 표현될 수 있습니다.

이 튜토리얼의 운영 환경: Windows 7 시스템, Dell G3 컴퓨터.
1. 소개
컴퓨터에 정수가 어떻게 저장되는지 아시나요? 부호 비트에 값 비트를 더한 것입니까? 값 비트가 일반 바이너리 형식으로 저장되어 있습니까?
마지막 두 질문에 '예'라고 대답하면 3비트 바이너리로 저장되고 부호 비트 0이 양수를 나타내고 1이 음수를 나타내면 1이 001, -1로 저장된다는 의미입니다. 101로 저장됩니다. 불행하게도 컴퓨터는 현재 자연스러운 형식 대신 2의 보수 형식으로 정수를 저장합니다. 2의 보수도 부호 비트와 값 비트로 표시되지만 표현 규칙은 다릅니다. 1은 001로 저장되고, -1은 111로 저장됩니다. 001,-1会存储成101。可惜事实不是这样,计算机中是用补码的形式而不是刚刚那种看上去很自然的形式存储整数,补码虽然也是用符号位加值位来表示,但表示的规则不太一样:1会存成001,-1会存成111。
如果三个问题你都回答对了,你知道计算机中整数以补码的形式存储,但你知道为什么要用这种形式吗?以及「正数的补码等于原码;负数的补码等于反码加1,而反码等于原码符号位不变,其余各位取反」这样的补码到底意味着什么?(假设你不知道,请接着往下看吧 XD)
先看使用补码的目的,然后忘掉上面那个补码定义,跟我从这个目的开始,一步步探索补码的本质。
目的:为了简化计算机基本运算电路,使加减法都只需要通过加法电路实现,也就是让减去一个正数或加上一个负数这样的运算可以用加上一个正数来代替。于是改变负数存储的形式,存储成一种可以直接当成正数来相加的形式,这种形式就是补码。(正数不用变,所以接下来的讨论中一般略去正数)
2.补码是怎么把减法变成加法的?
2.1.用时钟理解减法变加法
这是一个身边的例子,当你校对时钟的时候,假设发现钟是6点,但实际上现在才2点,也就是它走快了4个小时,你可以有两种方法进行校正,一种是逆时针拨回4个小时到2点,另一种是顺时针拨6个小时到12点然后再拨2小时,也就是顺时针拨8个小时到2点。所以对于时钟的表盘来说,设-N表示逆时针拨N个小时,N表示顺时针拨动N个小时,那么-4 = +8,同样还会有 -1 = +11、-5 = +7,甚至也可以 -4 = +8 = +20 = +32 = -16...
这里边隐藏了什么规律?其实在数学中,-4、+8、+20、+32、-16可以归为符合某个条件的同一类数字 —— 对于模12同余。
中文维基上对于模和同余的定义是:两个整数a、b,若它们除以正整数m所得的余数相等,则称a、b对于模m同余。
而在一个可溢出计数系统中,把计数系统容量作为模,那么所有对此模同余的数在此计数系统中都会有同样的表示,而且运算等价。
比如上面例子中的时钟表盘就是一个可溢出计数系统,模为12,所以-4、+8、+20、+32、-16这些对模12同余的数在时钟表盘上的表示是一样的,而且对时针做这些操作的结果也是一样的,都会拨到同样的位置。
一个n位二进制构成的计数系统,因为会舍弃溢出的高位,所以也是一个可溢出的计数系统,它的模为(2^n) 。(从0数到(2^n -1),再多就溢出)
由此可以推理,在一个3位二进制构成的模为8的计数系统中,-2,-10,6,14
세 가지 질문을 모두 올바르게 답하셨다면 컴퓨터에서 정수가 2의 보수 형식으로 저장된다는 사실을 아실 텐데, 이 형식이 왜 사용되는지 아시나요? 그리고
"양수의 보수는 원래 코드와 같고, 음수의 보수는 보수에 1을 더한 것과 같고, 보수는 변경되지 않은 원본 코드의 부호 비트와 같고, 나머지 비트는 거꾸로."이러한 보완은 무엇을 의미하나요? (모르는 분들은 XD를 읽어주세요) 먼저 보완코드를 사용하는 목적을 살펴보고, 위의 보완코드 정의는 잊어버리고 이 목적부터 따라오세요. 그리고 코드의 본질을 단계별로 탐구합니다.
목적: 기본적인 컴퓨터 연산 회로를 단순화하기 위해 덧셈과 뺄셈은 덧셈 회로를 통해서만 구현하면 됩니다. 즉, 양수 뺄셈 또는 음수 덧셈을 수행할 수 있습니다.
2. 보수 코드는 어떻게 뺄셈을 덧셈으로 바꾸나요?
2.1 뺄셈과 덧셈을 이해하려면 2시, 즉 4시간 더 빨리 가는 것을 두 가지 방법으로 수정할 수 있습니다. 하나는 시계 반대 방향으로 2시로 돌리는 것입니다. 시계, 다른 하나는 시계 방향으로 6시간을 돌려 12시 방향으로 돌린 다음 다시 2시간을 다이얼하는 것입니다. 즉, 시계 방향으로 8시간을 돌려 2시 방향으로 돌리는 것입니다. 따라서 시계 다이얼의 경우-N이 N시간을 시계 반대 방향으로 돌리는 것을 의미하고N이 N시간을 시계 방향으로 돌리는 것을 의미한다면-4 = +8입니다. ,-1 = +11,-5 = +7, 심지어-4 = +8 = + 20 = +32 = -16도 있습니다....여기에는 어떤 규칙이 숨겨져 있나요? 실제로 수학에서
합동 모듈로 12🎜에 대해 특정 조건을 충족하는 동일한 유형의 숫자로 분류될 수 있습니다. 🎜🎜-4, +8, +20, +32, -16은중국 위키에서 모듈러스와 합동의 정의는 다음과 같습니다. 두 개의 정수 a와 b, 이를 양의 정수 m으로 나누어 얻은 나머지가 같으면 a와 b는 다음과 같습니다. 모듈로 m을 유지하세요. 🎜🎜
오버플로 가능한 계산 시스템에서 계산 시스템의 용량을 모듈로로 취하면 이 모듈러스와 일치하는 모든 숫자는 이 계산 시스템에서 동일한 표현을 갖게 되며 작업은 동일합니다.
예를 들어, 위 예의 시계 다이얼은 모듈로 12인 오버플로 계산 시스템이므로-4, +8, +20, +32, -16은 모듈로 12와 일치합니다. 시계 다이얼의 숫자 표시는 동일하며 시침의 이러한 작동 결과도 동일하므로 모두 동일한 위치에 설정됩니다. 🎜n비트 바이너리로 구성된 카운팅 시스템입니다. 오버플로된 상위 비트는 버려지기 때문에 이 역시 오버플로 가능한 카운팅 시스템이며 모듈러스는 (2^n)입니다. (0부터 (2^n -1)까지 계산하면 더 이상 오버플로됩니다.)
3비트 바이너리 모듈로 8,-2, -10, 6으로 구성된 계산 시스템에서 추론할 수 있습니다. , 14는 동일한 이진수로 나타낼 수 있습니다. 10을 빼고 동시에 14를 더하면 같은 결과를 얻을 수 있습니다. 🎜🎜🎜🎜2.2. 보수 코드로 이어짐🎜🎜🎜🎜그래서 보수 코드가 음수의 양수 합동인 한, 이 양수 합동 보수 코드를 추가하는 것은 다음과 같은 효과를 얻을 수 있습니다. 또 다른 음수를 추가하세요🎜. 음수에 대해서는 조건을 만족하는 양의 합동이 무수히 존재하며, 불필요한 연산을 줄이기 위해 그 중에서 가장 작은 양수를 보수로 지정할 수 있다. 🎜🎜아마도 원본 코드를 통해 보완 코드를 찾는 것이 보완적인 모듈로 연산이기 때문에 보완 코드라고 부릅니다. 🎜🎜🎜여기의 보완 코드는 모두 제가 특별히 표시한 것입니다. 왜냐하면 이것은 컴퓨터에 저장된 실제 보완 형식이 아니기 때문입니다. 보완 번호라고 불러야 하지만, 매우 가깝습니다🎜.
3. 보완 코드 완성하기
3.1 이 보완 코드 표현에는 여전히 몇 가지 문제가 있습니다
보완 코드로 변환하면 숫자를 빼는 것이 숫자를 더하는 것이 됩니다. , 그러나 그러나 명백한 문제가 있습니다. 즉, 숫자 자체의 기호가 손실된다는 것입니다.
예를 들어 3자리 이진수는 일반적으로 0~7을 나타냅니다. 보수 방법을 사용하면 -8~-1의 연산을 대체할 수 있지만 - 8~-1, 양수인지 음수인지 알 수 없기 때문입니다. 0~7,使用补码法它能代替-8~-1的运算,但它不能真正表示-8~-1,因为你不知道它到底是正数还是负数。
我们把负数转换成了一种在运算中更让计算机喜欢的形式,但它却丢失了自己本身作为数的信息。
怎么解决这个问题,可能有人很快就拍脑袋:那就加一位来表示正负得了。但这样的话运算时怎么办,从第二位开始算么?那进位去位的时候是不是也需要特别注意一下不要影响到符号位?你会发现这个问题并不是那么简单。
3.2.怎么完善 补码
不知道大牛是怎么想到的,问题解决得非常完美:
- 在保持补码特性的前提下 (也就是减一个数还是照样变成加一个数)
- 增加正负的表示 (能真正表示
-8~-1음수를 계산 시 컴퓨터에 더 적합한 형식으로 변환했지만 숫자 자체에 대한 정보는 손실되었습니다. - 3.2. 보완 코드 개선 방법
이 문제를 해결하는 방법 어떤 사람들은 빨리 머리를 때릴 수 있습니다. 그런 다음 숫자 하나를 추가하여 양수 또는 음수를 나타냅니다. 그런데 이 경우 계산할 때 어떻게 해야 합니까? 두 번째 자리부터 계산을 시작해야 합니까? 비트를 수행할 때 부호 비트에 영향을 주지 않도록 특별히 주의해야 합니까? 문제가 그렇게 간단하지 않다는 것을 알게 될 것입니다.
다니엘이 어떻게 생각해냈는지는 모르겠지만 문제는 완벽하게 해결되었습니다:
-8을 표현할 수 있음) ~-1, 부호 비트가 0인지 1인지만 보세요) 그리고 해결책은 정말 멍청하고 놀랍도록 간단합니다. 이전에 생각했던 것:
양수와 음수를 나타내려면 숫자 하나를 추가하세요.
구체적인 방법은입니다. 왼쪽의 상위 비트에 부호 비트를 추가합니다. 이 부호 비트는 앞서 추론한 의사 보완 코드와 함께 정말 완벽한
보보 코드- 를 형성합니다.
- 얻은 효과: 부호 비트를 읽으면 숫자의 부호를 알 수 있습니다. 동시에 부호 비트는 덧셈 연산의 값 비트처럼 연산에 참여하고 전달합니다.
- 4. 마지막으로
- summarize
위 내용은 컴퓨터의 음수가 2의 보수로 저장되는 이유는 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7552
7552
 15
15
 1382
1382
 52
52
 83
83
 11
11
 59
59
 19
19
 22
22
 95
95
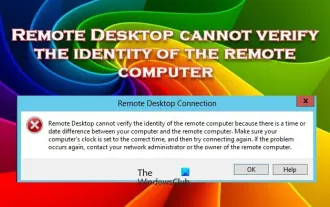 원격 데스크톱은 원격 컴퓨터의 ID를 인증할 수 없습니다.
Feb 29, 2024 pm 12:30 PM
원격 데스크톱은 원격 컴퓨터의 ID를 인증할 수 없습니다.
Feb 29, 2024 pm 12:30 PM
Windows 원격 데스크톱 서비스를 사용하면 사용자가 원격으로 컴퓨터에 액세스할 수 있으므로 원격으로 작업해야 하는 사람들에게 매우 편리합니다. 그러나 사용자가 원격 컴퓨터에 연결할 수 없거나 원격 데스크톱이 컴퓨터의 ID를 인증할 수 없는 경우 문제가 발생할 수 있습니다. 이는 네트워크 연결 문제 또는 인증서 확인 실패로 인해 발생할 수 있습니다. 이 경우 사용자는 네트워크 연결을 확인하고 원격 컴퓨터가 온라인인지 확인한 후 다시 연결을 시도해야 할 수 있습니다. 또한 원격 컴퓨터의 인증 옵션이 올바르게 구성되었는지 확인하는 것이 문제 해결의 핵심입니다. Windows 원격 데스크톱 서비스와 관련된 이러한 문제는 일반적으로 설정을 주의 깊게 확인하고 조정하여 해결할 수 있습니다. 원격 데스크톱은 시간 또는 날짜 차이로 인해 원격 컴퓨터의 ID를 확인할 수 없습니다. 계산을 확실히 해주세요
 2024년 CSRankings 전국 컴퓨터 과학 순위 발표! CMU가 목록을 장악하고 MIT가 상위 5위에서 벗어났습니다.
Mar 25, 2024 pm 06:01 PM
2024년 CSRankings 전국 컴퓨터 과학 순위 발표! CMU가 목록을 장악하고 MIT가 상위 5위에서 벗어났습니다.
Mar 25, 2024 pm 06:01 PM
2024CSRankings 전국 컴퓨터 공학 전공 순위가 방금 발표되었습니다! 올해 미국 최고의 CS 대학 순위에서는 카네기멜론대학교(CMU)가 CS 분야 전국 최고에 올랐고, 일리노이대학교 어바나-샴페인 캠퍼스(UIUC)가 1위를 차지했다. 6년 연속 2위를 기록했다. 조지아공대(Georgia Tech)가 3위를 차지했습니다. 이어 스탠퍼드대, 캘리포니아대 샌디에이고대, 미시간대, 워싱턴대가 공동 4위를 차지했다. MIT의 순위가 하락해 상위 5위권 밖으로 떨어졌다는 점은 주목할 만하다. CSRankings는 매사추세츠 대학교 Amherst 컴퓨터 및 정보 과학부의 Emery Berger 교수가 시작한 컴퓨터 과학 분야의 글로벌 대학 순위 프로젝트입니다. 순위는 객관적인 기준에 따라 결정됩니다.
 컴퓨터에서 e는 무엇입니까?
Aug 31, 2023 am 09:36 AM
컴퓨터에서 e는 무엇입니까?
Aug 31, 2023 am 09:36 AM
컴퓨터의 "e"는 과학 표기법에서 지수 구분 기호로 사용되며, 이는 "10의 거듭제곱"을 의미합니다. 과학 표기법에서 숫자는 일반적으로 M ×로 표시됩니다. 10^E, 여기서 M은 1에서 10 사이의 숫자이고 E는 지수를 나타냅니다.
 수정: Microsoft Teams 오류 코드 80090016 컴퓨터의 신뢰할 수 있는 플랫폼 모듈에 오류가 발생했습니다.
Apr 19, 2023 pm 09:28 PM
수정: Microsoft Teams 오류 코드 80090016 컴퓨터의 신뢰할 수 있는 플랫폼 모듈에 오류가 발생했습니다.
Apr 19, 2023 pm 09:28 PM
<p>MSTeams는 팀원 및 동료와 소통하고, 채팅하고, 통화할 수 있는 신뢰할 수 있는 플랫폼입니다. MSTeams의 오류 코드 80090016과 <strong>컴퓨터의 신뢰할 수 있는 플랫폼 모듈이 실패했습니다</strong>라는 메시지로 인해 로그인이 어려울 수 있습니다. 오류 코드가 해결될 때까지 앱에서 로그인을 허용하지 않습니다. MS Teams 또는 기타 Microsoft 응용 프로그램을 열 때 이러한 메시지가 나타나면 이 문서에서 문제 해결 방법을 안내할 수 있습니다. </p><h2&
 컴퓨터 CU는 무슨 뜻인가요?
Aug 15, 2023 am 09:58 AM
컴퓨터 CU는 무슨 뜻인가요?
Aug 15, 2023 am 09:58 AM
컴퓨터에서 cu의 의미는 상황에 따라 다릅니다. 1. 컴퓨터 중앙 프로세서의 제어 장치 CU는 전체 컴퓨팅 프로세스를 조정하고 제어하는 구성 요소입니다. 2. 그래픽 프로세서 또는 기타 장치의 컴퓨팅 장치 가속 프로세서인 CU는 병렬 컴퓨팅 작업을 처리하는 기본 단위입니다.
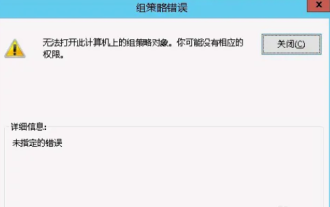 이 컴퓨터에서 그룹 정책 개체를 열 수 없습니다.
Feb 07, 2024 pm 02:00 PM
이 컴퓨터에서 그룹 정책 개체를 열 수 없습니다.
Feb 07, 2024 pm 02:00 PM
컴퓨터를 사용할 때 운영체제가 오작동하는 경우가 가끔 있습니다. 오늘 제가 겪은 문제는 gpedit.msc에 액세스할 때 올바른 권한이 부족할 수 있기 때문에 그룹 정책 개체를 열 수 없다는 메시지가 시스템에 표시된다는 것입니다. 이 컴퓨터의 그룹 정책 개체를 열 수 없습니다. 해결 방법: 1. gpedit.msc에 액세스할 때 시스템은 권한 부족으로 인해 이 컴퓨터의 그룹 정책 개체를 열 수 없다는 메시지를 표시합니다. 세부 정보: 시스템이 지정된 경로를 찾을 수 없습니다. 2. 사용자가 닫기 버튼을 클릭하면 다음과 같은 오류 창이 나타납니다. 3. 로그 기록을 즉시 확인하고 기록된 정보를 결합하여 C:\Windows\System32\GroupPolicy\Machine\registry.pol 파일에 문제가 있는지 확인합니다.
 보완 코드 란 무엇입니까?
Aug 09, 2023 pm 05:20 PM
보완 코드 란 무엇입니까?
Aug 09, 2023 pm 05:20 PM
1의 보수는 컴퓨터에서 이진수 연산에 일반적으로 사용되는 숫자 표현입니다. 보수 코드는 음수의 덧셈과 뺄셈 연산을 단순화하고 더 넓은 범위의 정수를 나타낼 수 있습니다. 보수 코드의 사용은 컴퓨터 과학에서 중요한 역할을 하며 컴퓨터에서 정수의 연산과 표현을 이해하는 데 매우 중요합니다.
 Steam이 원격 컴퓨터에 연결할 수 없으면 어떻게 해야 하나요?
Mar 01, 2023 pm 02:20 PM
Steam이 원격 컴퓨터에 연결할 수 없으면 어떻게 해야 하나요?
Mar 01, 2023 pm 02:20 PM
Steam이 원격 컴퓨터에 연결할 수 없는 문제에 대한 해결 방법: 1. 게임 플랫폼에서 왼쪽 상단에 있는 "steam" 옵션을 클릭합니다. 2. 메뉴를 열고 "설정" 옵션을 선택합니다. 4. "원격 재생" 기능 활성화를 선택하고 "확인" 버튼을 클릭하세요.



