이 전설에는 다양한 변형이 있으며 누구인지 알 수 없지만 남겨진 수학적 문제는 매우 고전적입니다.
그가 남긴 수학적 지식: 금 조각 수와 이동 단계 수의 관계는 2^n - 1입니다.
금 1개의 2승 - 1제곱의 이동 횟수2^n - 1。
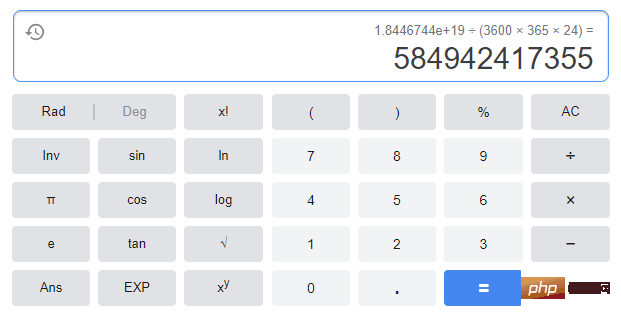
若传说属实，僧侣们需要 2^64 - 1 步才能完成这个任务；假设他们每秒移动一个金片，就需要 5849 亿年才能完成。整个宇宙现在也不过 137 亿年，所以宇宙毁灭还早…（闲的无聊，我还真计算了一下，如下图）
基本规则
汉诺塔算法有2个基本条件，假设移动的是盘子。
1.每次只能移动一个盘子。
2.小盘子必须要在大盘子的上面。
假设本次游戏有3根柱子，分别是 A， B， C。其中一根上已经有排序好的盘子N个，最大的在最下面，依次向上盘子越来越小，另外2根空柱子。
PHP가 흥미로운 하노이 타워 알고리즘을 구현하는 방법을 분석합니다.如下图：
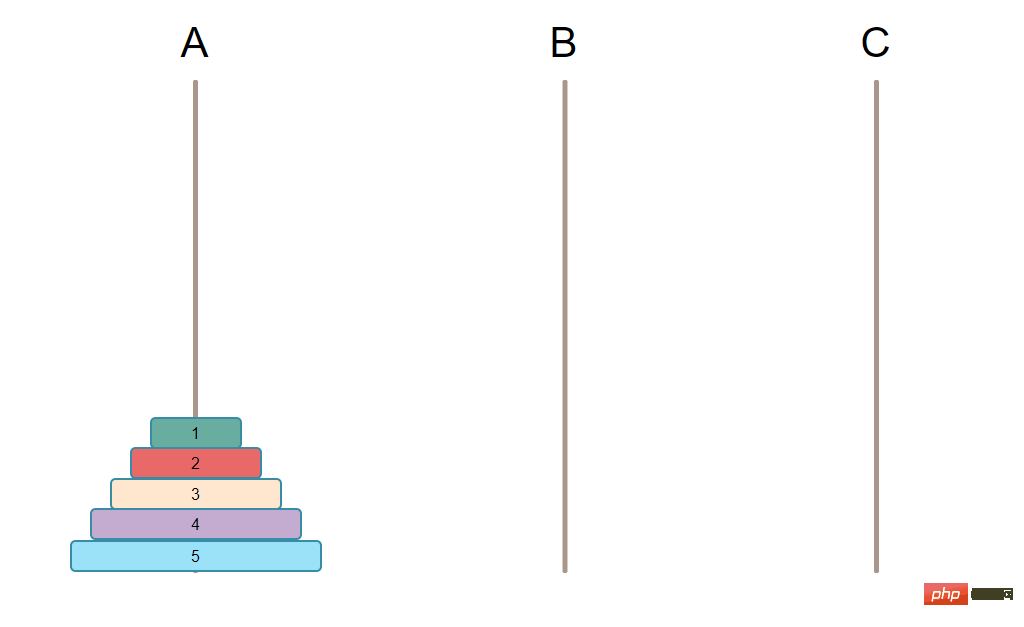
需要实现的最终目标是把柱子上所有的盘子都移动到另外一根柱子上。【推荐学习：PHP视频教程】
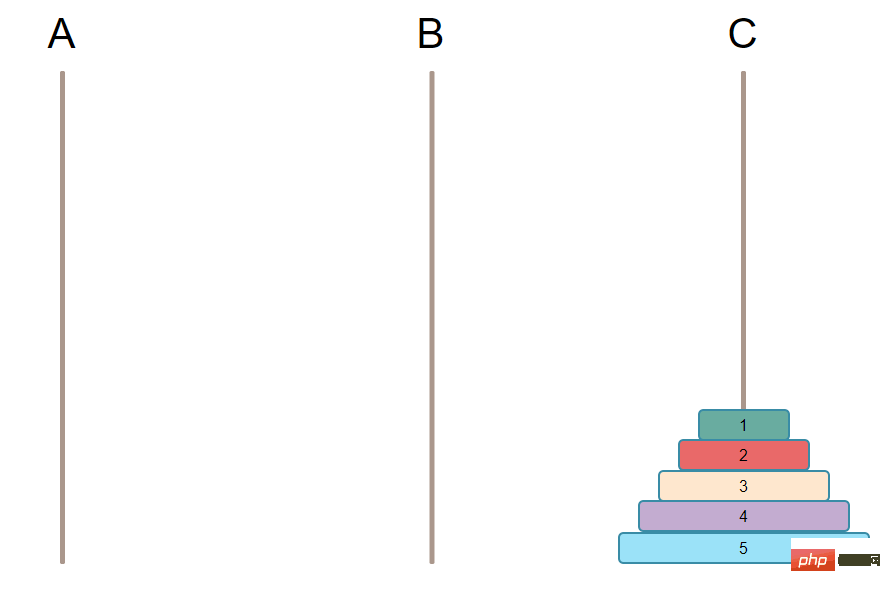
实现的大概思路：
N-1 个盘子都搬移到B柱子上，只有这样第N个盘子（也就是最大的盘子）才能移动到C柱子上。N-1 个盘子移动到B柱子上，因为要满足条件大的在下，小的在上，所以这 N-1
…
금 조각의 이동 횟수는 2의 n승 빼기 1입니다.
전설이 사실이라면 승려에게는2^64 - 1가 필요합니다. > 이 작업을 완료하는 단계는 각각 초당 하나의 금 조각을 이동하는 데 5,849억년이 걸린다고 가정합니다. 우주 전체의 나이는 고작 137억살이라 우주가 멸망하기엔 아직 이르다... (심심해서 실제로 계산을 해보니 아래와 같다)
기본 규칙
하노이 탑 알고리즘에는 2가지 기본 조건이 있습니다. 판이 옮겨졌다는 것입니다. 1. 한 번에 하나의 접시만 이동할 수 있습니다.
2. 작은 접시는 큰 접시 위에 놓아야 합니다.
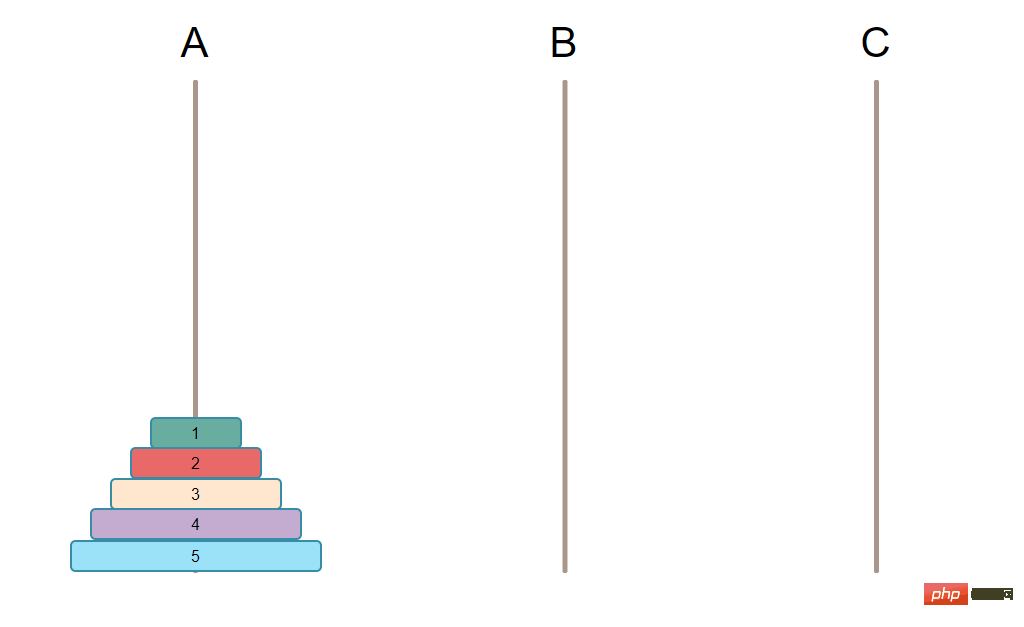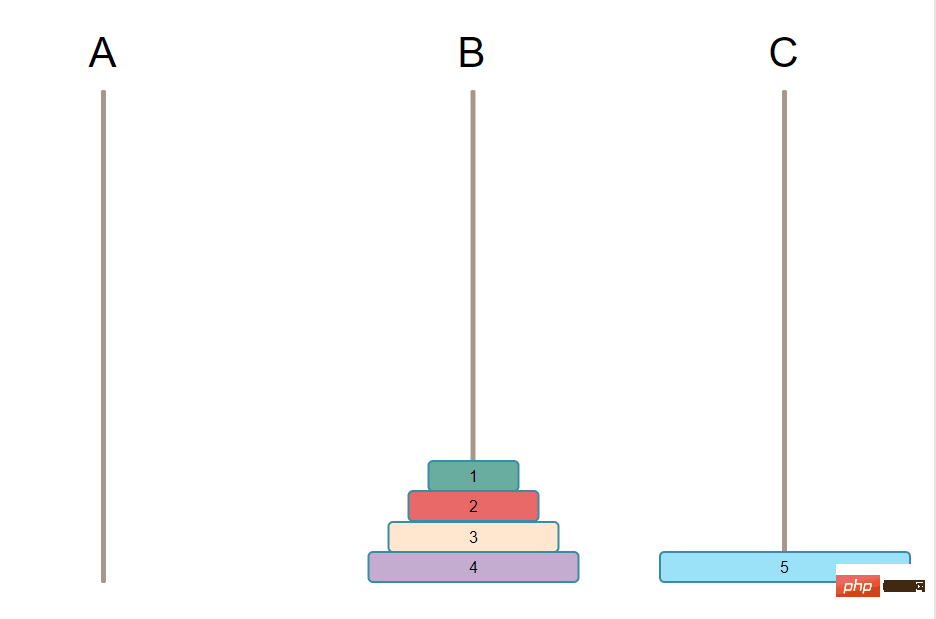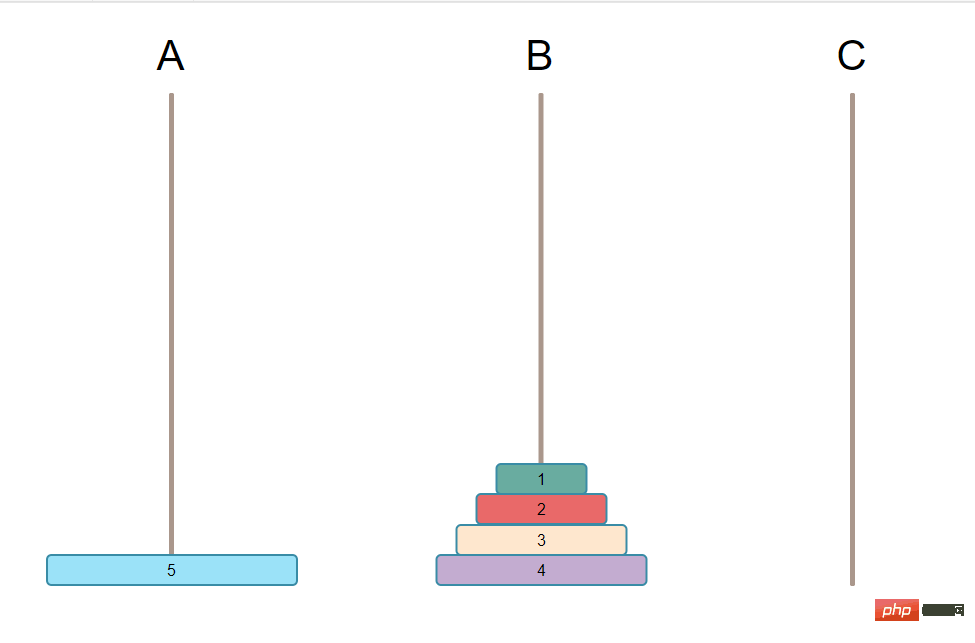
🎜🎜 달성해야 할 최종 목표는 기둥에 있는 모든 판을 다른 기둥으로 옮기는 것입니다. [추천 학습: PHP 동영상 튜토리얼]🎜🎜🎜🎜구현 아이디어에 대해: 🎜N-1 플레이트를 모두 B 기둥으로 이동해야 합니다. 이렇게 해야 N번째 플레이트(즉, 가장 큰 판) C 기둥으로 이동합니다. 🎜🎜 N-1 플레이트를 B기둥으로 이동합니다. 조건이 맞아야 하기 때문에 큰 것은 하단에 작은 것은 상단에 있으므로 이 N-1 판은 B 기둥에 있습니다. 기둥도 순서대로 있습니다. 🎜🎜마지막으로 이 N-1 플레이트를 B 기둥에서 C 기둥으로 옮겨 최종 목표를 완료하세요. 🎜🎜🎜요약하자면: 🎜🎜🎜첫 번째 단계는 N-1 플레이트를 A에서 B로 옮기는 것입니다. 🎜🎜🎜N-1을 B로 먼저 옮겨야 하는 이유는 무엇인가요? 알다시피, 궁극적으로 달성하는 것은 A에 있는 모든 판을 C로 옮기는 것이기 때문에 순서는 변경할 수 없습니다. 단지 큰 판이 아래쪽에 있고 작은 판이 위쪽에 있을 뿐입니다. 그런 다음 가장 큰 것을 먼저 C로 이동해야 합니다. 그렇지 않으면 조건이 충족되지 않습니다. 🎜🎜가장 큰 접시를 A에서 C로 옮기려면 A에서 가장 큰 접시를 지워야 합니다. 즉, 가장 큰 접시에 있는 모든 접시를 옮겨야 합니다. 그리고 기둥은 3개뿐입니다. C에는 다른 판 손잡이가 없어야 합니다. 그렇지 않으면 이 모든 N-1 판은 B에만 배치할 수 있으며 여전히 순서대로 유지됩니다. 아래 그림이 됩니다. 🎜🎜🎜🎜🎜🎜두 번째 단계는 A의 N번째 플레이트(즉, 가장 큰 플레이트)를 C로 이동하는 것입니다. 🎜🎜<p>가장 큰 접시를 한 번에 A에서 C로 옮기면 됩니다. 아래와 같이: </p>
<p><img src="https://img.php.cn/upload/article/000/000/020/e50df609a8b176f56d217b586766b982-4.png" alt="PHP가 흥미로운 하노이 타워 알고리즘을 구현하는 방법을 분석합니다."></p>
<p><strong>세 번째 단계는 B의 N-1 플레이트를 C로 옮기는 것입니다. </strong></p>
<p>참고: N-1 플레이트를 C로 이동하려면 그 중에서 가장 큰 플레이트를 찾은 다음 가장 큰 플레이트를 먼저 이동해야 합니까? 따라서 여기서는 실제로 1단계와 2단계를 반복하여 N-1 중에서 가장 큰 것을 찾아 먼저 C로 옮기는 문제가 되며 사이클이 반복됩니다. </p>
<p>세 번째 단계는 실제로 요구 사항을 변경하는 것과 동일합니다. K = N - 1. <br>B기둥에는 K판이 있고 A기둥은 비어 있고 C기둥의 판이 가장 크므로 B기둥에 K판이 있으면 비어 있는 것과 같습니다. <br>첫 번째 단계는 B에 있는 K-1 접시를 A로 옮기는 것입니다. <br>두 번째 단계는 B의 K번째 플레이트를 C로 옮기는 것입니다. <br>세 번째 단계는 K-1 접시를 A에서 C로 옮기는 것입니다. <br>...</p>
<p>는 아래 그림이 됩니다</p>
<p>먼저 남은 접시 중 가장 큰 접시를 찾아</p>
<p><img src="https://img.php.cn/upload/article/000/000/020/d1d947b567fd3d8a2295e09c8ff26bf1-5.png" alt=""></p>
<p>그런 다음 가장 큰 접시를 옮깁니다</p>
<p><img src="https://img.php.cn/upload/article/000/000/020/d1d947b567fd3d8a2295e09c8ff26bf1-6.png" alt=""></p>
<p>그런 다음 접시가 하나만 남을 때까지 반복하고, 바로 다음으로 이동합니다. C, 게임이 끝났습니다. </p>
<h3>
<span class="header-link octicon octicon-link"></span>보조기둥</h3>
<p>보조기둥이란 무엇인가요? 이동하려는 플레이트가 모두 A에 있고 목표가 C로 이동하는 것이라고 가정하면 B는 <code>N-1 플레이트의 보조 기둥입니다. 그들은 여기에 일시적으로만 존재할 수 있기 때문에 그렇지 않으면 게임의 규칙을 충족하지 못할 것입니다.
여기서 먼저 보조 기둥을 찾아야 합니다. 구현 방법에 대해 생각하지 말고 먼저 논리를 명확히 하세요.
위의 분석을 통해 이것이 실제로는 순환 내에서 반복적인 작업임을 알 수 있으며, 이는 재귀와 매우 유사하므로 재귀를 사용하여 구현할 수 있습니다.
재귀를 사용하려면 두 가지 필수 조건이 있습니다
1. 재귀 수식을 찾습니다
2. 종료 조건을 찾습니다
종료 조건만 있으면 C필러로 바로 이동해야 합니다. 한 접시.
그럼 재발공식이 뭔가요? 위의 논리적 분석을 바탕으로 3단계로 분해할 수 있다.
첫 번째 단계는 [N-1] 플레이트를 A에서 B로 이동하는 것입니다
두 번째 단계는 [N번째] 플레이트를 A에서 C로 이동하는 것입니다
세 번째 단계는 [남은 플레이트를 이동하는 것입니다. N] -1개] 접시가 B에서 C로 이동되었습니다
다음은 PHP에서 구현한 의사 코드입니다.
class HanoiTower
{
// 计数器
public $count = 0;
/**
* 汉诺塔实现
*
* @param $n 盘子号
* @param $A 初始柱子
* @param $B 中转站
* @param $C 目标柱子
*/
public function hanoi($n, $A, $B, $C)
{
if ($n == 1) {
// 退出条件 只剩一个盘子的时候直接从A移动到C
$this->biggestOne($n, $A, $B, $C);
} else {
// PHP가 흥미로운 하노이 타워 알고리즘을 구현하는 방법을 분석합니다.把 【n-1】 个盘子从A移动到B 此时C为中转站
$this->hanoi($n - 1, $A, $C, $B);
// PHP가 흥미로운 하노이 타워 알고리즘을 구현하는 방법을 분석합니다.把 【第n】 个盘子从A移动到C
$this->biggestOne($n, $A, $B, $C);
// 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
$this->hanoi($n - 1, $B, $A, $C);
}
}
/**
* 移动最大的盘子
* 直接从A移动到C
*/
public function biggestOne($n, $A, $B, $C)
{
++$this->count;
echo '第', $this->count, '步 ', '把 ', $n, '从 ', $A, '移动到', $C, '<br />';
}
}
$n = 5;
$hanoiTower = new HanoiTower();
echo '这是一个有 【', $n, '】 个盘子的汉诺塔：', '<br />';
// 调用执行
$hanoiTower->hanoi($n, 'A', 'B', 'C');
echo '总共需要走：【', $hanoiTower->count, '】 步';결과는 다음과 같습니다.
위 내용은 PHP가 흥미로운 하노이 타워 알고리즘을 구현하는 방법을 분석합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
