C 언어의 정렬 방법은 무엇입니까?
C 언어 정렬 방법은 다음과 같습니다. 1. O(n2) 시간 복잡도를 기반으로 하는 정렬 알고리즘 2. 단순 삽입 정렬 4. A를 기반으로 하는 병합 정렬 병합 작업을 위한 정렬 알고리즘 6. 일종의 분할 정복 방법인 7. 힙 정렬 등

이 튜토리얼의 운영 환경: Windows 7 시스템, C++17 버전, Dell G3 컴퓨터.
1. 선택 정렬 - 단순 선택 정렬
선택 정렬은 O(n2) 시간 복잡도를 기반으로 하는 가장 간단한 정렬 알고리즘입니다. 기본 아이디어는 매번 i=0 위치에서 시작하는 것입니다. 내부 루프는 i 위치에서 n-1 위치까지 가장 작은(가장 큰) 값을 찾습니다.
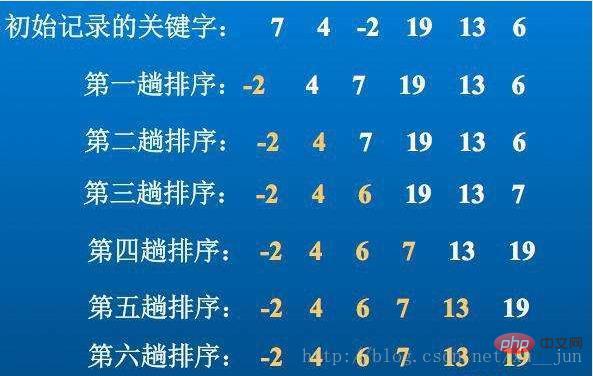
알고리즘 구현:
void selectSort(int arr[], int n)
{ int i, j , minValue, tmp; for(i = 0; i < n-1; i++)
{
minValue = i; for(j = i + 1; j < n; j++)
{ if(arr[minValue] > arr[j])
{
minValue = j;
}
} if(minValue != i)
{
tmp = arr[i];
arr[i] = arr[minValue];
arr[minValue] = tmp;
}
}
}void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n");
}void main()
{ int arr[10] = {2,5,6,4,3,7,9,8,1,0};
printArray(arr, 10);
selectSort(arr, 10);
printArray(arr, 10); return;
}구현에서 볼 수 있듯이 단순 선택 정렬의 복잡성은 O(n2)로 고정됩니다. 각 내부 루프는 정렬되지 않은 시퀀스에서 최소값을 찾은 다음 이를 현재와 교환합니다. 데이터. 선택 정렬은 최대값을 찾아 정렬하기 때문에 루프 수가 거의 고정되어 있습니다. 최적화 방법은 각 루프마다 최대값과 최소값을 동시에 찾는 것입니다. 이렇게 하면 루프 수를 (n/2)로 줄일 수 있습니다. ), 최대값을 기록하기 위해 루프에 추가하기만 하면 원칙은 동일하며 이 기사에서는 더 이상 이 방법을 구현하지 않습니다.
2. 버블 정렬
버블 정렬은 정렬해야 할 배열 그룹에서 두 쌍의 데이터 순서가 필요한 순서와 반대일 때 큰 데이터가 뒤로 이동되도록 데이터를 교환합니다. 각 정렬 패스는 가장 큰 숫자를 이동합니다. 다음과 같이 마지막 위치에 배치합니다.
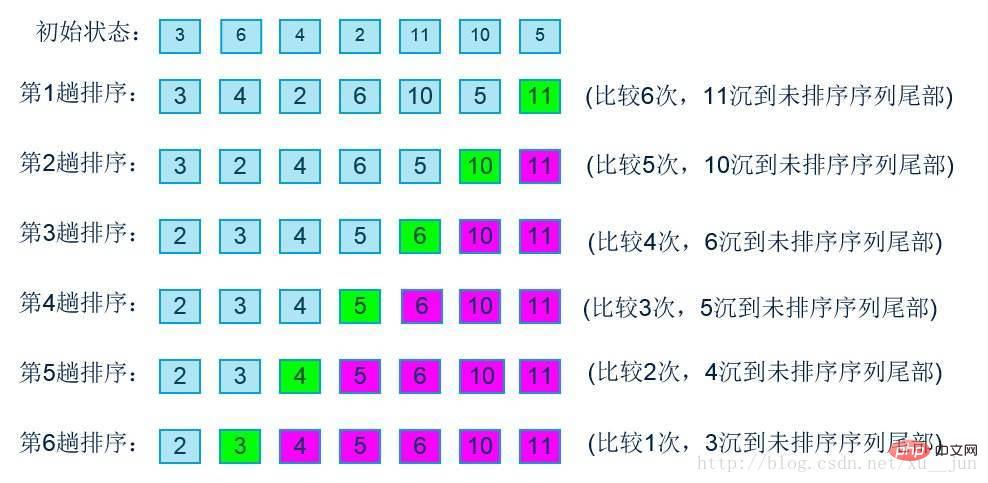
알고리즘 구현:
void bubbleSort(int arr[], int n)
{ int i, j, tmp; for(i = 0; i < n - 1; i++)
{ for(j = 1; j < n; j++)
{ if(arr[j] < arr[j - 1])
{
tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
}
}
}
}void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n");
}void main()
{ int arr[10] = {2,5,6,4,3,7,9,8,1,0};
printArray(arr, 10);
bubbleSort(arr, 10);
printArray(arr, 10); return;
}위는 가장 간단한 구현 방법입니다. 주의해야 할 것은 경계 문제일 수 있습니다. i, j. 이 방법은 사이클 수를 고정하므로 다양한 상황을 해결할 수 있지만 알고리즘의 목적은 효율성을 향상시키는 것입니다. 버블 정렬의 프로세스 다이어그램에 따르면 이 알고리즘은 다음과 같습니다. 최소 두 지점에서 최적화됨:
1) 외부 루프의 경우 현재 시퀀스가 이미 순서대로 되어 있으면 교환이 수행되지 않으며 다음 사이클이 직접 점프 아웃되어야 합니다.
2) 내부 루프 이후의 최대값이 이미 순서대로 지정되면 더 이상 루프를 수행해서는 안 됩니다.
최적화된 코드 구현:
void bubbleSort_1(int arr[], int n)
{ int i, nflag, tmp; do
{
nflag = 0; for(i = 0; i < n - 1; i++)
{ if(arr[i] > arr[i + 1])
{
tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
nflag = i + 1;
}
}
n = nflag;
}while(nflag);
}위와 같이 nflag가 0이면 이번 주기에서 교환이 발생하지 않았음을 의미하며 시퀀스가 이미 순서대로 되어 있고 nflag>0인 경우 재활용할 필요가 없다는 의미입니다. 마지막 교환이 기록되고 이 위치는 나중에 사용되며 시퀀스는 모두 순서대로 이루어지며 루프는 더 이상 진행되지 않습니다.
3. 삽입 정렬 - 단순 삽입 정렬
삽입 정렬은 이미 정렬된 시퀀스에 레코드를 삽입하고 새 요소에 1을 더한 정렬된 시퀀스를 얻는 것입니다. 구현 시 첫 번째 요소는 정렬된 시퀀스로 간주됩니다. , 두 번째 요소부터 하나씩 삽입하여 완전한 순서의 시퀀스를 얻습니다. 삽입 과정은 다음과 같습니다.
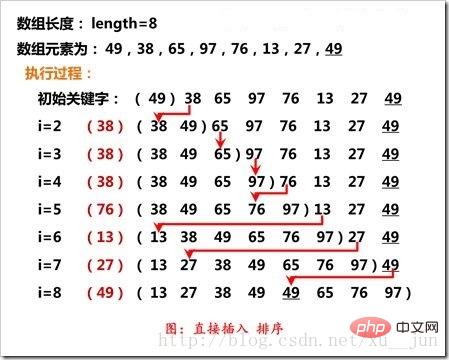
그림에 표시된 대로 삽입 정렬의 i번째 요소는 인접한 이전 요소와 비교됩니다. .정렬 순서와 비교하면 반대로 이전 요소와 위치를 교환하여 해당 위치까지 반복합니다.
알고리즘 구현:
void insertSort(int arr[], int n)
{ int i, j, tmp; for(i = 1; i < n; i++)
{ for(j = i; j > 0; j--)
{ if(arr[j] < arr[j-1])
{
tmp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = tmp;
} else
{ break;
}
}
} return;
}void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n"); return;
}void main()
{ int arr[10] = {2,5,6,4,3,7,9,8,1,0};
printArray(arr, 10);
insertSort(arr, 10);
printArray(arr, 10); return;
}위에서 언급했듯이 선택 정렬은 어떠한 경우에도 O(n2) 알고리즘으로 고정됩니다. 삽입 알고리즘도 O(n2) 알고리즘이지만 이미 정렬되어 있는 경우에는 의 경우 삽입이 루프에서 직접 벗어날 수 있습니다. 극단적인 경우(완전히 정렬된) 삽입 정렬은 O(n) 알고리즘일 수 있습니다. 그러나 실제 완전히 비순차적인 테스트 사례에서는 본 논문의 선택 정렬과 비교하여 동일한 순서의 경우 삽입 정렬의 실행 시간이 선택 정렬의 실행 시간보다 길다는 것을 알 수 있다. 선택 정렬의 각 외부 루프는 선택한 가장 많은 값만 교환하는 반면, 삽입 정렬은 적절한 위치를 알기 위해 인접한 요소와의 지속적인 교환이 필요하기 때문에 교환의 세 가지 할당 작업도 실행 시간에 영향을 미치므로 이 점은 아래 최적화:
최적화 구현 후:
void insertSort_1(int arr[], int n)
{ int i, j, tmp, elem; for(i = 1; i < n; i++)
{
elem = arr[i]; for(j = i; j > 0; j--)
{ if(elem < arr[j-1])
{
arr[j] = arr[j-1];
} else
{ break;
}
}
arr[j] = elem;
} return;
}Optimization 코드는 삽입해야 할 값을 캐시하고 삽입 위치 뒤의 요소를 하나씩 뒤로 이동하며 교환의 할당 3개를 하나의 할당으로 변경하여 실행을 줄입니다. 시간.
4. 삽입 정렬 - Hill 정렬
Hill 정렬의 기본 아이디어는 먼저 n보다 작은 정수 d1을 첫 번째 증분으로 가져와 모든 요소를 그룹화하는 것입니다. 거리가 d1의 배수인 모든 레코드는 동일한 그룹에 배치됩니다. 먼저 각 그룹 내에서 직접 삽입 정렬을 수행한 다음 두 번째 증분 d2 < d1을 취하고 증분 = 1( < ...< d2 < d1)이 될 때까지 위의 그룹화 및 정렬을 반복합니다. 직접 삽입 정렬을 위해 레코드를 동일한 그룹에 배치하는 경우 Hill 정렬은 삽입 정렬의 다음 두 가지 속성을 기반으로 삽입 정렬을 주로 개선합니다.
1) 삽입 정렬은 거의 이미 정렬된 데이터에 대해 작동합니다. 선형 정렬의 효율성을 높일 수 있습니다.
2)但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
排序过程如下:
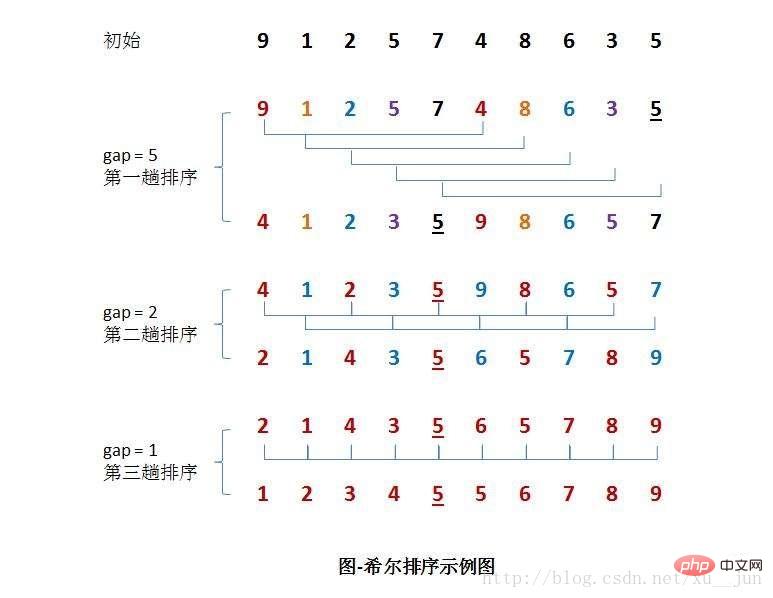
算法实现:基于一种简单的增量分组方式{n/2,n/4,n/8……,1}
void shellSort(int arr[], int n)
{ int i, j, elem; int k = n/2; while(k>=1)
{ for(i = k; i < n; i ++)
{
elem = arr[i]; for(j = i; j >= k; j-=k)
{ if(elem < arr[j-k])
{
arr[j] = arr[j-k];
} else
{ break;
}
}
arr[j] = elem;
}
k = k/2;
}
}void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n"); return;
}void main()
{ int arr[10] = {2,5,6,4,3,7,9,8,1,0};
printArray(arr, 10);
shellSort(arr, 10);
printArray(arr, 10); return;
}5.归并排序
归并排序是基于归并操作的一种排序算法,归并操作的原理就是将一组有序的子序列合并成一个完整的有序序列,即首先需要把一个序列分成多个有序的子序列,通过分解到每个子序列只有一个元素时,每个子序列都是有序的,在通过归并各个子序列得到一个完整的序列。
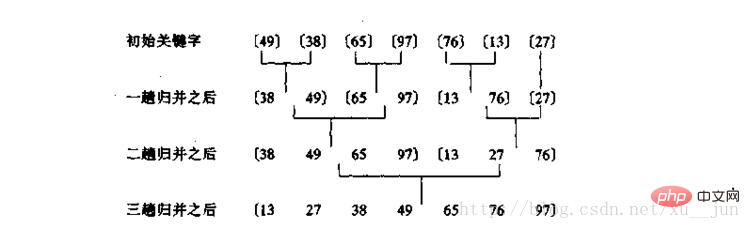
合并过程:
把序列中每个单独元素看作一个有序序列,每两个单独序列归并为一个具有两个元素的有序序列,每两个有两个元素的序列归并为一个四个元素的序列依次类推。两个序列归并为一个序列的方式:因为两个子序列都是有序的(假设由小到大),所有每个子序列最左边都是序列中最小的值,整个序列最小值只需要比较两个序列最左边的值,所以归并的过程不停取子序列最左边值中的最小值放到新的序列中,两个子序列值取完后就得到一个有序的完整序列。
归并的算法实现:
void merge(int arr[], int l, int mid, int r)
{ int len,i, pl, pr; int *tmp = NULL;
len = r - l + 1;
tmp = (int*)malloc(len * sizeof(int)); //申请存放完整序列内存
memset(tmp, 0x0, len * sizeof(int));
pl = l;
pr = mid + 1;
i = 0; while(pl <= mid && pr <= r) //两个子序列都有值,比较最小值
{ if(arr[pl] < arr[pr])
{
tmp[i++] = arr[pl++];
} else
{
tmp[i++] = arr[pr++];
}
} while(pl <= mid) //左边子序列还有值,直接拷贝到新序列中
{
tmp[i++] = arr[pl++];
} while(pr <= r) //右边子序列还有值
{
tmp[i++] = arr[pr++];
} for(i = 0; i < len; i++)
{
arr[i+l] = tmp[i];
} free(tmp); return;
}归并的迭代算法:
迭代算法如上面所说,从单个元素开始合并,子序列长度不停增加直到得到一个长度为n的完整序列。
#include<stdio.h>#include<stdlib.h>#include<string.h>void merge(int arr[], int l, int mid, int r)
{ int len,i, pl, pr; int *tmp = NULL;
len = r - l + 1;
tmp = (int*)malloc(len * sizeof(int)); //申请存放完整序列内存
memset(tmp, 0x0, len * sizeof(int));
pl = l;
pr = mid + 1;
i = 0; while(pl <= mid && pr <= r) //两个子序列都有值,比较最小值
{ if(arr[pl] < arr[pr])
{
tmp[i++] = arr[pl++];
} else
{
tmp[i++] = arr[pr++];
}
} while(pl <= mid) //左边子序列还有值,直接拷贝到新序列中
{
tmp[i++] = arr[pl++];
} while(pr <= r) //右边子序列还有值
{
tmp[i++] = arr[pr++];
} for(i = 0; i < len; i++)
{
arr[i+l] = tmp[i];
} free(tmp); return;
}int min(int x, int y)
{ return (x > y)? y : x;
}/*
归并完成的条件是得到子序列长度等于n,用sz表示当前子序列的长度。从1开始每次翻倍直到等于n。根据上面归并的方法,从i=0开始分组,下一组坐标应该i + 2*sz,第i组第一个元素为arr[i],最右边元素应该为arr[i+2*sz -1],遇到序列最右边元素不够分组的元素个数时应该取n-1,中间的元素为arr[i+sz -1],依次类推进行归并得到完整的序列
*/void mergeSortBu(int arr[], int n)
{ int sz, i, mid,l, r; for(sz = 1; sz < n; sz+=sz)
{ for(i = 0; i < n - sz; i += 2*sz)
{
l = i;
r = i + sz + sz;
mid = i + sz -1;
merge(arr, l, mid, min(r-1, n-1));
}
} return;
}void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n"); return;
}void main()
{ int arr[10] = {2,5,6,4,3,7,9,8,1,0};
printArray(arr, 10);
mergeSortBu(arr, 10);
printArray(arr, 10); return;
}另一种是通过递归的方式,递归方式可以理解为至顶向下的操作,即先将完整序列不停分解为子序列,然后在将子序列归并为完整序列。
递归算法实现:
void mergeSort(int arr[], int l, int r)
{ if(l >= r)
{
return;
} int mid = (l + r)/2;
mergeSort(arr, l, mid);
mergeSort(arr, mid+1, r);
merge(arr, l, mid, r);
return;
}对于归并算法大家可以考虑到由于子序列都是有序的,所有如果左边序列的最大值都比右边序列的最小值小,那么整个序列就是有序的,不需要进行merge操作,因此可以在每次merge操作加一个if(arr[mid] > arr[mid+1])判断进行优化,这种优化对于近乎有序的序列非常有效果,不过对于一般的情况会有一次判断的额外开销,可以根据具体情况处理。
6.快速排序
快速排序跟归并排序类似属于分治法的一种,基本思想是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
排序过程如图:
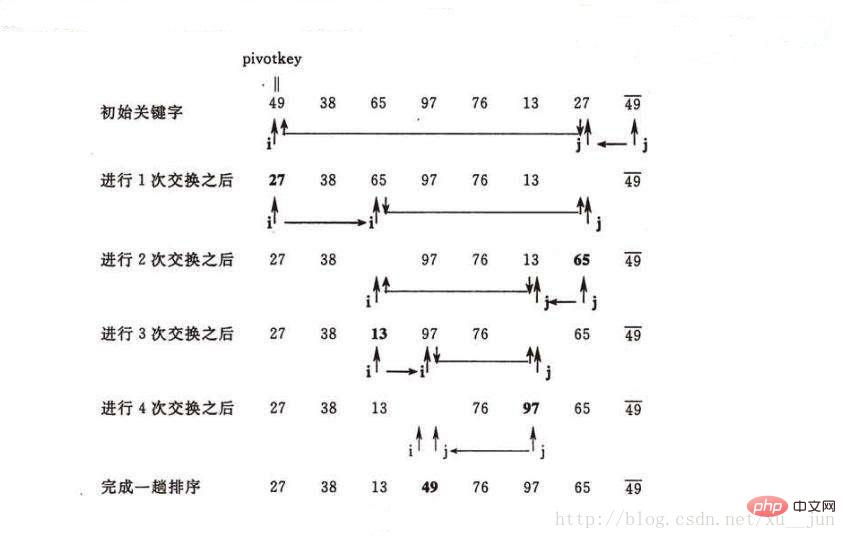
因此,快速排序每次排序将一个序列分为两部分,左边部分都小于等于右边部分,然后在递归对左右两部分进行快速排序直到每部分元素个数为1时则整个序列都是有序的,因此快速排序主要问题在怎样将一个序列分成两部分,其中一部分所有元素都小于另一部分,对于这一块操作我们叫做partition,原理是先选取序列中的一个元素做参考量,比它小的都放在序列左边,比它大的都放在序列右边。
算法实现:
快速排序-单路快排:
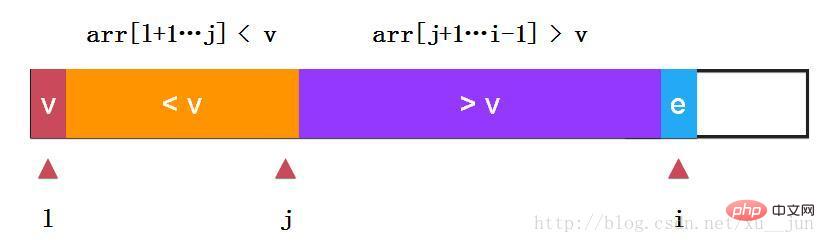
如上:我们选取第一个元素v作为参考量及arr[l],定义j变量为两部分分割哨兵,变量i从l+1开始遍历每个变量,如果当前变量e > v则i++检测下一个元素,如果当前变量e < v 则e与arr[j+1]交换,可以看到arr[j+1]由交换前大于v变成小于v arr[i]变成大于v,同时对i++,j++,始终保持:arr[l+1….j] < v, arr[j+1….i-1] > v
代码实现:
#include <stdio.h>void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n"); return;
}void swap(int *a, int *b)
{ int tmp;
tmp = *a;
*a = *b;
*b = tmp; return;
}//arr[l+1...j] < arr[l], arr[j+1,..i)>arr[l]static int partition(int arr[], int l, int r)
{ int i, j;
i = l + 1;
j = l; while(i <= r)
{ if(arr[i] > arr[l])
{
i++;
} else
{
swap(&arr[j + 1], &arr[i]);
i++;
j++;
}
}
swap(&arr[l], &arr[j]); return j;
}static void _quickSort(int arr[], int l, int r)
{ int key; if(l >= r)
{ return;
}
key = partition(arr, l, r);
_quickSort(arr, l, key - 1);
_quickSort(arr, key + 1, r);
}void quickSort(int arr[], int n)
{
_quickSort(arr, 0, n - 1); return;
}void main()
{ int arr[10] = {1,5,9,8,7,6,3,4,0,2};
printArray(arr, 10);
quickSort(arr, 10);
printArray(arr, 10);
}因为有变量i从左到右依次遍历序列元素,所有这种方式叫单路快排,不过细心的同学可以发现我们忽略了考虑e等于v的情况,这种快排方式一大缺点就是对于高重复率的序列即大量e等于v的情况会退化为O(n2)算法,原因在大量e等于v的情况划分情况会如下图两种情况:
 解决这种问题的一另种方法:
解决这种问题的一另种方法:
快速排序-两路快排:
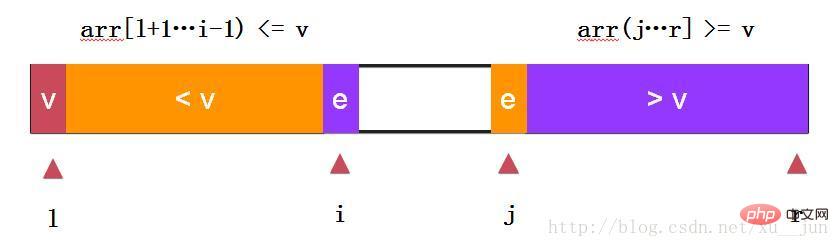
两路快排通过i和j同时向中间遍历元素,e==v的元素分布在左右两个部分,不至于在多重复元素时划分严重失衡。依旧去第一个元素arr[l]为参考量,始终保持arr[l+1….i) <= arr[l], arr(j…r] >=arr[l]原则.
代码实现:
//arr[l+1....i) <=arr[l], arr(j...r] >=arr[l]static int partition2(int arr[], int l, int r)
{ int i, j;
i = l + 1 ;
j = r; while(i <= j)
{ while(i <= j && arr[j] > arr[l]) /*注意arr[j] >arr[l] 不是arr[j] >= arr[l]*/
{
j--;
} while(i <= j && arr[i] < arr[l])
{
i++;
} if(i < j)
{
swap(&arr[i], &arr[j]);
i++;
j--;
}
}
swap(&arr[j],&arr[l]); return j;
}针对重复元素比较多的情况还有一种实现方式:
快速排序-三路快排:
三路快排是在两路快排的基础上对e==v的情况做单独的处理,对于重复元素非常多的情况优势很大:
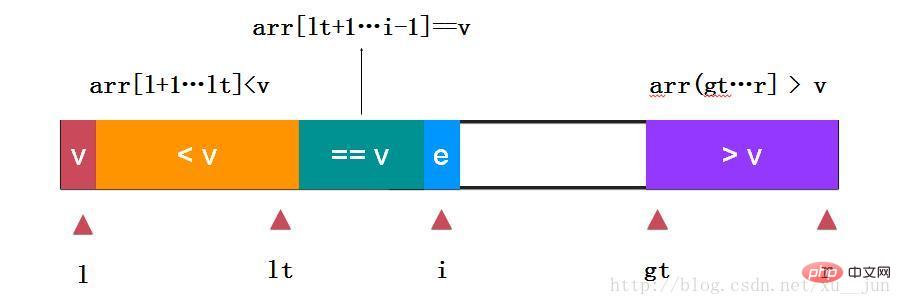
如上:取arr[l]为参考量,定义变量lt为小于v和等于v的分割点,变量i为遍历指针,gt为大于v和未遍历元素分割点,gt指向未遍历元素,边界条件跟个人定义有关本文始终保持arr[l+1…lt] < v,arr[lt+1….i-1],arr(gt…..r]>v的状态。
代码实现:
#include <stdio.h>void printArray(int arr[], int n)
{ int i; for(i = 0; i < n; i++)
{ printf("%d ", arr[i]);
} printf("\n"); return;
}
void swap(int *a, int *b)
{ int tmp;
tmp = *a; *a = *b; *b = tmp; return;
}
static void _quickSort3(int arr [ ],int l,int r)
{ int i, lt, gt; if(l >= r)
{ return;
}
i = l + 1; lt = l; gt = r ; while(i <= gt)
{ if(arr[i] < arr[l])
{
swap(&arr[lt + 1], &arr[i]); lt ++;
i++;
} else if(arr[i] > arr[l])
{
swap(&arr[i], &arr[gt]); gt--;
} else
{
i++;
}
}
swap(&arr[l], &arr[gt]);
_quickSort3(arr, l, lt);
_quickSort3(arr, gt + 1, r); return;
}
void quickSort(int arr[], int n)
{
_quickSort3(arr, 0, n - 1); return;
}
void main()
{ int arr[10] = {1,5,9,8,7,6,3,4,0,2};
printArray(arr, 10);
quickSort(arr, 10);
printArray(arr, 10);
}三路快排在重复率比较高的情况下比前两种有较大优势,但就完全随机情况略差于两路快排,可以根据具体情况进行合理选择,另外本文在选取参考值时为了方便一直选择第一个元素为参考值,这种方式对于近乎有序的序列算法会退化到O(n2),因此一般选取参考值可以随机选择参考值或者其他选择参考值的方法然后再与arr[l]交换,依旧可以使用相同的算法。
7.堆排序
堆其实一种树形结构,以二叉堆为例,是一颗完全二叉树(即除最后一层外每个节点都有两个子节点,且非满的二叉树叶节点都在最后一层的左边位置),二叉树满足每个节点都大于等于他的子节点(大顶堆)或者每个节点都小于等于他的子节点(小顶堆),根据堆的定义可以得到堆满足顶点一定是整个序列的最大值(大顶堆)或者最小值(小顶堆)。如下图:
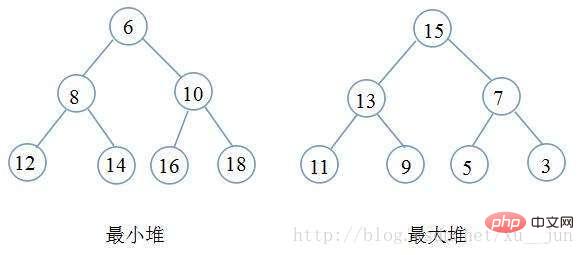
堆排序就是一种基于堆得选择排序,先将需要排序的序列构建成堆,在每次选取堆顶点的最大值和最小值知道完成整个堆的遍历。
用数组表示堆:
二叉堆作为树的一种,通常用结构体表示,为了排序的方便,我们通常使用数组来表示堆,如下图:
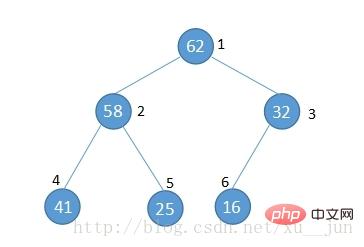
将一个堆按图中的方式按层编号可以得到如下结论:
1)节点的父节点编号满足parent(i) = i/2
2)节点的左孩子编号满足 left child (i) = 2*i
3)节点右孩子满足 right child (i) = 2*i + 1
由于数组编号是从0开始对上面结论修改得到:
parent(i) = (i-1)/2
left child (i) = 2*i + 1
right child (i) = 2*i + 2
堆的两种操作方式:
根据堆的主要性质(父节点大于两个子节点或者小于两个子节点),可以得到堆的两种主要操作方式,以大顶堆为例:
a)如果子节点大于父节点将子节点上移(shift up)
b)如果父节点小于两个子节点中的最大值则父节点下移(shift down)
shift up:
如果往已经建好的堆中添加一个元素,如下图,此时不再满足堆的性质,堆遭到破坏,就需要执行shift up 操作将添加的元素上移调整直到满足堆的性质。
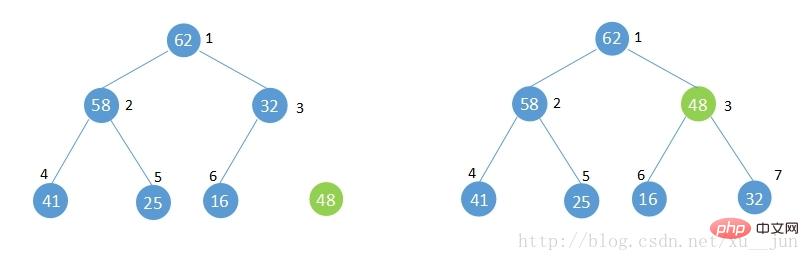
调整堆的方法:
1)7号位新增元素48与其父节点[i/2]=3比较大于父节点的32不满足堆性质,将其与父节点交换。
2)此时新增元素在3号位,再与3号位父节点[i/2]=1比较,小于1号位的62满足堆性质,不再交换,如果此步骤依旧不满足堆性质则重复1步骤直到满足堆的性质或者到根节点。
3)堆调整完成。
代码实现:
代码中基于数组实现,数组下表从0开始,父子节点关系如用数组表示堆
/*parent(i) = (i-1)/2
left child (i) = 2*i + 1
right child (i) = 2*i + 2*/void swap(int *a, int *b)
{ int tmp;
tmp = *a; *a = *b; *b = tmp; return;
}
void shiftUp(int arr[], int n, int k)
{ while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2])
{
swap(&arr[k], &arr[(k-1)/2]);
k = (k - 1)/2;
} return;
}shift down:
与shift up相反,如果从一个建好的堆中删除一个元素,此时不再满足堆的性质,此时应该怎样来调整堆呢? 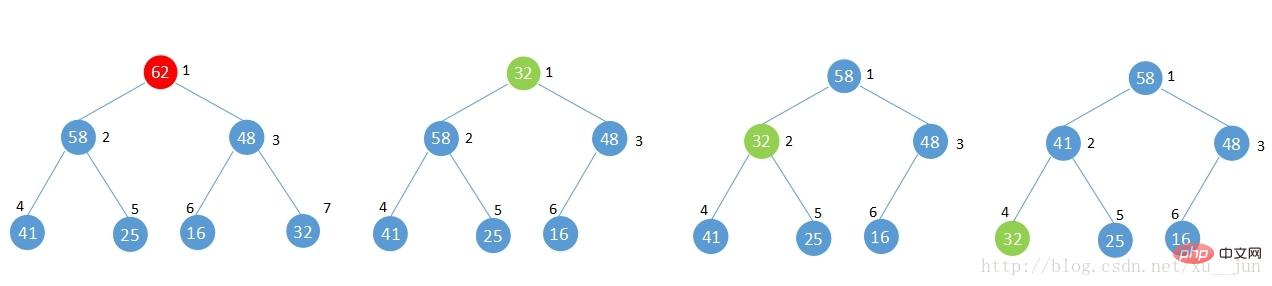
如上图,将堆中根节点元素62删除调整堆的步骤为:
1)将最后一个元素移到删除节点的位置
2)与删除节点两个子节点中较大的子节点比较,如果节点小于较大的子节点,与子节点交换,否则满足堆性质,完成调整。
3)重复步骤2,直到满足堆性质或者已经为叶节点。
4)完成堆调整
代码实现:
void shiftDown(int arr[], int n, int k)
{ int j = 0 ; while(2*k + 1 < n)
{
j = 2 *k + 1; //标记两个子节点较大的节点,初始为左节点
if (j + 1 < n && arr[j] < arr[j+1])
{
j ++;
} if(arr[k] < arr[j])
{
swap(&arr[k], &arr[j]);
k = j;
} else
{ break;
}
} return;
}知道了上面两种堆的操作后,堆排序的过程就非常简单了
1)首先将待排序序列建成堆,由于最后一层即叶节点没有子节点所以可以看成满足堆性质的节点,第一个可能出现不满足堆性质的节点在第一个父节点的位置,假设最后一个叶子节点为(n - 1) 则第一个父节点位置为(n-1-1)/2,只需要依次对第一个父节点之前的节点执行shift down操作到根节点后建堆完成。
2)建堆完成后(以大顶堆为例)第一个元素arr[0]必定为序列中最大值,将最大值提取出来(与数组最后一个元素交换),此时堆不再满足堆性质,再对根节点进行shift down操作,依次循环直到根节点,排序完成。
代码实现:
#include/*parent(i) = (i-1)/2 left child (i) = 2*i + 1 right child (i) = 2*i + 2*/void swap(int *a, int *b) { int tmp; tmp = *a; *a = *b; *b = tmp; return; } void shiftUp(int arr[], int n, int k) { while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2]) { swap(&arr[k], &arr[(k-1)/2]); k = (k - 1)/2; } return; } void shiftDown(int arr[], int n, int k) { int j = 0 ; while(2*k + 1 < n) { j = 2 *k + 1; if (j + 1 < n && arr[j] < arr[j+1]) { j ++; } if(arr[k] < arr[j]) { swap(&arr[k], &arr[j]); k = j; } else { break; } } return; } void heapSort(int arr[], int n) { int i = 0; for(i = (n - 1 -1)/2; i >=0; i--) { shiftDown(arr, n, i); } for(i = n - 1; i > 0; i--) { swap(&arr[0], &arr[i]); shiftDown(arr, i, 0); } return; } void printArray(int arr[], int n) { int i; for(i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); return; } void main() { int arr[10] = {1,5,9,8,7,6,3,4,0,2}; printArray(arr, 10); heapSort(arr, 10); printArray(arr, 10); }
推荐教程:《C#》
위 내용은 C 언어의 정렬 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7494
7494
 15
15
 1377
1377
 52
52
 77
77
 11
11
 52
52
 19
19
 19
19
 49
49
 C 언어로 특수 문자를 처리하는 방법
Apr 03, 2025 pm 03:18 PM
C 언어로 특수 문자를 처리하는 방법
Apr 03, 2025 pm 03:18 PM
C 언어에서 특수 문자는 다음과 같은 탈출 시퀀스를 통해 처리됩니다. \ n 라인 브레이크를 나타냅니다. \ t는 탭 문자를 의미합니다. char c = '\ n'과 같은 특수 문자를 나타 내기 위해 탈출 시퀀스 또는 문자 상수를 사용하십시오. 백 슬래시는 두 번 탈출해야합니다. 다른 플랫폼과 컴파일러마다 다른 탈출 시퀀스가있을 수 있습니다. 문서를 참조하십시오.
 C 현에서 숯의 역할은 무엇입니까?
Apr 03, 2025 pm 03:15 PM
C 현에서 숯의 역할은 무엇입니까?
Apr 03, 2025 pm 03:15 PM
C에서 숯 유형은 문자열에 사용됩니다. 1. 단일 문자를 저장하십시오. 2. 배열을 사용하여 문자열을 나타내고 널 터미네이터로 끝납니다. 3. 문자열 작동 함수를 통해 작동합니다. 4. 키보드에서 문자열을 읽거나 출력하십시오.
 C 언어로 다양한 기호를 사용하는 방법
Apr 03, 2025 pm 04:48 PM
C 언어로 다양한 기호를 사용하는 방법
Apr 03, 2025 pm 04:48 PM
C 언어 커버 산술, 할당, 조건, 논리, 비트 연산자 등의 기호의 사용 방법은 기본 수학 연산에 사용되며, 할당 연산자는 할당 및 추가, 곱하기, 분할 할당에 사용되며, 곱하기 및 분할 할당에 사용되며, 조건에 따라 조건 운영자가 사용되며, 비트 오퍼레이터에 사용되며, 스페셜 오퍼레이터는 비트 수준의 운영에 사용됩니다. 포인터, 파일 종료 마커 및 비수통 값.
 멀티 스레딩과 비동기 C#의 차이
Apr 03, 2025 pm 02:57 PM
멀티 스레딩과 비동기 C#의 차이
Apr 03, 2025 pm 02:57 PM
멀티 스레딩과 비동기식의 차이점은 멀티 스레딩이 동시에 여러 스레드를 실행하는 반면, 현재 스레드를 차단하지 않고 비동기식으로 작업을 수행한다는 것입니다. 멀티 스레딩은 컴퓨팅 집약적 인 작업에 사용되며 비동기식은 사용자 상호 작용에 사용됩니다. 멀티 스레딩의 장점은 컴퓨팅 성능을 향상시키는 것이지만 비동기의 장점은 UI 스레드를 차단하지 않는 것입니다. 멀티 스레딩 또는 비동기식을 선택하는 것은 작업의 특성에 따라 다릅니다. 계산 집약적 작업은 멀티 스레딩을 사용하고 외부 리소스와 상호 작용하고 UI 응답 성을 비동기식으로 유지 해야하는 작업을 사용합니다.
 C 언어에서 Char와 WCHAR_T의 차이
Apr 03, 2025 pm 03:09 PM
C 언어에서 Char와 WCHAR_T의 차이
Apr 03, 2025 pm 03:09 PM
C 언어에서 char와 wchar_t의 주요 차이점은 문자 인코딩입니다. char ascii를 사용하거나 ascii를 확장하고, wchar_t는 유니 코드를 사용합니다. Char는 1-2 바이트를 차지하고 WCHAR_T는 2-4 바이트를 차지합니다. Char는 영어 텍스트에 적합하며 WCHAR_T는 다국어 텍스트에 적합합니다. Char_t는 널리 지원되며, 컴파일러 및 운영 체제가 유니 코드를 지원하는지 여부에 따라 다릅니다. Char는 문자 범위가 제한되며 WCHAR_T는 더 큰 문자 범위를 가지며 특수 함수는 산술 작업에 사용됩니다.
 C 언어로 Char를 변환하는 방법
Apr 03, 2025 pm 03:21 PM
C 언어로 Char를 변환하는 방법
Apr 03, 2025 pm 03:21 PM
C 언어에서 숯 유형 변환은 다른 유형으로 직접 변환 할 수 있습니다. 캐스팅 : 캐스팅 캐릭터 사용. 자동 유형 변환 : 한 유형의 데이터가 다른 유형의 값을 수용 할 수 있으면 컴파일러가 자동으로 변환됩니다.
 C 언어로 Char Array를 사용하는 방법
Apr 03, 2025 pm 03:24 PM
C 언어로 Char Array를 사용하는 방법
Apr 03, 2025 pm 03:24 PM
char 어레이는 문자 시퀀스를 C 언어로 저장하고 char array_name [size]로 선언됩니다. 액세스 요소는 첨자 연산자를 통해 전달되며 요소는 문자열의 끝점을 나타내는 널 터미네이터 '\ 0'으로 끝납니다. C 언어는 strlen (), strcpy (), strcat () 및 strcmp ()와 같은 다양한 문자열 조작 함수를 제공합니다.
 C 언어 합계의 기능은 무엇입니까?
Apr 03, 2025 pm 02:21 PM
C 언어 합계의 기능은 무엇입니까?
Apr 03, 2025 pm 02:21 PM
C 언어에는 내장 합계 기능이 없으므로 직접 작성해야합니다. 합계는 배열 및 축적 요소를 가로 질러 달성 할 수 있습니다. 루프 버전 : 루프 및 배열 길이를 사용하여 계산됩니다. 포인터 버전 : 포인터를 사용하여 배열 요소를 가리키며 효율적인 합계는 자체 증가 포인터를 통해 달성됩니다. 동적으로 배열 버전을 할당 : 배열을 동적으로 할당하고 메모리를 직접 관리하여 메모리 누출을 방지하기 위해 할당 된 메모리가 해제되도록합니다.




