파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?-파이썬 튜토리얼-php.cn

이 글에서는 python에 대한 관련 지식을 제공합니다. 이 글에서는 두 개의 스택을 사용하여 큐를 구현하는 방법, 두 개의 큐를 사용하여 스택을 구현하는 방법, 스택 등 큐 관련 응용 연습을 주로 소개합니다. 요소의 연속성 판단, 등 모든 분들께 도움이 되었으면 좋겠습니다.

파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

0. 학습 목표

우리는 대기열의 관련 개념과 구현을 배웠고 실제 문제에서 대기열의 광범위한 적용도 이해했습니다. 대기열 관련 연습을 통해 대기열에 대한 이해를 더욱 심화시키는 동시에 대기열을 사용하여 일부 복잡한 문제를 해결하는 데 소요되는 시간 복잡성을 줄일 수 있습니다.

1. 두 개의 스택을 사용하여 대기열을 구현합니다

[질문] 두 개의 스택이 주어지면 스택의 기본 연산만 사용하여 대기열을 구현합니다.

[아이디어] 이 문제를 해결하는 열쇠는 스택의 반전 기능에 있습니다. 스택에 푸시된 일련의 요소는 스택에서 팝될 때 역순으로 반환됩니다. 따라서 두 개의 스택을 사용하면 동일한 순서로 요소를 반환할 수 있습니다. 요소의 역순은 원래 순서를 얻기 위해 다시 역순으로 이루어집니다. 구체적인 작업은 아래 그림에 나와 있습니다.

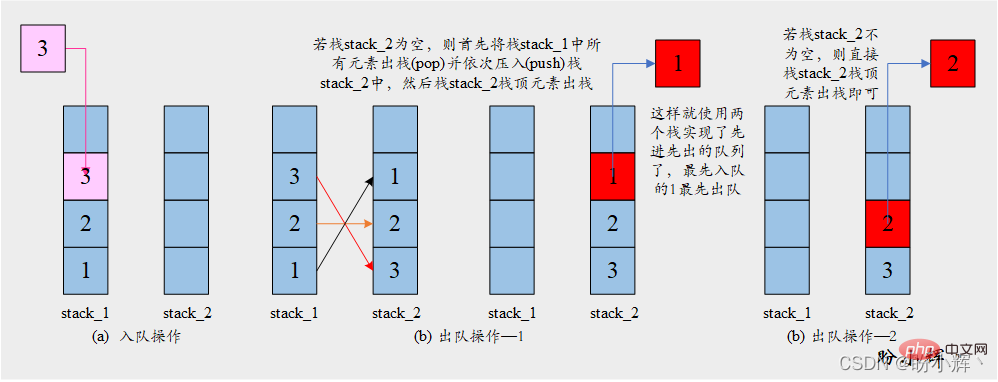
파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

[알고리즘]

Enqueueenqueue:
요소를 스택에 푸시stack_1
queue 대기열에서 제거:
stack_2 스택이 비어 있지 않은 경우:
stack_2 대기열에서 최상위 요소 팝 스택
그렇지 않은 경우:
stack_1에서 모든 요소를 팝하고 stack_2로 푸시
stack_2 스택의 최상위 요소를 팝합니다 enqueue：
将元素推入栈 stack_1
出队 dequeue：
如果栈 stack_2 不为空：
stack_2 栈顶元素出栈
否则：
将所有元素依次从 stack_1 弹出并压入 stack_2
stack_2 栈顶元素出栈

[代码]

class Queue:
    def __init__(self):
        self.stack_1 = Stack()
        self.stack_2 = Stack()
    def enqueue(self, data):
        self.stack_1.push(data)
    def dequeue(self):
        if self.stack_2.isempty():
            while not self.stack_1.isempty():
                self.stack_2.push(self.stack_1.pop())
        return self.stack_2.pop()

로그인 후 복사

[时空复杂度] 入队时间复杂度为 $O (1)$ ，如果栈 stack_2 不为空，那么出队的时间复杂度为 $O (1)$ ，如果栈 stack_2 为空，则需要将元素从 stack_1 转移到 stack_2，但由于 stack_2 中转移的元素数量和出队的元素数量是相等的，因此出队的摊销时间复杂度为 $O (1)$ 。

2. 파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

[问题] 给定两个队列，仅使用队列的基本操作实现一个栈。

[思路] 由于队列并不具备反转顺序的特性，入队顺序即为元素的出队顺序。因此想要获取最后一个入队的元素，需要首先将之前所有元素出队。因此为了使用两个队列实现栈，我们需要将其中一个队列 store_queue 用于存储元素，另一个队列 temp_queue 则用来保存为了获取最后一个元素而保存临时出队的元素。push 操作将给定元素入队到存储队列 store_queue 中；pop 操作首先把存储队列 store_queue 中除最后一个元素外的所有元素都转移到临时队列 temp_queue 中，然后存储队列 store_queue

[Code]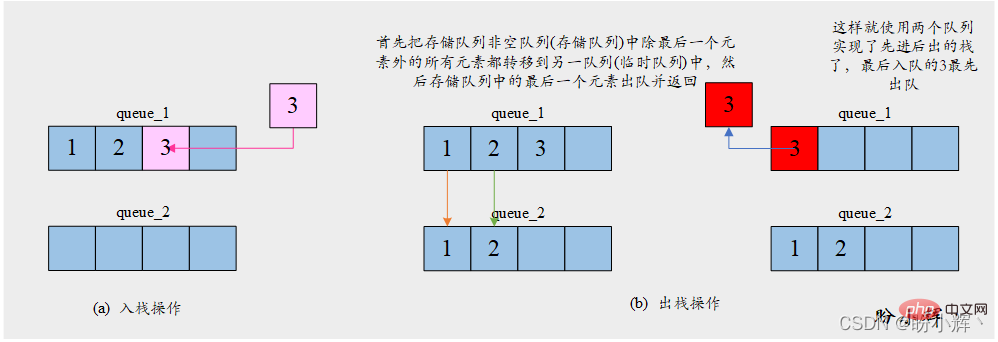 파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

class Stack:
    def __init__(self):
        self.queue_1 = Queue()
        self.queue_2 = Queue()
    def isempty(self):
        return self.queue_1.isempty() and self.queue_2.isempty()
    def push(self, data):
        if self.queue_2.isempty():
            self.queue_1.enqueue(data)
        else:
            self.queue_2.enqueue(data)
    def pop(self):
        if self.isempty():
            raise IndexError("Stack is empty")
        elif self.queue_2.isempty():
            while not self.queue_1.isempty():
                p = self.queue_1.dequeue()
                if self.queue_1.isempty():
                    return p
                self.queue_2.enqueue(p)
        else:
            while not self.queue_2.isempty():
                p = self.queue_2.dequeue()
                if self.queue_2.isempty():
                    return p
                self.queue_1.enqueue(p)

로그인 후 복사

[Time and Space Complexity] 대기열에 넣기의 시간 복잡도는 $O (1), stack_2 스택이 비어 있지 않은 경우 대기열 제거의 시간 복잡도는 입니다. O (1) span> stack_2 스택이 비어 있으므로 요소를 stack_1 에서 stack_2 로 전송해야 하지만 stack_2 에 전송된 요소 수와 대기열에서 제거된 요소의 수가 동일하므로 대기열 제거의 분할 시간 복잡도는 O (1) .$

🎜2. 두 개의 큐를 사용하여 스택을 구현합니다🎜🎜🎜[질문]🎜 두 개의 큐가 주어지면 큐의 기본 연산만 사용하여 스택을 구현합니다. 🎜🎜🎜[아이디어]🎜 큐에는 순서를 바꾸는 기능이 없으므로 요소가 큐에 추가되는 순서는 요소가 큐에서 제거되는 순서입니다. 따라서 마지막 요소를 대기열에 추가하려면 먼저 이전 요소를 모두 대기열에서 제거해야 합니다. 따라서 두 개의 대기열을 사용하여 스택을 구현하려면 store_queue 대기열 중 하나를 사용하여 요소를 저장하고 다른 대기열 temp_queue를 사용하여 요소를 저장해야 합니다. 일시적으로 대기열에서 제거된 요소를 가져옵니다. push 작업은 지정된 요소를 저장소 대기열 store_queue에 추가합니다. pop 작업은 먼저 지정된 요소를 저장소 대기열 store_queue에 대기열에 추가합니다. 마지막 요소를 제외한 모든 요소는 임시 대기열 temp_queue로 전송된 다음 저장 대기열 store_queue의 마지막 요소가 대기열에서 제거되어 반환됩니다. 구체적인 작업은 아래 그림과 같습니다. 🎜🎜🎜🎜🎜🎜[알고리즘]🎜🎜

算法运行过程需要始终保持其中一个队列为空，用作临时队列
入栈 push：在非空队列中插入元素 data。
若队列 queue_1 为空：
将 data 插入队列 queue_2 中
否则：
将 data 插入队列 queue_1 中
出栈 pop：将队列中的前 $n - 1$ 个元素插入另一队列，删除并返回最后一个元素
若队列 queue_1 不为空：
将队列 queue_1 的前 $n - 1$ 个元素插入 queue_2，然后 queue_1 的最后一个元素出队并返回
若队列 queue_2 不为空：
将队列 queue_2 的前 $n - 1$ 个元素插入 queue_1，然后 queue_2 的最后一个元素出队并返回

[代码]

class Stack:
    def __init__(self):
        self.queue_1 = Queue()
        self.queue_2 = Queue()
    def isempty(self):
        return self.queue_1.isempty() and self.queue_2.isempty()
    def push(self, data):
        if self.queue_2.isempty():
            self.queue_1.enqueue(data)
        else:
            self.queue_2.enqueue(data)
    def pop(self):
        if self.isempty():
            raise IndexError("Stack is empty")
        elif self.queue_2.isempty():
            while not self.queue_1.isempty():
                p = self.queue_1.dequeue()
                if self.queue_1.isempty():
                    return p
                self.queue_2.enqueue(p)
        else:
            while not self.queue_2.isempty():
                p = self.queue_2.dequeue()
                if self.queue_2.isempty():
                    return p
                self.queue_1.enqueue(p)

로그인 후 복사

[时空复杂度] push 操作的时间复杂度为 $O (1)$ ，由于 pop 操作时，都需要将所有元素从一个队列转移到另一队列，因此时间复杂度 $O (n)$ 。

3. 栈中元素连续性判断

[问题] 给定一栈 stack1，栈中元素均为整数，判断栈中每对连续的数字是否为连续整数(如果栈有奇数个元素，则排除栈顶元素)。例如，输入栈 [1, 2, 5, 6, -5, -4, 11, 10, 55]，输入为 True，因为排除栈顶元素 55 后，(1, 2)、(5, 6)、(-5, -4)、(11, 10) 均为连续整数。

[思路] 由于栈中可能存在奇数个元素，因此为了正确判断，首次需要将栈中元素反转，栈顶元素变为栈底，然后依次出栈，进行判断。

[算法]

栈 stack 中所有元素依次出栈，并插入队列 queue 中
队列 queue 中所有元素出队，并入栈 stack
while 栈 stack 不为空：
栈顶元素 e1 出栈，并插入队列 queue 中
如果栈 stack 不为空：
栈顶元素 e2 出栈，并插入队列 queue 中
如果 |e1-e2|!=1：
返回 False，跳出循环
队列 queue 中所有元素出队，并入栈 stack

[代码]

def check_stack_pair(stack):
    queue = Queue()
    flag = True
    # 反转栈中元素
    while not stack.isempty():
        queue.enqueue(stack.pop())
    while not queue.isempty():
        stack.push(queue.dequeue())
    while not stack.isempty():
        e1 = stack.pop()
        queue.enqueue(e1)
        if not stack.isempty():
            e2 = stack.pop()
            queue.enqueue(e2)
            if abs(e1-e2) != 1:
                flag = False
                break
    while not queue.isempty():
        stack.push(queue.dequeue())
    return flag

로그인 후 복사

[时空复杂度] 时间复杂度为 $O (n)$ ，空间复杂度为 $O (n)$ 。

4. 파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

[问题] 给定一个整数队列 queue，将队列的前半部分与队列的后半部分交错来重新排列元素。例如输入队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9]，则输出应为 [1, 6, 2, 7, 3, 8, 4, 9, 5]。

[思路] 通过获取队列的前半部分，然后利用栈的反转特性，可以实现重排操作，如下图所示：

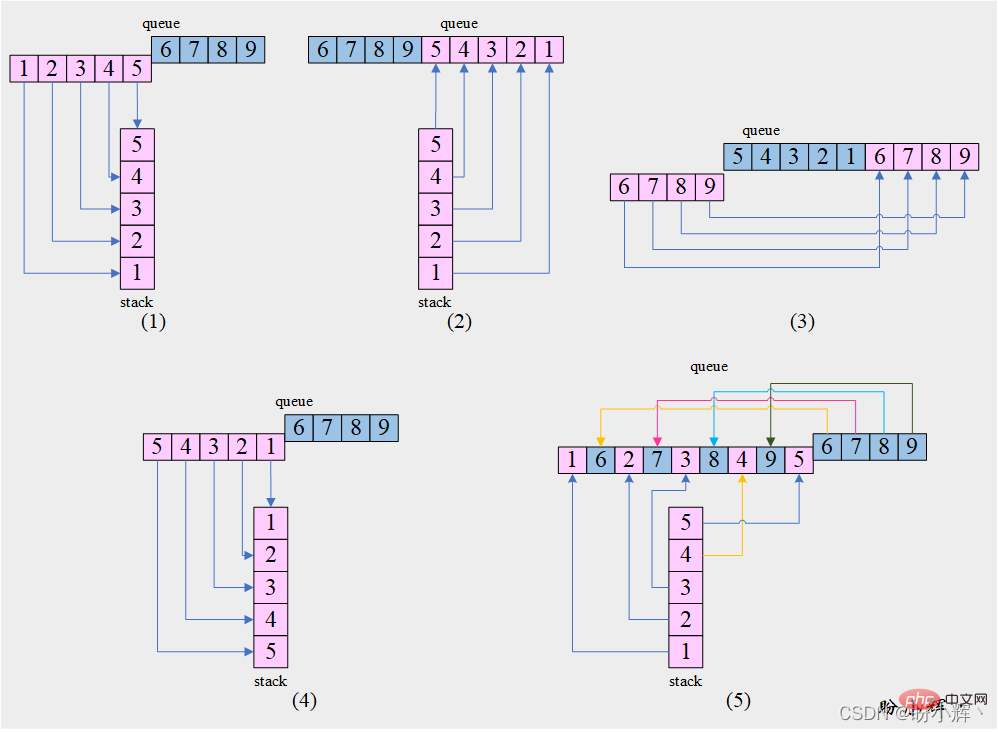
파이썬 큐 관련 애플리케이션과 실습을 함께 분석해 볼까요?

[算法]

如果队列 queue 中的元素数为偶数：
half=queue.size//2
否则：
half=queue.size//2+1
1. 将队列 queue 的前半部分元素依次出队并入栈 stack
2. 栈 stack 中元素出栈并入队 queue
3. 将队列 queue 中在步骤 1中未出队的另一部分元素依次出队并插入队尾
4. 将队列 queue 的前半部分元素依次出队并入栈 stack
5. 将栈 stack 和队列 queue 中的元素交替弹出并入队
6. 如果栈 stack 非空：
栈 stack 中元素出栈并入队

[代码]

def queue_order(queue):
    stack = Stack()
    size = queue.size    if size % 2 == 0:
        half = queue.size//2
    else:
        half = queue.size//2 + 1
    res = queue.size - half    for i in range(half):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(res):
        queue.enqueue(queue.dequeue())
    for i in range(half):
        stack.push(queue.dequeue())
    for i in range(res):
        queue.enqueue(stack.pop())
        queue.enqueue(queue.dequeue())
    if not stack.isempty():
        queue.enqueue(stack.pop())

로그인 후 복사

[时空复杂度] 时间复杂度为 $O (n)$ ，空间复杂度为 $O (n)$ 。

5. 反转队列中前 m 个元素的顺序

[问题] 给定一个整数 m 和一个整数队列 queue，反转队列中前 k 个元素的顺序，而其他元素保持不变。如 m=5，队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9]，算法输出为 [5, 4, 3, 2, 1, 6, 7, 8, 9]。

[思路] 结合 [问题4] 我们可以发现，此题就是 [问题4] 的前 3 步，如下图所示：

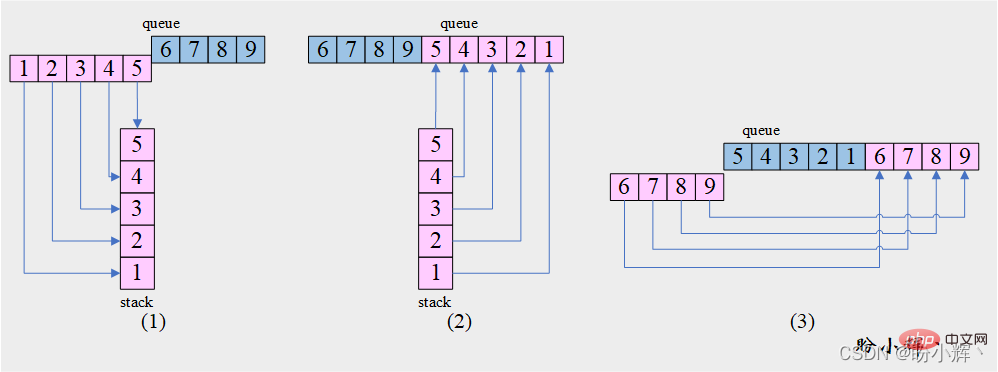
反转队列中前 m 个元素的顺序

[算法]

1. 将队列 queue 的前 m 个元素依次出队并入栈 stack
2. 栈 stack 中元素出栈并入队 queue
3. 将队列 queue 中在步骤 1中未出队的另一部分元素依次出队并插入队尾

[代码]

def reverse_m_element(queue, m):
    stack = Stack()
    size = queue.size    if queue.isempty() or m>size:
        return
    for i in range(m):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(size-m):
        queue.enqueue(queue.dequeue())

로그인 후 복사

[时空复杂度] 时间复杂度为 $O (n)$ ，空间复杂度为 $O (n)$ 。