이 글은 java에 대한 관련 지식을 제공합니다. 주로 이상한 점, 변화, 긴 정수 등을 포함한 언어 표현과 관련된 문제를 소개합니다. 모두에게 도움이 되기를 바랍니다.
추천 학습: "java 비디오 튜토리얼"
다음 방법은 유일한 매개변수가 홀수인지 확인하기 위한 것입니다. 이 방법이 올바르게 작동할 수 있나요?
public static boolean isOdd(int i){
returni%2==1:
}奇 奇은 2의 나머지 부분이 있는 정수로 정의될 수 있습니다. i%2라는 표현은 i를 2로 나눈 나머지를 계산하므로 이 프로그램이 올바르게 작동할 것 같습니다. 불행하게도 4분의 1의 확률로 잘못된 답을 반환할 수는 없습니다.
왜 분기인가요? 모든 int 값의 절반이 음수이고 isOdd 메서드는 모든 음수 홀수를 판단하지 못하기 때문입니다. 음의 정수에 대해 이 메서드를 호출하면 정수가 짝수인지 홀수인지에 관계없이 false가 반환됩니다. 이는 나머지 연산자(%)에 대한 Java 정의의 결과입니다. 이 연산자는 다음 상수 방정식을 충족하는 모든 int 값 A와 0이 아닌 모든 int 값 B로 정의됩니다.
(a/b)*b+(a%b)==a
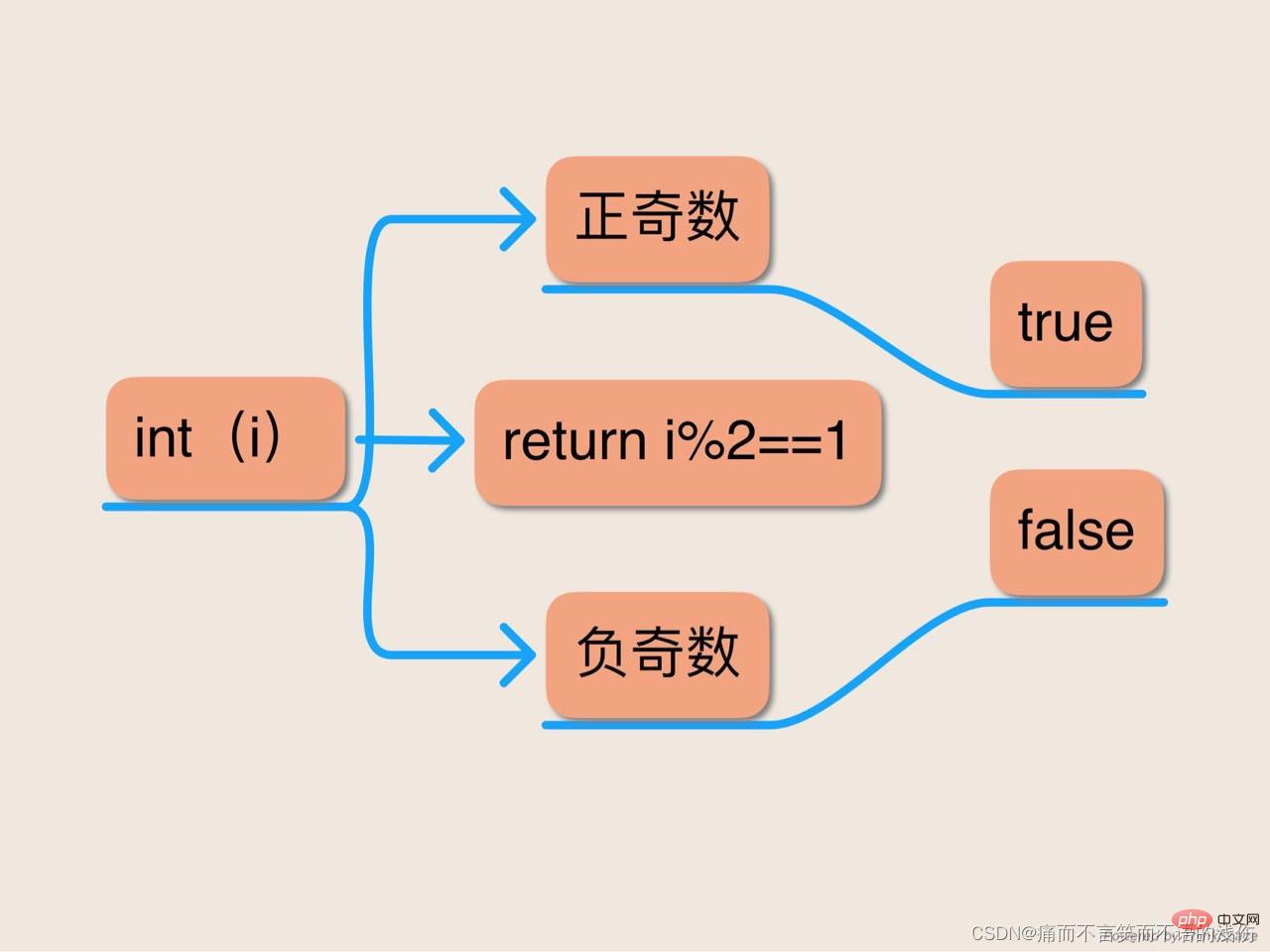
즉, B를 사용하여 A를 나누면 Shang을 곱합니다. B에 나머지를 더하면 원래 값 a를 얻습니다. 이 ID는 올바른 의미를 가지지만 Java의 잘린 정수 나누기 연산자와 결합하면 다음을 의미합니다. 나머지 연산이 0이 아닌 결과를 반환하는 경우 왼쪽 피연산자와 동일한 부호를 갖습니다.
i가 음수 홀수인 경우 i%2는 1이 아닌 -1이므로 isOdd 메서드는 false를 잘못 반환합니다. 이러한 예상치 못한 상황을 방지하려면 각 숫자 매개변수에 대해 음수, 0, 양수 값을 전달할 때 메서드가 올바르게 작동하는지 테스트하세요. 이 문제는 쉽게 해결됩니다. i%2를 1 대신 0과 비교하고 비교의 의미를 반대로 바꾸세요.
public static boolean isOdd(inti){
returni%2!=0;
}성능이 중요한 환경에서 isOdd 메서드를 사용하는 경우 비트 연산자 AND(&)를 사용하는 것이 더 나은 대안이 될 것입니다. 나머지 연산자:
public static boolean isOdd(inti){
return(i&1)!=0;
}즉, 나머지 연산자를 사용할 때마다 피연산자의 부호와 결과를 고려해야 합니다. 이 연산자의 동작은 피연산자가 음수가 아닐 때 자체 설명이 가능하지만, 피연산자 중 하나 또는 둘 다 음수인 경우에는 그렇지 않습니다
. 미스터리 2: 제로 순간 찾기
public class Change{
public static void main(String args[]){
Systemoutprintln(2.00-1.10);
}
}问题在于1.1这个数字不能被精确表示成为一个 double，因此它被表示成为最接近它的double值。该程序从2中减去的就是这个值。遗憾的是，这个计算的结果并不是最接近0.9的double值。表示结果的double值的最短表示就是你所看到的打印出来的那个可恶的数字。
更一般地说，问题在于并不是所有的小数都可以用二进制浮点数来精确表示的。
如果你正在用的是JDK5.0或更新的版本，那么你可能会受其诱惑，通过使用printf工具来设置输出精度的方订正该程序:
//拙劣的解决方案-仍旧是使用二进制浮点数
System.out.printf("%.2f%n",2.00-1.10);这条语句打印的是正确的结果，但是这并不表示它就是对底层问题的通用解决方案:它使用的仍日是二进制浮点数的double运算。浮点运算在一个范围很广的值域上提供了很好的近似，但是它通常不能产生精确的结果。二进制浮点对于货币计算是非常不适合的，因为它不可能将0.1-或者10的其它任何次负幂--精确表示为一个长度有限的二进制小数解决该问题的一种方式是使用某种整数类型，例如int或long，并且以分为单位来执行计算。如果你采纳了此路线，请确保该整数类型大到足够表示在程序中你将要用到的所有值。对这里举例的谜题来说，int就足够了。下面是我们用int类型来以分为单位表示货币值后重写的println语句。这个版本将打印出正确答案90分:
Systemoutprintln((200-110)+"cents")
解决该问题的另一种方式是使用执行精确小数运算的BigDecimal。它还可以通过JDBC与SQL DECIMAL类型进行互操作。这里要告诫你一点:一定要用BigDecimal(String)构造器，而千万不要用BigDecimal(double)。后一个构造器将用它的参数的精确”值来创建一个实例:new BigDecimal(1)将返回一个表示0100000000000000055511151231257827021181583404541015625BigDecimal。通过正确使用BigDecimal，程序就可以打印出我们所期望的结果0.90:
import java.math.BigDecimal;
public class Changel {
public static void main(String args[]){
System.out.println(newBigDecimal(2.00")
subtract(new BigDecimal("1.10")));
}
}这个版本并不是十分地完美，因为Java并没有为 BigDecimal提供任何语言上的支持。使用
BigDecimal的计算很有可能比那些使用原始类型的计算要慢一些，对某些大量使用小数计算的程序来说，这可能会成为问题，而对大多数程序来说，这显得一点也不重要。
总之，在需要精确答案的地方，要避免使用 float和double;对于货币计算，要使用int、long或BigDecimal。对于语言设计者来说，应该考虑对小数运算提供语言支持。一种方式是提供对操作符重载的有限支持，以使得运算符可以被塑造为能够对数值引用类型起作用，例如BigDecimal。另一种方式是提供原始的小数类型，就像COBOL与PL/I所作的一样。
这个谜题之所以被称为长整除是因为它所涉及的程序是有关两个long型数值整除的。被除数表示的是一天里的微秒数;而除数表示的是一天里的毫秒数。这个程序会打印出什么呢?
public class Longpision{
public static void main(String args[]){
final long MICROS PER DAY=24*60*60*1000*1000;
final long MILLIS PER DAY=24*60*60*1000;
Systemoutprintln(MICROS PER DAY/ MILLIS PER DAY);
}
}这个谜题看起来相当直观。每天的毫秒数和每天的微秒数都是常量。为清楚起见，它们都被表示成积的形式。每天的微秒数是(24小时/天*60分钟/小时*60秒/分钟*1000毫秒/秒*1000微秒/毫秒)。而每天的毫秒数的不同之处只是少了最后一个因子1000。当你用每天的毫秒数来整除每天的微秒数时，除数中所有的因子都被约掉了，只剩下1000，这正是每毫秒包含的微秒数。
除数和被除数都是long类型的，long类型大到了可以很容易地保存这两个乘积而不产生溢出。因此，看起来程序打印的必定是1000。遗憾的是，它打印的是5。这里到底发生了什么呢?
问题在于常数MICROS PER DAY的计算确实”溢出了。尽管计算的结果适合放入long中，并且其空间还有富余，但是这个结果并不适合放入 int中。这个计算完全是以int运算来执行的，并且只有在运算完成之后，其结果才被提升到long，而此时已经太迟了:计算已经溢出了，它返回的是一个小了200倍的数值。从int提升到 long是一种拓宽原始类型转换(widening primitive conversion)，它保留了(不正确的)数值。这个值之后被MILLIS PER DAY整除，而MILLIS PER DAY的计算是正确的，因为它适合int运算。这样整除的结果就得到了5。
那么为什么计算会是以int运算来执行的呢?为所有乘在一起的因子都是int数值。当你将两个int数值相乘时，你将得到另一个int数值。Java不具有目标确定类型的特性，这是一种语言特性，其含义是指存储结果的变量的类型会影响到计算所使用的类型。
通过使用long常量来替代int常量作为每一个乘积的第一个因子，我们就可以很容易地订正这个程序。这样做可以强制表达式中所有的后续计算都用long运作来完成。尽管这么做只在MICROS PER DAY表达式中是必需的，但是在两个乘积中都这么做是一种很好的方式。相似地，使用long作为乘积的“第一个”数值也并不总是必需的，但是这么做也是一种很好的形式。在两个计算中都以long数值开始可以很清楚地表明它们都不会溢出。下面的程序将打印出我们所期望的1000:
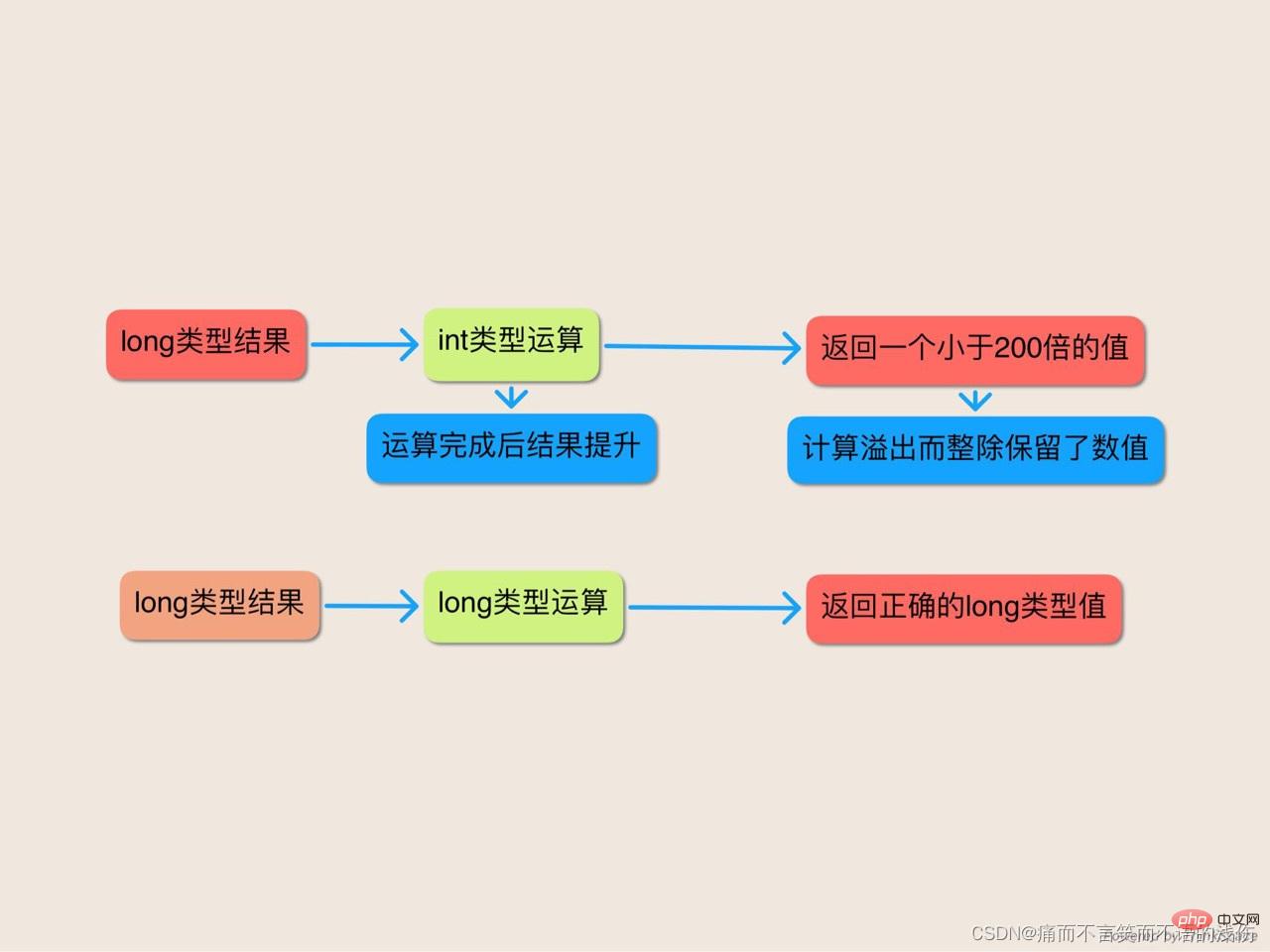
public class Longpision{
public static void main(String args[)
final long MICROS PER DAY=24L*60*60*1000*1000:
final long MILLIS PER DAY=24L*60*60*1000;
SystemoutprintlnMICROS PER DAY MILLIS PER DAY);
}
}这个教训很简单:当你在操作很大的数字时，千万要提防溢出--它可是一个缄默杀手。即使用来保存结果的变量已显得足够大，也并不意味着要产生结果的计算具有正确的类型。当你拿不准时，就使用long运算来执行整个计算。
语言设计者从中可以吸取的教训是:也许降低默溢出产生的可能性确实是值得做的一件事。这可以通过对不会产生缄默溢出的运算提供支持来实现。程序可以抛出一个异常而不是直接溢出。就像Ada所作的那样，或者它们可以在需要的时候自动地切换到一个更大的内部表示上以防止溢出，就像Lisp所作的那样。这两种方式都可能会遭受与其相关的性能方面的损失。降低缄默溢出的另一种方式是支持目标确定类型，但是这么做会显著地增加类型系统的复杂度。
得啦，前面那个谜题是有点棘手，但它是有关整除的，每个人都知道整除是很麻烦的。那么下面的程序只涉及加法，它又会打印出什么呢?
public class Elementary{
public static void main(String]args) {
Systemoutprintln(12345+54321);
}
}从表面上看，这像是一个很简单的谜题--简单到不需要纸和笔你就可以解决它。加号的左操作数的各个位是从1到5升序排列的，而右操作数是降序排列的。因此，相应各位的和仍然是常数，程序必定打印66666。对于这样的分析，只有一个问题:当你运行该程序时，它打印出的是17777。难道是Java对打印这样的非常数字抱有偏见吗?不知怎么的，这看起来并不像是一个合理的解释。
事物往往有别于它的表象。就以这个问题为例，它并没有打印出我们想要的输出。请仔细观察+操作符的两个操作数，我们是将一个int类型的12345加到了long类型的54321上。请注意左操作数开头的数字1和右操作数结尾的小写字母1之间的细微差异。数字1的水平笔划(称为“臂(arm)”)和垂直笔划(称为“茎(stem)”)之间是一个锐角，而与此相对照的是，小写字母l的臂和茎之间是一个直角。
在你大喊“恶心!”之前，你应该注意到这个问题确实已经引起了混乱，这里确实有一个教训:在 long型字面常量中，一定要用大写的L，千万不要用小写的1。这样就可以完全掐断这个谜题所产生的混乱的源头。
System.out.println(12345+5432L);
相类似的，要避免使用单独的一个1字母作为变量名。例如，我们很难通过观察下面的代码段来判断它到底是打印出列表1还是数字1。
List l=new ArrayList<string>() ;
l.add("Foo");
System.outprintln(1);</string>
总之，小写字母l和数字1在大多数打字机字体中都是几乎一样的。为避免你的程序的读者对二者产生混淆，千万不要使用小写的1来作为long型字面常量的结尾或是作为变量名。Java从C编程语言中继承良多，包括long型字面常量的语法。也许当初允许用小写的1来编写long型字面常量本身就是一个错误。
下面的程序是对两个十六进制(hex)字面常量进行相加，然后打印出十六进制的结果。这个程序会打印出什么呢?
public class JoyOfHex{
public static void main(String[] args){
System.out.println(
Long.toHexString(0x100000000L+0xcafebabe));
}
}看起来很明显，该程序应该打印出1cafebabe。毕竟，这确实就是十六进制数字10000000016与 cafebabe16的和。该程序使用的是long型运算，它可以支持16位十六进制数，因此运算溢出是不可能的。
然而，如果你运行该程序，你就会发现它打印出来的是cafebabe，并没有任何前导的1。这个输出表示的是正确结果的低32位，但是不知何故第33位丢失了。
看起来程序好像执行的是int型运算而不是long型运算，或者是忘了加第一个操作数。这里到底发生了什么呢?
十进制字面常量具有一个很好的属性，即所有的十进制字面常量都是正的，而十六进制和八进制字面常量并不具备这个属性。要想书写一个负的十进制常量，可以使用一元取反操作符(-)连接一个十进制字面常量。以这种方式，你可以用十进制来书写任何int或long型的数值，不管它是正的还是负的，并且负的十进制常数可以很明确地用一个减号符号来标识。但是十六进制和八进制字面常量并不是这么回事，它们可以具有正的以及负的数值。如果十六进制和八进制字面常量的最高位被置位了，那么它们就是负数。在这个程序中，数字Oxcafebabe是一个int常量，它的最高位被置位了，所以它是一个负数。它等于十进制数值-889275714。
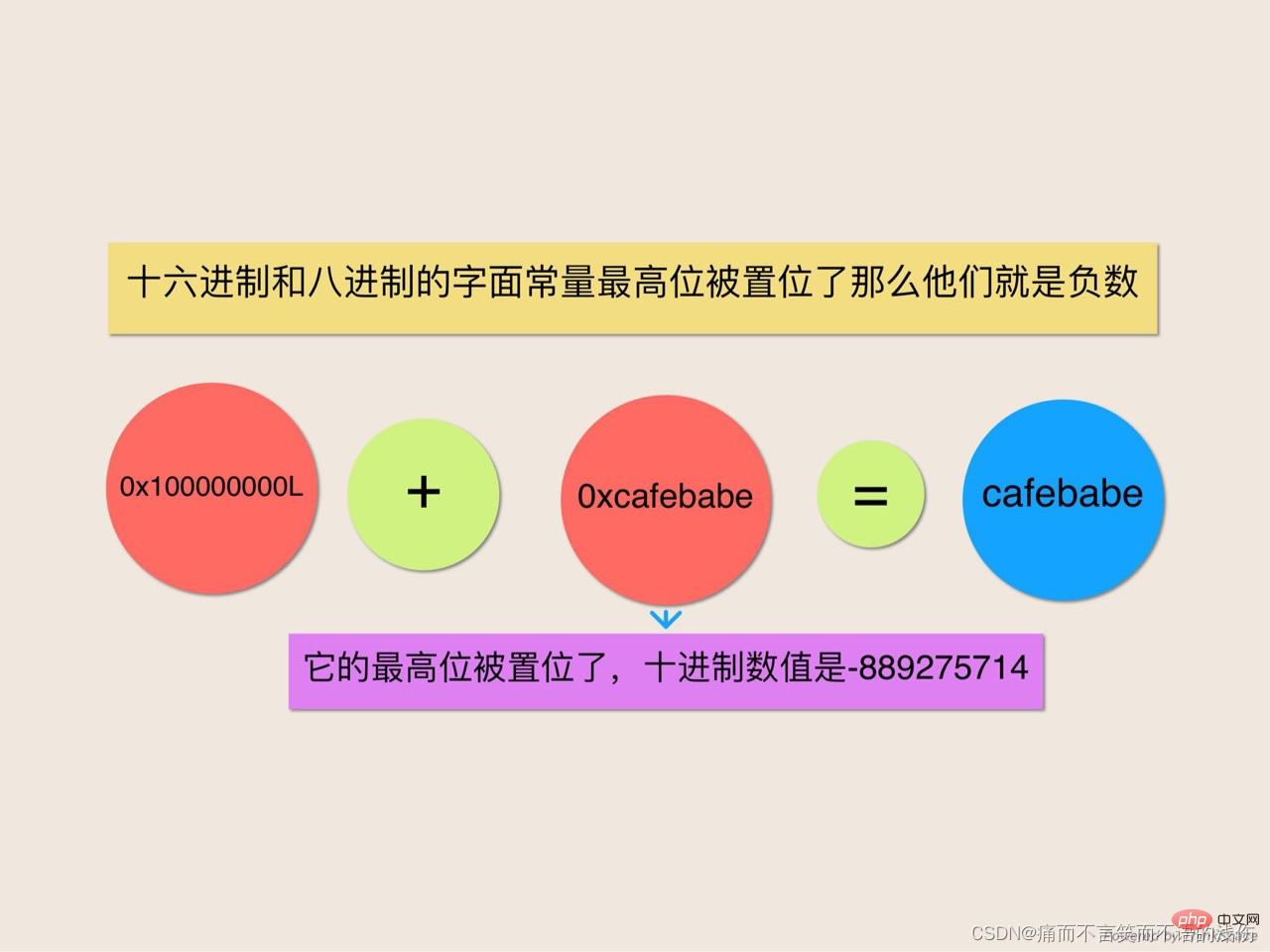
该程序执行的这个加法是一种“混合类型的计算(mixed-type computation)左操作数是long类型的，而右操作数是int类型的。为了执行该计算，Java将int类型的数值用拓宽原始类型转换提升为一个long类型，然后对两个long类型数值相加。因为int是一个有符号的整数类型，所以这个转换执行的是符合扩展:它将负的int类型的数值提升为一个在数值上相等的long类型数值。这个加法的右操作数0xcafebabe被提升为了long类型的数值0xffffffffcafebabeL。这个数值之后被加到了左操作数0x100000000L上。当作为int类型来被审视时，经过符号扩展之后的右操作数的高32位是-1，而左操作数的高32位是1，将这两个数相加就得到了0，这也就解释为什么在程序输出中前导1丢失了。下面所示是用手写的加法实现。(在加法上面的数字是进位。)
1111111 0xffffffffcafebabeL +0x0000000100000000L 0x00000000cafebabeL
订正该程序非常简单，只需用一个long十六进制字面常量来表示右操作数即可。这就可以避免了具有破坏力的符号扩展，并且程序也就可以打印出我们所期望的结果1cafebabe:
public class JoyOfHex{
public static void main(String[] args){
System.outprintln(
LongtoHexString(0x100000000L+0xcafebabeL));
}
}这个谜题给我们的教训是:混合类型的计算可能会产生混淆，尤其是十六进制和八进制字面常量无需显式的减号符号就可以表示负的数值。为了避免这种窘境，通常最好是避免混合类型的计算。对于语言的设计者们来说，应该考虑支持无符号的整数类型，从而根除符号扩展的可能性。可能会有这样的争辩:负的十六进制和八进制字面常量应该被禁用，但是这可能会挫伤程序员，他们经常使用十六进制字面常量来表示那些符号没有任何重要含义的数值。
推荐学习：《java视频教程》
위 내용은 Java 언어 표현에 관한 5가지 퍼즐 정리 및 공유의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![자바스크립트 심층 분석 [웹 프론트엔드의 기본은 알아야 한다]](https://img.php.cn/upload/course/000/000/041/61d3ff1c83b43350.jpg)
![TypeScript 소개 영상 [JavaScript를 배우지 않아도 이해할 수 있음]](https://img.php.cn/upload/course/000/000/068/6242c0fc4be39373.png)
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
