Java에서 이분법의 기본 아이디어와 구현을 간략하게 이해합니다.-java지도 시간-php.cn

이 기사에서는 java에 대한 관련 지식을 제공합니다. 이분법은 컴퓨터 검색 프로세스에서 자주 사용되는 매우 효율적인 알고리즘입니다. 다음에서는 이분법의 기본 아이디어와 구현을 예를 통해 자세히 설명하겠습니다. 모든 사람에게 도움이 되기를 바랍니다.

Java에서 이분법의 기본 아이디어와 구현을 간략하게 이해합니다.

추천 학습: "java 비디오 튜토리얼"

순서 배열에서 특정 숫자가 존재하는지 확인

아이디어:

순서 배열이므로 먼저 얻을 수 있습니다. 포인트 위치, 중간점은 배열을 왼쪽과 오른쪽 절반으로 나눌 수 있습니다.
중점 위치 값이 목표 값과 같을 경우 중간점 위치를 직접 반환합니다.
중간점 위치의 값이 목표값보다 작을 경우 배열의 중간점을 기준으로 왼쪽으로 가서 같은 방법으로 검색합니다.
중간점 위치의 값이 목표값보다 큰 경우 배열의 중간점의 오른쪽을 잡아 같은 방법으로 검색합니다.
끝까지 찾을 수 없으면 -1을 반환합니다.

Code

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

로그인 후 복사

시간 복잡도 O(logN). O(logN)。

在一个有序数组中，找大于等于某个数最左侧的位置

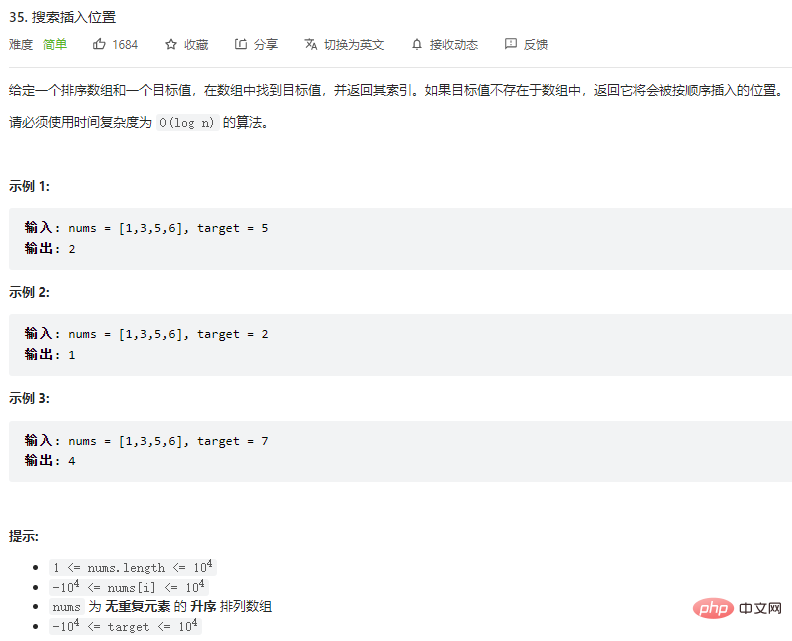
示例 1:

输入: nums = [1,3,5,6], target = 5

输出: 2

说明：如果要在num这个数组中插入 5 这个元素，应该是插入在元素 3 和元素 5 之间的位置，即 2 号位置。

示例 2:

输入: nums = [1,3,5,6], target = 2

输出: 1

说明：如果要在num这个数组中插入 2 这个元素，应该是插入在元素 1 和元素 3 之间的位置，即 1 号位置。

示例 3:

输入: nums = [1,3,5,6], target = 7

输出: 4

说明：如果要在num这个数组中插入 7 这个元素，应该是插入在数组末尾，即 4 号位置。

通过上述示例可以知道，这题本质上就是求在一个有序数组中，找大于等于某个数最左侧的位置，如果不存在，就返回数组长度（表示插入在最末尾位置）

我们只需要在上例基础上进行简单改动即可，上例中，我们找到满足条件的位置就直接return了

if (arr[m] == t) {
    return m;
}

로그인 후 복사

在本问题中，因为要找到最左侧的位置，所以，在遇到相等的时候，只需要先把位置记录下来，不用直接返回，然后继续去左侧找是否还有满足条件的更左边的位置。

同时，在遇到arr[m] > t条件下，也需要记录下此时的m位置，因为这也可能是满足条件的位置。

代码：

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

로그인 후 복사

整个算法的时间复杂度是O(logN)。

在排序数组中查找元素的第一个和最后一个位置

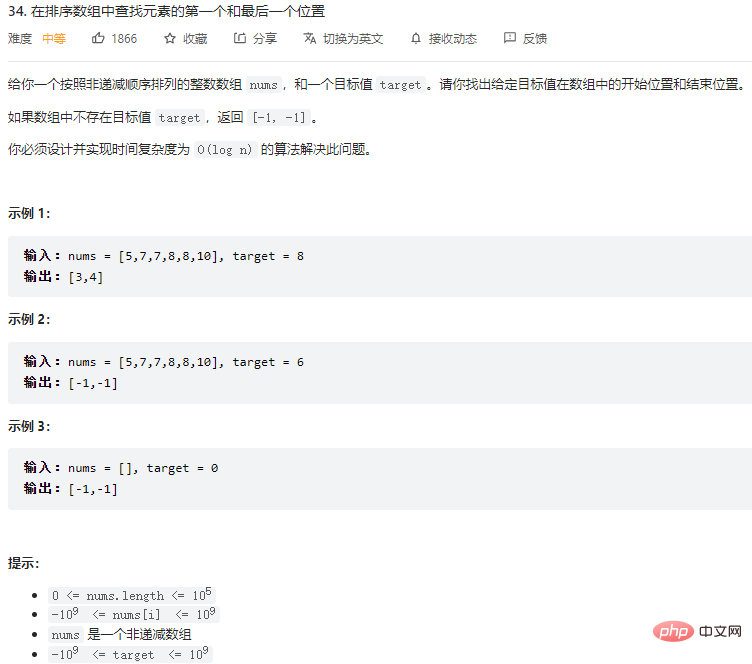
思路

本题也是用二分来解，当通过二分找到某个元素的时候，不急着返回，而是继续往左（右）找，看能否找到更左（右）位置匹配的值。

代码如下：

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

로그인 후 복사

时间复杂度 O(logN)。

局部最大值问题

思路

假设数组长度为N，首先判断0号位置的数和N-1位置的数是不是峰值位置。

0号位置只需要和1号位置比较，如果0号位置大，0号位置就是峰值位置，可以直接返回。

N-1号位置只需要和N-2号位置比较，如果N-1号位置大，N-1号位置就是峰值位置，可以直接返回。

如果0号位置和N-1在上轮比较中均是最小值，那么数组的样子必然是如下情况：

由上图可知，[0..1]区间内是增长趋势, [N-2...N-1]区间内是下降趋势。

那么峰值位置必在[1...N-2]之间出现。

此时可以通过二分来找峰值位置，先来到中点位置，假设为mid，如果中点位置的值比左右两边的值都大:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

로그인 후 복사

则mid

정렬된 배열에서 특정 숫자보다 크거나 같은 가장 왼쪽 위치를 찾습니다

예제 1:🎜🎜입력: nums = [1,3,5,6], target = 5🎜🎜출력: 2🎜🎜설명: num< /code>이 배열에 삽입된 요소 5는 요소 3과 요소 5 사이, 즉 위치 2에 삽입되어야 합니다. 🎜🎜예 2:🎜🎜입력: nums = [1,3,5,6], target = 2🎜🎜출력: 1🎜🎜설명: <code>num 배열에 2를 삽입하려는 경우 요소는 요소 1과 요소 3 사이, 즉 위치 1에 삽입되어야 합니다. 🎜🎜예 3:🎜🎜입력: nums = [1,3,5,6], target = 7🎜🎜출력: 4🎜🎜설명: num 배열에 7을 삽입하려는 경우 요소는 배열의 끝, 즉 위치 4에 삽입되어야 합니다. 🎜🎜위의 예를 보면 이 질문의 본질은 순서 배열에서 특정 숫자보다 크거나 같은 가장 왼쪽 위치를 찾는 것임을 알 수 있습니다. 존재하지 않으면 배열의 길이를 반환합니다(표시). 마지막 위치에 삽입됨)🎜🎜위 예시를 토대로 간단한 변경만 하면 됩니다. 위 예시에서는 조건에 맞는 위치를 찾으면 바로

return<을 합니다. /code>🎜public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}
로그인 후 복사
로그인 후 복사
🎜 이 질문에서는 가장 왼쪽 위치를 찾아야 하므로동등할 때 직접 반환하지 않고 먼저 위치만 기록한 다음 계속해서 왼쪽으로 이동하여 위치가 있는지 확인하면 됩니다. 조건을 충족하는 왼쪽 위치입니다. 🎜🎜동시에 arr[m] > t가 나타나면 m 위치도 기록해야 합니다. 조건을 만족하는 곳이기도 합니다. 🎜🎜코드: 🎜rrreee🎜전체 알고리즘의 시간 복잡도는 O(logN)입니다. 🎜🎜정렬된 배열에서 요소의 첫 번째 위치와 마지막 위치 찾기🎜🎜🎜🎜Thinking🎜🎜이 문제도 이진 나누기로 해결됩니다. 이진 나누기를 통해 요소를 찾았을 때, 서두르지 말고 계속해서 왼쪽(오른쪽)으로 검색하여 더 찾을 수 있는지 확인하세요. 왼쪽(오른쪽) ) 위치 일치 값. 🎜🎜코드는 다음과 같습니다: 🎜rrreee🎜시간 복잡도 O(logN). 🎜🎜로컬 최대 문제🎜🎜🎜🎜Ideas🎜🎜 가정 배열의 길이가 N인지 확인하려면 먼저 0 위치의 숫자와 N-1 위치의 숫자가 피크 위치인지 확인하세요. 🎜🎜0 위치는 1 위치와 비교하면 됩니다. 0 위치가 더 크면 0</ code> position 피크 위치이며 직접 반환될 수 있습니다. 🎜🎜<code>N-1 위치는 N-2 위치와 비교하면 됩니다. N-1 위치가 더 크면 < code>N Position -1

은 피크 위치이며 직접 반환될 수 있습니다. 🎜🎜마지막 비교 라운드에서 0 위치와 N-1이 모두 최소값인 경우 배열은 다음과 같아야 합니다. 🎜🎜

🎜🎜위 사진에서 알 수 있듯이 [ 0..1]</ code> 간격은 증가 추세이고, <code>[N-2...N-1] 간격은 감소 추세입니다. 🎜🎜그러면 피크 위치는 [1...N-2] 사이에 나타나야 합니다. 🎜🎜이때, 이등분을 통해 정점 위치를 찾을 수 있습니다. 먼저 중간점 위치의 값이 더 크다면 중간이라고 가정하고 중간점 위치로 이동합니다. 왼쪽과 오른쪽 값보다 :🎜rrreee🎜 mid 위치가 피크 위치로 바로 반환됩니다. 🎜🎜그렇지 않으면 다음 두 가지 상황이 있습니다. 🎜🎜사례 1: 중간 위치의 값이 중간 - 1 위치의 값보다 작습니다🎜

趋势如下图：

则在[1...(mid-1)]区间内继续二分。

情况二：mid 位置的值比 mid + 1 位置的值小

趋势是：

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

로그인 후 복사

时间复杂度O(logN)。

推荐学习：《java视频教程》

위 내용은 Java에서 이분법의 기본 아이디어와 구현을 간략하게 이해합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!