인과숲 알고리즘 기반 의사결정 측위 응용
Translator | Zhu Xianzhong
Reviewer | Sun Shujuan
이전블로그에서 원인과 결과를 사용하는 방법을 설명했습니다 나무를 정책의 이질적인 처리 효과 를 평가합니다. 아직 읽어보지 않으셨다면 이 글을 읽기 전에 읽어보시기를 권합니다. 왜냐하면 우리는 이 글을 생각 여러분이 의 을 이미 이해하고 있다고 생각하기 때문입니다. 이 기사와 관련된 일부 콘텐츠.
왜 이질적인 치료 효과(HTE: Heterogeneous Treatment Effects)인가요? 먼저, 이질적인 치료 효과 추정을 통해 치료 (약물, 광고, 제품 등)) 사용자(환자, 사용자, 고객 등)를 선택할 수 있습니다. 즉, HTE 가 우리의 타겟팅에 도움이 되는 것으로 추정됩니다. 실제로 기사 뒷부분의 에서 볼 수 있듯이 치료 접근 방식은 일부 사용자에게 긍정적인 이점을 제공하지만 평균적으로 비효과적이거나 심지어 비생산적일 수도 있습니다. 그 반대도 가능합니다. 약물은 평균적으로 효과적이지만 는 입니다. 사용자에 대한 정보를 명확하게 부작용이 있는 경우 , 이 약물의 효과 더 더 개선될 것입니다. 이 기사에서는 인과 나무의 확장인 인과 숲
숲을 살펴보겠습니다. 랜덤 포레스트가 여러 개의부트스트랩 트리를 함께 평균하여 회귀 트리를 확장하는 것처럼, 인과 포레스트도 인과 트리를 확장합니다. 가장 큰 차이점은 추론의 관점에서 비롯되는데, 이는 덜 간단합니다. 또한 다양한 HTE 추정 알고리즘의 결과를 비교하는 방법과 정책 목표에 사용하는 방법도 살펴보겠습니다. 온라인 할인 사례이 기사의 나머지 부분에서는
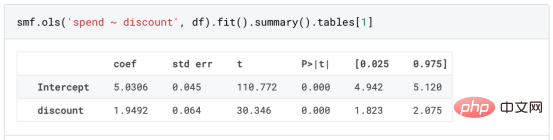
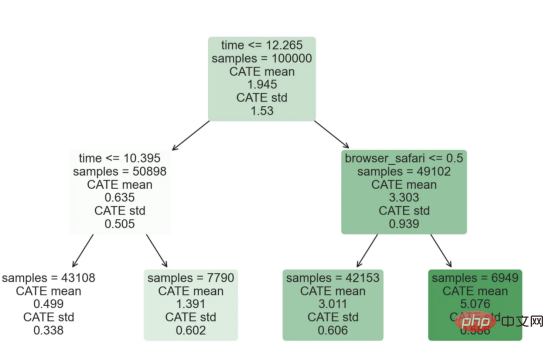
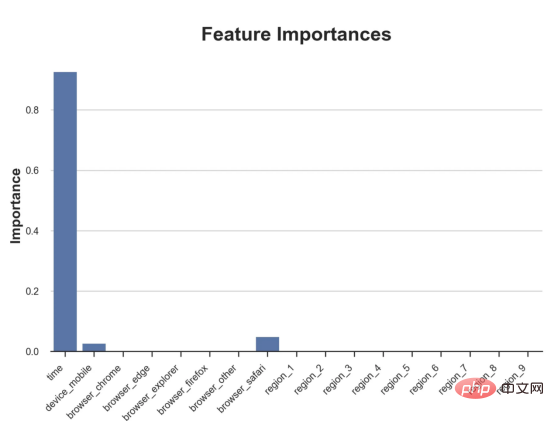
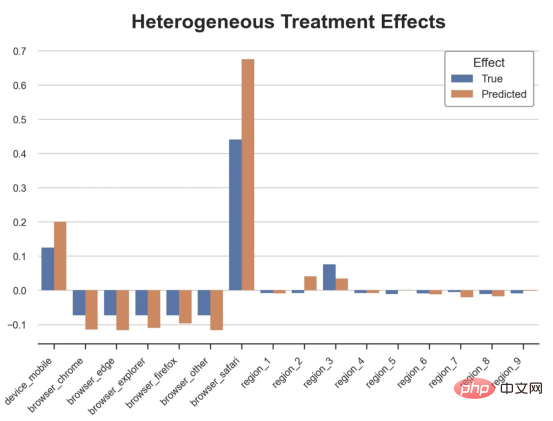
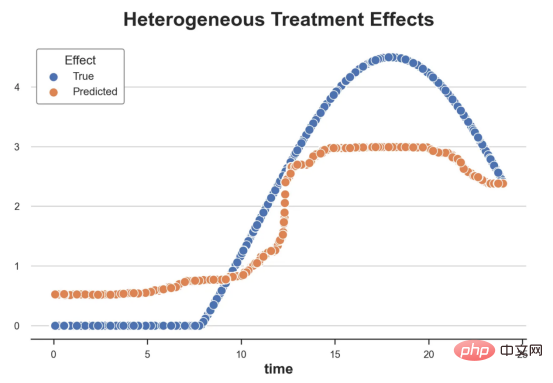
원인과 결과 트리에 관한 마지막 기사에서 사용된 장난감 예제를 계속 사용합니다. 원인과 결과 트리: 우리가 온라인 상점이고 우리는 신규 고객에게 할인을 제공하면 매장에서의 지출이 늘어나는지 알고 싶습니다.할인이 좋은지 확인하기 위해 다음과 같은 무작위 실험 또는 A/B 테스트를 수행했습니다. 신규 고객이 온라인 상점을 탐색할 때마다 무작위로 처리 조건에 할당합니다. 우리는 처리 대상인 사용자에게 할인 을 제공합니다. 제어 사용자에게는 할인을 제공하지 않습니다. 파일 src.dgp에서 데이터 생성 프로세스 dgp_online_discounts()을 가져옵니다. 또한 src.utilslibrary에서 일부 그리기 기능과 라이브러리를 가져옵니다. 코드뿐만 아니라 데이터와 테이블 및 기타 콘텐츠를 포함하기 위해 Web 기반의 Jupyter와 유사한 협업 노트북 환경인 Deepnote 프레임워크 를 사용했습니다. 우리는 100,000명의 온라인 cstore 방문자에 대한 데이터를 가지고 있으며 그들이 웹사이트를 방문하는 시간, 사용하는 장치, 사용하는 브라우저 및 지리적 지역을 관찰합니다. 우리는 또한 고객이 할인을 받았는지 여부, 할인을 처리한 방법 , 지출 금액 및 관심 있는 기타 결과 를 살펴봅니다. 실험이 무작위로 할당되므로 간단한 평균 차이 추정을 사용하여 실험 효과를 추정할 수 있습니다. 실험군은 할인을 제외하고는 대조군과 유사할 것으로 예상하므로 지출의 차이를 할인에 귀속시킬 수 있습니다. 할인 이 효과가 있는 것 같습니다. 실험 그룹의 평균 지출이 1.95달러 증가했습니다. 하지만 모든 고객이 똑같이 영향을 받나요? 이 질문에 답하기 위해 우리는 아마도 개인 수준에서 이질적인 치료 효과 를 추정하고 싶습니다. 이종 처리 효과를 계산하는 데는 다양한 옵션이 있습니다. 가장 간단한 접근 방식은 이질성 차원 측면에서 관심 결과와 상호 작용하는 것입니다. 이 접근 방식의 문제점은 어떤 변수를 선택할 것인가입니다. 때때로 우리는 우리의 행동을 미리 안내할 수 있는 정보를 가지고 있습니다 . 예를 들어 모바일 사용자가 데스크톱 사용자보다 평균적으로 더 많은 비용을 지출한다는 사실을 알 수 있습니다. 때로는 상업적인 이유로 특정 차원에 관심을 가질 수도 있습니다. 예를 들어 특정 지역에 더 많은 투자를 원할 수도 있습니다. 그러나 추가 정보가 없으면 프로세스가 데이터 기반이 되기를 원합니다. 이종 치료 효과 - 인과 관계 트리를 추정하기 위한 데이터 기반 접근 방식을 살펴봤습니다. 이제 이를 원인 숲으로 확장하겠습니다. 그러나 시작하기 전에 원인이 아닌 사촌인 랜덤 포레스트(Random Forest)를 소개해야 합니다. Random Forest는 이름에서 알 수 있듯이 회귀 트리의 확장으로 두 개의 독립적인 무작위 소스를 추가합니다. 특히, 랜덤 포레스트 알고리즘 은 데이터의 부트스트랩 샘플 으로 훈련된 다양한 회귀 트리에 대해 예측을 하고 이를 평균화할 수 있습니다. 이 프로세스는 종종 가이드 집계 알고리즘(배깅 알고리즘이라고도 함)이라고도 하며 모든 예측 알고리즘에 적용될 수 있으며 Random Forest에만 국한되지 않습니다. 무작위성의 추가 소스는 기능 선택에서 비롯됩니다. 각 분할에서 모든 기능 X의 무작위 하위 집합만 최적 분할을 위해 고려되기 때문입니다. 이 두 가지 추가 무작위성 소스는 매우 중요하며 Random Forest의 성능을 향상시키는 데 도움이 됩니다. 첫째, 배깅 알고리즘을 사용하면 랜덤 포레스트가 여러 이산 예측을 평균화하여 회귀 트리보다 더 부드러운 예측을 생성할 수 있습니다. 대조적으로, 무작위 특징 선택을 통해 무작위 포리스트는 특징 공간을 더 깊이 탐색할 수 있으므로 단순 회귀 트리보다 더 많은 상호 작용을 발견할 수 있습니다. 실제로 그 자체로는 그다지 예측력이 없지만(따라서 분열을 일으키지 않는) 변수 간에 상호 작용이 있을 수 있지만 함께 사용하면 매우 강력합니다. 원인 포리스트는 랜덤 포레스트와 동일하지만 인과 트리 및 회귀 트리와 마찬가지로 이종 처리 효과를 추정하는 데 사용됩니다. 인과 나무와 마찬가지로 우리에게는 기본적인 문제가 있습니다. 우리는 관찰하지 않은 개체, 즉 개별 치료 효과 τᵢ를 예측하는 데 관심이 있습니다. 해결책은 각 관찰에 대한 기대값이 정확히 치료 효과인 보조 결과 변수 Y*를 만드는 것입니다. 보조 결과 변수 이 변수가 개별 치료에 영향을 미치지 않는 이유에 대해 더 알고 싶다면 편견을 추가하는 경우 설정하고 싶어요 , 이전 글 을 봐주세요. 이번 글에서는 을 자세히 소개했습니다. 간단히 말해서 Yᵢ*를 단일 관찰에 대한 평균 차이 추정기로 생각할 수 있습니다. 결과 변수가 있으면 랜덤 포레스트를 사용하여 를 추정하기 위해 해야 할 일이 몇 가지 더 있습니다. 먼저, 각 리프에 동일한 수의 처리 장치와 제어 장치가 있는 트리를 구축해야 합니다. 둘째, 다양한 샘플을 사용하여 트리를 구축하고 평가해야 합니다. 즉, 각 리프의 평균 결과를 계산해야 합니다. 이 프로세스는 각 리프의 샘플을 트리 구조와 독립적으로 처리할 수 있으므로 추론에 매우 유용하므로 정직한 트리라고도 합니다. 평가를 진행하기 전에 범주형 변수 장치, 브라우저 지역에 대한 더미 변수를 생성해 보겠습니다. 를 추정할 수 있습니다. 다행히도 이 모든 작업을 수동으로 수행할 필요는 없습니다. 이미 Microsoft의 EconML 패키지에서 인과 트리 및 포리스트의 멋진 구현을 제공하고 있기 때문입니다. 의 CausalForestML 함수를 사용하겠습니다. 与因果树不同,因果森林更难解释,因为我们无法可视化每一棵树。我们可以使用SingleTreeateInterpreter函数来绘制因果森林算法的等效表示。 因果森林模型表示 我们可以像因果树模型一样解释树形图。在顶部,我们可以看到数据中的平均$Y^*$的值为1.917$。从那里开始,根据每个节点顶部突出显示的规则,数据被拆分为不同的分支。例如,根据时间是否晚于11.295,第一节点将数据分成大小为46878$和53122$的两组。在底部,我们得到了带有预测值的最终分区。例如,最左边的叶子包含40191$的观察值(时间早于11.295,在非Safari浏览器环境下),我们预测其花费为0.264$。较深的节点颜色表示预测值较高。 这种表示的问题在于,与因果树的情况不同,它只是对模型的解释。由于因果森林是由许多自助树组成的,因此无法直接检查每个决策树。了解在确定树分割时哪个特征最重要的一种方法是所谓的特征重要性。 显然,时间是异质性的第一个维度,其次是设备(特别是移动设备)和浏览器(特别是Safari)。其他维度无关紧要。 现在,让我们检查一下模型性能如何。 通常,我们无法直接评估模型性能,因为与标准的机器学习设置不同,我们没有观察到实际情况。因此,我们不能使用测试集来计算模型精度的度量。然而,在我们的案例中,我们控制了数据生成过程,因此我们可以获得基本的真相。让我们从分析模型如何沿着数据、设备、浏览器和区域的分类维度估计异质处理效应开始。 对于每个分类变量,我们绘制了实际和估计的平均处理效果。 作者提供的每个分类值的真实和估计处理效果 因果森林算法非常善于预测与分类变量相关的处理效果。至于因果树,这是预期的,因为算法具有非常离散的性质。然而,与因果树不同的是,预测更加微妙。 我们现在可以做一个更相关的测试:算法在时间等连续变量下的表现如何?首先,让我们再次隔离预测的处理效果,并忽略其他协变量。 def compute_time_effect(df, hte_model, avg_effect_notime): 我们现在可以复制之前的数字,但时间维度除外。我们绘制了一天中每个时间的平均真实和估计处理效果。 沿时间维度绘制的真实和估计的处理效果 我们现在可以充分理解因果树和森林之间的区别:虽然在因果树的情况下,估计基本上是一个非常粗略的阶跃函数,但我们现在可以看到因果树如何产生更平滑的估计。 我们现在已经探索了该模型,是时候使用它了! 假设我们正在考虑向访问我们在线商店的新客户提供4美元的折扣。 折扣对哪些客户有效?我们估计平均处理效果为1.9492美元。这意味着,平均而言折扣并不真正有利可图。然而,现在可以针对单个客户,我们只能向一部分新客户提供折扣。我们现在将探讨如何进行政策目标定位,为了更好地了解目标定位的质量,我们将使用因果树模型作为参考点。 我们使用相同的CauselForestML函数构建因果树,但将估计数和森林大小限制为1。 接下来,我们将数据集分成一个训练集和一个测试集。这一想法与交叉验证非常相似:我们使用训练集来训练模型——在我们的案例中是异质处理效应的估计器——并使用测试集来评估其质量。主要区别在于,我们没有观察到测试数据集中的真实结果。但是我们仍然可以使用训练测试分割来比较样本内预测和样本外预测。 我们将所有观察结果的80%放在训练集中,20%放在测试集中。 首先,让我们仅在训练样本上重新训练模型。 现在,我们可以确定目标策略,即决定我们向哪些客户提供折扣。答案似乎很简单:我们向所有预期处理效果大于成本(4美元)的客户提供折扣。 借助于一个可视化工具,它可以让我们了解处理对谁有效以及如何有效,这就是所谓的处理操作特征(TOC)曲线。这个名字可以看作是基于另一个更著名的接收器操作特性(ROC)曲线的修正,该曲线描绘了二元分类器的不同阈值的真阳性率与假阳性率。这两种曲线的想法类似:我们绘制不同比例受处理人群的平均处理效果。在一个极端情况下,当所有客户都被处理时,曲线的值等于平均处理效果;而在另一个极端情况下,当只有一个客户被处理时曲线的值则等于最大处理效果。 现在让我们计算曲线。 现在,我们可以绘制两个CATE估算器的处理操作特征(TOC)曲线。 处理操作特性曲线 正如预期的那样,两种估算器的TOC曲线都在下降,因为平均效应随着我们处理客户份额的增加而降低。换言之,我们在发布折扣时越有选择,每个客户的优惠券效果就越高。我还画了一条带有折扣成本的水平线,以便我们可以将TOC曲线下方和成本线上方的阴影区域解释为预期利润。 这两种算法预测的处理份额相似,约为20%,因果森林算法针对的客户略多一些。然而,他们预测的利润结果却大相径庭。因果树算法预测的边际较小且恒定,而因果林算法预测的是更大且更陡的边际。那么,哪一种算法更准确呢? 为了比较它们,我们可以在测试集中对它们进行评估。我们采用训练集上训练的模型,预测处理效果,并将其与测试集上训练模型的预测进行比较。注意,与机器学习标准测试程序不同,有一个实质性的区别:在我们的案例中,我们无法根据实际情况评估我们的预测,因为没有观察到处理效果。我们只能将两个预测相互比较。 因果树模型似乎比因果森林模型表现得更好一些,总净效应为8386美元——相对于4948美元。从图中,我们也可以了解差异的来源。因果森林算法往往限制性更强,处理的客户更少,没有误报的阳性,但也有很多误报的阴性。另一方面,因果树算法看起来更加“慷慨”,并将折扣分配给更多的新客户。这既转化为更多的真阳性,也转化为假阳性。总之,净效应似乎有利于因果树算法。 通常,我们讨论到这里就可以停止了,因为我们可以做的事情不多了。然而,在我们的案例情形中,我们还可以访问真正的数据生成过程。因此,接下来我们不妨检查一下这两种算法的真实精度。 首先,让我们根据处理效果的预测误差来比较它们。对于每个算法,我们计算处理效果的均方误差。 结果是,随机森林模型更好地预测了平均处理效果,均方误差为0.5555美元,而不是0.9035美元。 那么,这是否意味着更好的目标定位呢?我们现在可以复制上面所做的相同的柱状图,以了解这两种算法在策略目标方面的表现。 这两幅图非常相似,但结果却大相径庭。事实上,因果森林算法现在优于因果树算法,总效果为10395美元,而非8828美元。为什么会出现这种突然的差异呢? 为了更好地理解差异的来源,让我们根据实际情况绘制TOC。 处理操作特性曲线。 正如我们所看到的,TOC是倾斜度非常大的,存在一些平均处理效果非常高的客户。随机森林算法能够更好地识别它们,因此总体上更有效,尽管目标客户较少些。 이 기사에서 우리는 이종 처리 효과의 알고리즘에 대한 함수 매우 강력한 추정을 배웠습니다— 인과의 숲. 인과 포리스트는 인과 트리와 동일한 원칙을 기반으로 구축되었지만 매개변수 공간과 배깅 알고리즘 에 대한 더 깊은 탐색의 이점을 누릴 수 있습니다. ㅋㅋㅋ 가장 높은 치료 정책의 수익성을 보장할 수 있습니다. 또한 분포의 꼬리가 평균보다 더 강한 상관을 가질 수 있기 때문에 정책 목표가 이종 치료 효과를 추정하는 목표와 다르다는 것을 알 수 있습니다. 참고자료S. Athey, G. Imbens, 이종 인과 효과를 위한 재귀 분할(2016), Athey, J. Tibshirani, S. Wager, Generalized Random Forests(2019). 통계 연대기. OPRESCU, v. Syritkanis, Z. Wu, 인과 추론을 위한 직교 무작위 숲(2019). 기계 학습에 관한 제36차 국제 컨퍼런스 진행. 번역가 소개Zhu Xianzhong, 51CTO 커뮤니티 편집자 51CTO 전문 블로거, 강사, 웨이팡 대학의 컴퓨터 교사이자 프리랜스 프로그래밍 업계의 베테랑입니다. 제목: From Causal Trees to Forests , 저자: Matteo Courthoud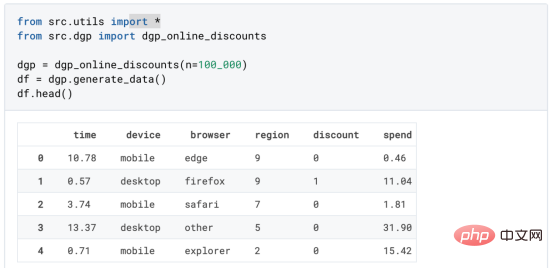
인과의 숲
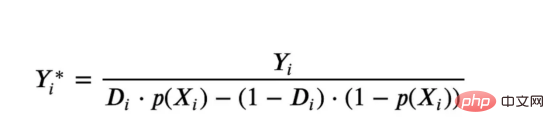
df_dummies = pd.get_dummies(df[dgp.X[1:]], drop_first=True)
df = pd.concat([df, df_dummies], axis=1)
X = ['time'] + list(df_dummies.columns)
from econml.dml import CausalForestDML
np.random.seed(0)
forest_model = CausalForestDML(max_depth=3)
forest_model = forest_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
from econml.cate_interpreter import SingleTreeCateInterpreter
intrp = SingleTreeCateInterpreter(max_depth=2).interpret(forest_model, df[X])
intrp.plot(feature_names=X, fnotallow=12)

性能
def compute_discrete_effects(df, hte_model):
temp_df = df.copy()
temp_df.time = 0
temp_df = dgp.add_treatment_effect(temp_df)
temp_df = temp_df.rename(columns={'effect_on_spend': 'True'})
temp_df['Predicted'] = hte_model.effect(temp_df[X])
df_effects = pd.DataFrame()
for var in X[1:]:
for effect in ['True', 'Predicted']:
v = temp_df.loc[temp_df[var]==1, effect].mean() - temp_df[effect][temp_df[var]==0].mean()
effect_var = {'Variable': [var], 'Effect': [effect], 'Value': [v]}
df_effects = pd.concat([df_effects, pd.DataFrame(effect_var)]).reset_index(drop=True)
return df_effects, temp_df['Predicted'].mean()
df_effects, avg_effect_notime = compute_discrete_effects(df, forest_model)fig, ax = plt.subplots()
sns.barplot(data=df_effects, x="Variable", y="Value", hue="Effect", ax=ax).set(
xlabel='', ylabel='', title='Heterogeneous Treatment Effects')
ax.set_xticklabels(ax.get_xticklabels(), rotatinotallow=45, ha="right");
df_time = df.copy()
df_time[[X[1:]] + ['device', 'browser', 'region']] = 0
df_time = dgp.add_treatment_effect(df_time)
df_time['predicted'] = hte_model.effect(df_time[X]) + avg_effect_notime
return df_time
df_time = compute_time_effect(df, forest_model, avg_effect_notime)
sns.scatterplot(x='time', y='effect_on_spend', data=df_time, label='True')
sns.scatterplot(x='time', y='predicted', data=df_time, label='Predicted').set(
ylabel='', title='Heterogeneous Treatment Effects')
plt.legend(title='Effect');
策略定位
cost = 4
from econml.dml import CausalForestDML
np.random.seed(0)
tree_model = CausalForestDML(n_estimators=1, subforest_size=1, inference=False, max_depth=3)
tree_model = tree_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
df_train, df_test = df.iloc[:80_000, :], df.iloc[20_000:,]
np.random.seed(0)
tree_model = tree_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
forest_model = forest_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
def compute_toc(df, hte_model, cost, truth=False):
df_toc = pd.DataFrame()
for q in np.linspace(0, 1, 101):
if truth:
df = dgp.add_treatment_effect(df_test)
effect = df['effect_on_spend']
else:
effect = hte_model.effect(df[X])
ate = np.mean(effect[effect >= np.quantile(effect, 1-q)])
temp = pd.DataFrame({'q': [q], 'ate': [ate]})
df_toc = pd.concat([df_toc, temp]).reset_index(drop=True)
return df_toc
df_toc_tree = compute_toc(df_train, tree_model, cost)
df_toc_forest = compute_toc(df_train, forest_model, cost)def plot_toc(df_toc, cost, ax, color, title):
ax.axhline(y=cost, lw=2, c='k')
ax.fill_between(x=df_toc.q, y1=cost, y2=df_toc.ate, where=(df_toc.ate > cost), color=color, alpha=0.3)
if any(df_toc.ate > cost):
q = df_toc_tree.loc[df_toc.ate > cost, 'q'].values[-1]
else:
q = 0
ax.axvline(x=q, ymin=0, ymax=0.36, lw=2, c='k', ls='--')
sns.lineplot(data=df_toc, x='q', y='ate', ax=ax, color=color).set(
title=title, ylabel='ATT', xlabel='Share of treated', ylim=[1.5, 8.5])
ax.text(0.7, cost+0.1, f'Discount cost: {cost:.0f}$', fnotallow=12)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
plot_toc(df_toc_tree, cost, ax1, 'C0', 'TOC - Causal Tree')
plot_toc(df_toc_forest, cost, ax2, 'C1', 'TOC - Causal Forest')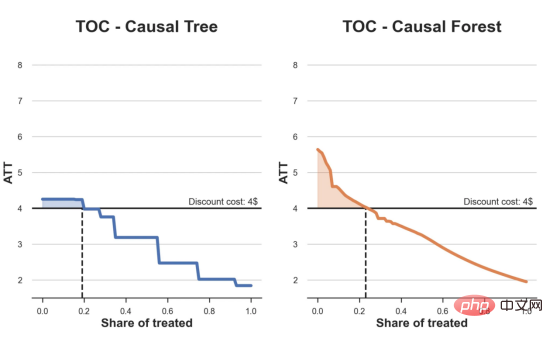
def compute_effect_test(df_test, hte_model, cost, ax, title, truth=False):
df_test['Treated'] = hte_model.effect(df_test[X]) > cost
if truth:
df_test = dgp.add_treatment_effect(df_test)
df_test['Effect'] = df_test['effect_on_spend']
else:
np.random.seed(0)
hte_model_test = copy.deepcopy(hte_model).fit(Y=df_test[dgp.Y], X=df_test[X], T=df_test[dgp.D])
df_test['Effect'] = hte_model_test.effect(df_test[X])
df_test['Cost Effective'] = df_test['Effect'] > cost
tot_effect = ((df_test['Effect'] - cost) * df_test['Treated']).sum()
sns.barplot(data=df_test, x='Cost Effective', y='Treated', errorbar=None, width=0.5, ax=ax, palette=['C3', 'C2']).set(
title=title + 'n', ylim=[0,1])
ax.text(0.5, 1.08, f'Total effect: {tot_effect:.2f}', fnotallow=14, ha='center')
return
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree')
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest')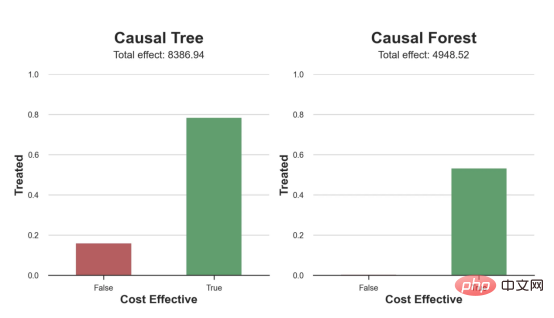
from sklearn.metrics import mean_squared_error as mse
def compute_mse_test(df_test, hte_model):
df_test = dgp.add_treatment_effect(df_test)
print(f"MSE = {mse(df_test['effect_on_spend'], hte_model.effect(df_test[X])):.4f}")
compute_mse_test(df_test, tree_model)
compute_mse_test(df_test, forest_model)fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree', True)
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest', True)
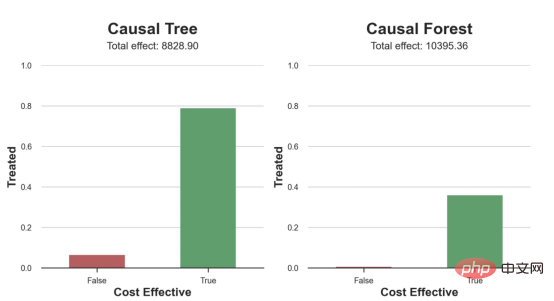
df_toc = compute_toc(df_test, tree_model, cost, True)
fix, ax = plt.subplots(1, 1, figsize=(7, 5))
plot_toc(df_toc, cost, ax, 'C2', 'TOC - Ground Truth')
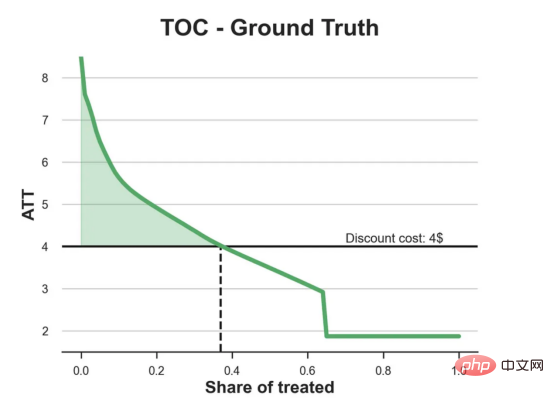
결론
위 내용은 인과숲 알고리즘 기반 의사결정 측위 응용의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)
 이 기사에서는 SHAP: 기계 학습을 위한 모델 설명을 이해하도록 안내합니다.
Jun 01, 2024 am 10:58 AM
이 기사에서는 SHAP: 기계 학습을 위한 모델 설명을 이해하도록 안내합니다.
Jun 01, 2024 am 10:58 AM
기계 학습 및 데이터 과학 분야에서 모델 해석 가능성은 항상 연구자와 실무자의 초점이었습니다. 딥러닝, 앙상블 방법 등 복잡한 모델이 널리 적용되면서 모델의 의사결정 과정을 이해하는 것이 특히 중요해졌습니다. explainable AI|XAI는 모델의 투명성을 높여 머신러닝 모델에 대한 신뢰와 확신을 구축하는 데 도움이 됩니다. 모델 투명성을 향상시키는 것은 여러 복잡한 모델의 광범위한 사용은 물론 모델을 설명하는 데 사용되는 의사 결정 프로세스와 같은 방법을 통해 달성할 수 있습니다. 이러한 방법에는 기능 중요도 분석, 모델 예측 간격 추정, 로컬 해석 가능성 알고리즘 등이 포함됩니다. 특성 중요도 분석은 모델이 입력 특성에 미치는 영향 정도를 평가하여 모델의 의사결정 과정을 설명할 수 있습니다. 모델 예측 구간 추정
 C++에서 기계 학습 알고리즘 구현: 일반적인 과제 및 솔루션
Jun 03, 2024 pm 01:25 PM
C++에서 기계 학습 알고리즘 구현: 일반적인 과제 및 솔루션
Jun 03, 2024 pm 01:25 PM
C++의 기계 학습 알고리즘이 직면하는 일반적인 과제에는 메모리 관리, 멀티스레딩, 성능 최적화 및 유지 관리 가능성이 포함됩니다. 솔루션에는 스마트 포인터, 최신 스레딩 라이브러리, SIMD 지침 및 타사 라이브러리 사용은 물론 코딩 스타일 지침 준수 및 자동화 도구 사용이 포함됩니다. 실제 사례에서는 Eigen 라이브러리를 사용하여 선형 회귀 알고리즘을 구현하고 메모리를 효과적으로 관리하며 고성능 행렬 연산을 사용하는 방법을 보여줍니다.
 당신이 모르는 머신러닝의 5가지 학교
Jun 05, 2024 pm 08:51 PM
당신이 모르는 머신러닝의 5가지 학교
Jun 05, 2024 pm 08:51 PM
머신 러닝은 명시적으로 프로그래밍하지 않고도 컴퓨터가 데이터로부터 학습하고 능력을 향상시킬 수 있는 능력을 제공하는 인공 지능의 중요한 분야입니다. 머신러닝은 이미지 인식, 자연어 처리, 추천 시스템, 사기 탐지 등 다양한 분야에서 폭넓게 활용되며 우리의 삶의 방식을 변화시키고 있습니다. 기계 학습 분야에는 다양한 방법과 이론이 있으며, 그 중 가장 영향력 있는 5가지 방법을 "기계 학습의 5개 학교"라고 합니다. 5개 주요 학파는 상징학파, 연결주의 학파, 진화학파, 베이지안 학파, 유추학파이다. 1. 상징주의라고도 알려진 상징주의는 논리적 추론과 지식 표현을 위해 상징을 사용하는 것을 강조합니다. 이 사고 학교는 학습이 기존을 통한 역연역 과정이라고 믿습니다.
 Flash Attention은 안정적인가요? Meta와 Harvard는 모델 중량 편차가 수십 배로 변동한다는 사실을 발견했습니다.
May 30, 2024 pm 01:24 PM
Flash Attention은 안정적인가요? Meta와 Harvard는 모델 중량 편차가 수십 배로 변동한다는 사실을 발견했습니다.
May 30, 2024 pm 01:24 PM
MetaFAIR는 대규모 기계 학습을 수행할 때 생성되는 데이터 편향을 최적화하기 위한 새로운 연구 프레임워크를 제공하기 위해 Harvard와 협력했습니다. 대규모 언어 모델을 훈련하는 데는 수개월이 걸리고 수백 또는 수천 개의 GPU를 사용하는 것으로 알려져 있습니다. LLaMA270B 모델을 예로 들면, 훈련에는 총 1,720,320 GPU 시간이 필요합니다. 대규모 모델을 교육하면 이러한 워크로드의 규모와 복잡성으로 인해 고유한 체계적 문제가 발생합니다. 최근 많은 기관에서 SOTA 생성 AI 모델을 훈련할 때 훈련 프로세스의 불안정성을 보고했습니다. 이는 일반적으로 손실 급증의 형태로 나타납니다. 예를 들어 Google의 PaLM 모델은 훈련 과정에서 최대 20번의 손실 급증을 경험했습니다. 수치 편향은 이러한 훈련 부정확성의 근본 원인입니다.
 설명 가능한 AI: 복잡한 AI/ML 모델 설명
Jun 03, 2024 pm 10:08 PM
설명 가능한 AI: 복잡한 AI/ML 모델 설명
Jun 03, 2024 pm 10:08 PM
번역기 | 검토자: Li Rui | Chonglou 인공 지능(AI) 및 기계 학습(ML) 모델은 오늘날 점점 더 복잡해지고 있으며 이러한 모델에서 생성되는 출력은 이해관계자에게 설명할 수 없는 블랙박스입니다. XAI(Explainable AI)는 이해관계자가 이러한 모델의 작동 방식을 이해할 수 있도록 하고, 이러한 모델이 실제로 의사 결정을 내리는 방식을 이해하도록 하며, AI 시스템의 투명성, 이 문제를 해결하기 위한 신뢰 및 책임을 보장함으로써 이 문제를 해결하는 것을 목표로 합니다. 이 기사에서는 기본 원리를 설명하기 위해 다양한 설명 가능한 인공 지능(XAI) 기술을 살펴봅니다. 설명 가능한 AI가 중요한 몇 가지 이유 신뢰와 투명성: AI 시스템이 널리 수용되고 신뢰되려면 사용자가 의사 결정 방법을 이해해야 합니다.
 탐지 알고리즘 개선: 고해상도 광학 원격탐사 이미지에서 표적 탐지용
Jun 06, 2024 pm 12:33 PM
탐지 알고리즘 개선: 고해상도 광학 원격탐사 이미지에서 표적 탐지용
Jun 06, 2024 pm 12:33 PM
01 전망 요약 현재로서는 탐지 효율성과 탐지 결과 간의 적절한 균형을 이루기가 어렵습니다. 우리는 광학 원격 탐사 이미지에서 표적 감지 네트워크의 효과를 향상시키기 위해 다층 특징 피라미드, 다중 감지 헤드 전략 및 하이브리드 주의 모듈을 사용하여 고해상도 광학 원격 감지 이미지에서 표적 감지를 위한 향상된 YOLOv5 알고리즘을 개발했습니다. SIMD 데이터 세트에 따르면 새로운 알고리즘의 mAP는 YOLOv5보다 2.2%, YOLOX보다 8.48% 우수하여 탐지 결과와 속도 간의 균형이 더 잘 이루어졌습니다. 02 배경 및 동기 원격탐사 기술의 급속한 발전으로 항공기, 자동차, 건물 등 지구 표면의 많은 물체를 묘사하기 위해 고해상도 광학 원격탐사 영상이 활용되고 있다. 원격탐사 이미지 해석에서 물체 감지
 C++의 기계 학습: C++의 일반적인 기계 학습 알고리즘 구현 가이드
Jun 03, 2024 pm 07:33 PM
C++의 기계 학습: C++의 일반적인 기계 학습 알고리즘 구현 가이드
Jun 03, 2024 pm 07:33 PM
C++에서 기계 학습 알고리즘의 구현에는 다음이 포함됩니다. 선형 회귀: 연속 변수를 예측하는 데 사용됩니다. 단계에는 데이터 로드, 가중치 및 편향 계산, 매개변수 업데이트 및 예측이 포함됩니다. 로지스틱 회귀: 이산형 변수를 예측하는 데 사용됩니다. 이 프로세스는 선형 회귀와 유사하지만 예측에 시그모이드 함수를 사용합니다. 지원 벡터 머신(Support Vector Machine): 지원 벡터 계산 및 레이블 예측을 포함하는 강력한 분류 및 회귀 알고리즘입니다.
 58 초상화 플랫폼 구축에 알고리즘 적용
May 09, 2024 am 09:01 AM
58 초상화 플랫폼 구축에 알고리즘 적용
May 09, 2024 am 09:01 AM
1. 58초상화 플랫폼 구축 배경 먼저, 58초상화 플랫폼 구축 배경에 대해 말씀드리겠습니다. 1. 기존 프로파일링 플랫폼의 전통적인 사고로는 더 이상 충분하지 않습니다. 사용자 프로파일링 플랫폼을 구축하려면 여러 비즈니스 라인의 데이터를 통합하여 정확한 사용자 초상화를 구축하는 데이터 웨어하우스 모델링 기능이 필요합니다. 그리고 알고리즘 측면의 기능을 제공해야 하며, 마지막으로 사용자 프로필 데이터를 효율적으로 저장, 쿼리 및 공유하고 프로필 서비스를 제공할 수 있는 데이터 플랫폼 기능도 있어야 합니다. 자체 구축한 비즈니스 프로파일링 플랫폼과 중간 사무실 프로파일링 플랫폼의 주요 차이점은 자체 구축한 프로파일링 플랫폼이 단일 비즈니스 라인에 서비스를 제공하고 필요에 따라 사용자 정의할 수 있다는 것입니다. 모델링하고 보다 일반적인 기능을 제공합니다. 2.58 Zhongtai 초상화 구성 배경의 사용자 초상화






